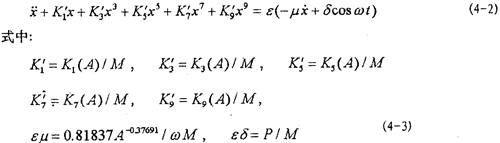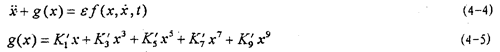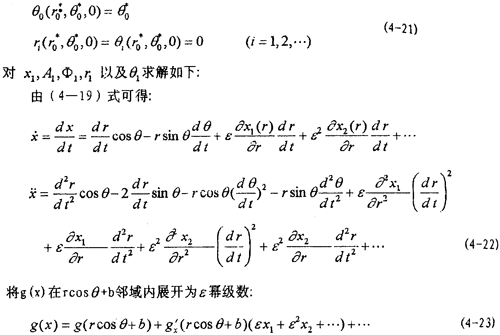第四章 強(qiáng)非線性系統(tǒng)的頻閃—諧波平衡法
4-1 引言
在探索具有非線性遲滯特性元件的系統(tǒng)在簡諧激勵下穩(wěn)態(tài)響應(yīng)的求解方法時码邻,我們擬研究以下系統(tǒng):
M +
+ (x滓层,
(x滓层,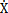 庐舟,A丰浙,ω)=Pcosωt (4-1)
庐舟,A丰浙,ω)=Pcosωt (4-1)
式中M為系統(tǒng)質(zhì)量,P為激勵力幅值,ω為激勵園頻率 (x,
(x,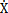 董记,A,ω)=
董记,A,ω)= 1(A赐赁,x)+
1(A赐赁,x)+ 2(A檀塌,ω,
2(A檀塌,ω,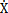 )雕踊,
)雕踊, 1和
1和 2分別為上章中的(3-12)和(3-41)式前河。為研究方便,將(3-12)和(3-41)式代入(4-1)式并改寫成以下形式:
2分別為上章中的(3-12)和(3-41)式前河。為研究方便,將(3-12)和(3-41)式代入(4-1)式并改寫成以下形式:
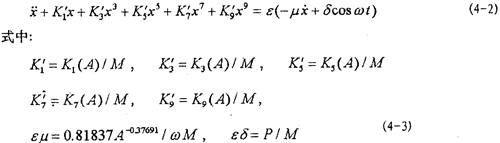
式中K1(A)挺候,K3(A)框嫁,K5(A),K7(A)即钞,K9(A)為(3-27)式形炬。由式(4-2)可知,這一系統(tǒng)是一個強(qiáng)非線性非自治系統(tǒng)部爱。
目前文獻(xiàn)上的一些方法對于弱非線性系統(tǒng)是有效的亏吝,而對于(4-2)式的強(qiáng)非線性系統(tǒng)則遇到了麻煩。由于描述非線性振動系統(tǒng)的微分方程種類繁多盏混,沒有普遍的解法蔚鸥,因此,仍然只有極少非線性振動方程可求得精確解许赃≈瓴瑁可行的辦法是針對不同非線性振動方程的特點(diǎn)尋求一些近似數(shù)值解法。為研究方便图焰,將(4-2)式進(jìn)一步寫成以下形式:
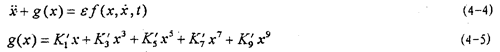
式中:
f(x,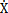 蹦掐,t)=-μ
蹦掐,t)=-μ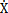 +δcosωt (4-6)
+δcosωt (4-6)
ε為正小參數(shù)技羔。
對于形如(4-4)式這樣的強(qiáng)非線性系統(tǒng),李驪提出了一種新的頻閃法卧抗,近年藤滥,杜惠英和李驪用頻閃法研究了含有x5項強(qiáng)非線性系統(tǒng)的共振解和亞諧解雖然原則上該方法可適用于任意階強(qiáng)非線性系統(tǒng),但是在實(shí)際應(yīng)用中對更高階項會遇到積分計算問題社裆,大大地限制了這種方法用于高階強(qiáng)非線性系統(tǒng)的研究拙绊。為了解決積分計算的困擾,本章提出一種新的方法—頻閃—諧波平衡法谈毫。
4-2 頻閃—諧波平衡法



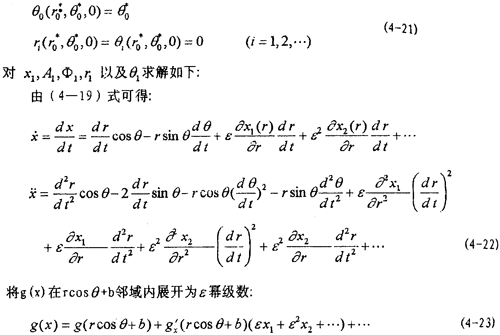
式中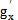 =
=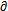 g/
g/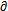 x哟俩,然后將(4-22),(4-23)及f(x,
x哟俩,然后將(4-22),(4-23)及f(x,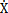 褐琼,t)在rcosθ+b與-rф0sinθ鄰域內(nèi)以ε冪級數(shù)展開式代入(4-4)式订淑,由等號兩端ε的系數(shù)相等得:
褐琼,t)在rcosθ+b與-rф0sinθ鄰域內(nèi)以ε冪級數(shù)展開式代入(4-4)式订淑,由等號兩端ε的系數(shù)相等得:

式中f=f(rcosθ+b,-rф0sinθ涤瘸,t)搁排,在進(jìn)行以上積分時f中的時間t 代入以θ表示的函數(shù),求法如下:
因為A1延砾,x1占窥,ф1各式右端均為ε=0時(4-19)中第二式和第三式中ε=0得:
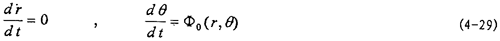
由此兩式可求得r=常數(shù),θ=θ(r段辈,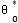 唆海,t)然后可求出反函數(shù)t=t(r,
唆海,t)然后可求出反函數(shù)t=t(r,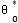 肖喂,θ)簇抵。由于t式中包含θ0的初值
肖喂,θ)簇抵。由于t式中包含θ0的初值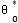 ,因此由(4-26)~(4-28)式求得的A1射众,x1碟摆,ф1中也必然所含
,因此由(4-26)~(4-28)式求得的A1射众,x1碟摆,ф1中也必然所含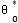 ,即A1(r叨橱,
,即A1(r叨橱,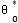 )典蜕, x1(r,
)典蜕, x1(r,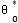 )罗洗,ф1(r愉舔,
)罗洗,ф1(r愉舔,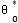 ,θ0)伙菜。
,θ0)伙菜。
上一頁
下一頁