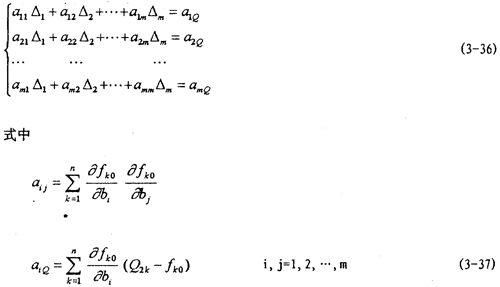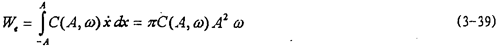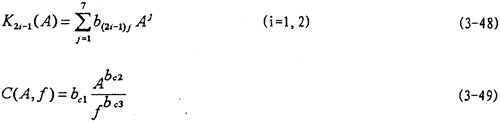當(dāng)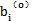
給定時(shí)笋窍，fko和
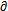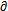fko/bi都是自變量X的函數(shù)，可直接算出趟畏，將（3-31）式代入（3-29）得：
由多元函數(shù)極值存在的必要條件：
得以△i為未知量的一組m個(gè)聯(lián)立方程組
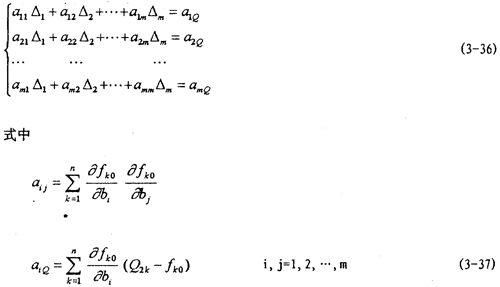
當(dāng)試驗(yàn)數(shù)據(jù)值（Xk甩栈，
2k）泻仙，（k=1，2量没，…玉转，n）和初始近似值bi(0)(i=1,2,...,m)給定后，系數(shù)aij及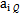
均可算出殴蹄，因此由方程組可解出△i究抓，進(jìn)而得bi的值。當(dāng)算出的|△t |值較大的時(shí)兄哮，可令當(dāng)前的bi值代替原來的初始近似值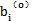肚微，重復(fù)計(jì)算aij气凫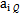，，并解方程組（3-36）得新的△i旭眼，進(jìn)而得bi市协。這種過程可以重復(fù)進(jìn)行，直至|△t |的值小到給定的精度為止料害。
對于非線性參數(shù)辨識問題瞬芒，并在不于迭代工作量有多大，而是在迭代逼近過程中是否收斂掸栋，即迭代過程有可能不按上述方式完成接吠，出現(xiàn)計(jì)算溢出，方程組系數(shù)矩陣病態(tài)等毛不爰尽．出現(xiàn)這些問題的原因大致有三種：一是逼近試驗(yàn)數(shù)據(jù)點(diǎn)（Xk缕圣，2k）的數(shù)學(xué)模型假設(shè)與數(shù)據(jù)點(diǎn)甚遠(yuǎn)，在這種情況下俩莽，必然重新分析系統(tǒng)的內(nèi)在機(jī)理旺坠，建立符合系統(tǒng)特性的新數(shù)學(xué)模型；另一種是初值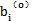選得不好扮超，臺勞級數(shù)展開式完全失真价淌，迭代得到的新bi有可能比原來的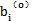更遠(yuǎn)離真解，且越迭代越糟糕瞒津，最后發(fā)散，在這種情況下括尸，迭代是否收斂巷蚪，關(guān)鍵在于初值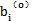的選擇；第三種是參數(shù)辨識的算法不適合或?qū)Τ踔颠x取的要求太高濒翻，在這種情況下屁柏，需選擇更合適的算法或選擇對初值選取要求較低的算法。
按照以上算法有送，編制了計(jì)算機(jī)軟件對（3-14）模型中的參數(shù)進(jìn)行了辨識淌喻，結(jié)果討論如下：
對（3-14）模型，用不同振幅下聯(lián)軸器試驗(yàn)數(shù)據(jù)中代表阻尼力的數(shù)據(jù)來進(jìn)行參數(shù)辨識雀摘，辨識結(jié)果是迭代計(jì)算不收斂宜柱，分析其原因，我們認(rèn)為编喊，一是因?yàn)樾璞孀R的參數(shù)較多拣薄，初始值不易選得與真值較接近，致使迭代不成功潭均；二是此算法可能不適合此模型的參數(shù)辨識校搀。因此三二，有待于尋找能辨識數(shù)學(xué)模型表達(dá)式中參數(shù)的新的有效辨識方法。
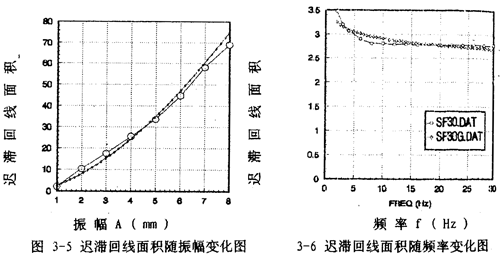
第二種模型是（3-15）式房幌，在這種情況下会刀，用阻尼耗能的能量關(guān)系來辨識阻尼力與振幅等參數(shù)的關(guān)系。由圖3-1可知膜护，聯(lián)軸器每振動一周所消耗的能量掏绍，即遲滯回線的面積S是振幅A的函數(shù)。由數(shù)值積分骇幽，可以算出各振幅變化時(shí)遲滯回線面積瘪决，由此可得遲滯回線面積與振幅的一一對應(yīng)關(guān)系，將這些一一對應(yīng)的數(shù)據(jù)點(diǎn)畫成圖穷娱，如圖3-5中大圓點(diǎn)曲線所示绑蔫，由此分析遲滯回線面積隨振幅變化的規(guī)律，可建立其函數(shù)關(guān)系為：
Sga（A）=asAbs （3-38）
式中as和bs為待辨識參數(shù)泵额。由（3-38）可知配深，面積是參數(shù)bs的非線性函數(shù)，參數(shù)辨識時(shí)用非線性參數(shù)辨識方法嫁盲，高斯-牛頓法篓叶，辨識結(jié)果為as=2.56969，bs=1.62309羞秤，代回（3-38）式并畫出曲線如圖3-5中小點(diǎn)曲線所示缸托。由此可以看出，(3-38）式能較好地描述遲滯回線面積（即聯(lián)軸器阻尼耗能）隨振幅變化的規(guī)律．在用等效粘性阻尼來代替遲滯非線性阻尼的情況下瘾蛋，在具有相同振幅的正弦振動時(shí)俐镐，每周由等效粘性阻尼力耗散的能量為：
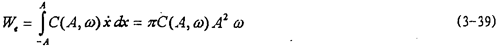
因?yàn)镾ga=We，由（3-38）與（3-39）可得聯(lián)軸器阻尼函數(shù)C（A哺哼，ω）：
將（3-40）式代入（3-15）式得聯(lián)軸器阻尼力模型：
值得注意的是此阻尼力模型的參數(shù)辨識是在研究阻尼耗能過程中佩抹，僅考慮振幅對耗能的影響下得出的，而沒有考慮頻率對耗能的影響虽柜，式中頻率項(xiàng)的出現(xiàn)是由于用等效粘性阻尼代替遲滯非線性阻尼所致飒晴。將（3-41）式畫成曲線得圖3-4中各橢圓，與圖3-2中的閉合曲線相比較可知（3-41）式較好地描述了遲滯非線性阻尼力财偶。將（3-11）拙位、（3-27）和（3-41）式代人（3-8）式即，得聯(lián)軸器恢復(fù)力數(shù)學(xué)模型的函數(shù)表達(dá)式课枉。
2.辨識考慮頻率影響數(shù)學(xué)模型的參數(shù)
考慮頻率影響時(shí)聯(lián)軸器的數(shù)學(xué)模型為（3-17）-（3-22）式碴厂。
a.非線性彈性恢復(fù)力Ql數(shù)學(xué)模型中參數(shù)的辨識
此情況下，1的表達(dá)式為（3-18）-（3-19）式偷被，由于數(shù)學(xué)模型中參數(shù)辨識的復(fù)雜性以及待辨識參數(shù)的非線性性刮盗，在辨識過程中犬耀，先辨識出在不同振幅和頻率下模型中的各參數(shù)α2i-1，β2i-1和γ2i-1书县，然后根據(jù)這些參數(shù)離散散值隨頻率變化的規(guī)律把鹊，建立它們與頻率之間的函數(shù)關(guān)系，再辨識這些函數(shù)關(guān)系式中的各參數(shù)叉屠，從而得到α2i-1 (f)伏尼，β2i-1（f）和γ2i-1 (f）的函數(shù)表達(dá)式，最后得到動剛度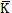
2i-1（A尉尾，f）隨頻率和振幅變化的數(shù)學(xué)模型和彈性恢復(fù)力教學(xué)模型爆阶。
我們用高斯-牛頓法的最小二乘法來辨識，辨識結(jié)果是迭代計(jì)算不收斂沙咏，分析原因認(rèn)為：迭代計(jì)算不收斂辨图，一是初值選擇不合理，二是此算法對初值要求太高肢藐。盡管如此故河，但根據(jù)對聯(lián)軸器非線性彈性恢復(fù)力隨頻率變化的規(guī)律分析，我們?nèi)哉J(rèn)為用（3-18）式來描述聯(lián)軸器彈性恢復(fù)力l=（x,A吆豹，ω）是客觀的和合理的鱼的，式中未知參數(shù)的辨識有待于尋找新的有效的辨識算法。
b.非線性阻尼力2數(shù)學(xué)模型中參數(shù)的辨識
此情況下痘煤，建立的數(shù)學(xué)模型為（3-21）-（3-22）式凑阶。對（3-21）式，辨識所用方法和試驗(yàn)數(shù)據(jù)與辨識（3-14）式相同衷快，所得結(jié)果是迭代計(jì)算不收斂晌砾，究其原因, 認(rèn)為是所用辨識算法不適合此模型的參數(shù)辨識，同時(shí)此算法對初值的要求比較高欠慢。
為了解決以上未決的參數(shù)辨識問題，我們又用了一種算法盲陨，Marquardt算法對（3-14）笋夸、（3-18）和（3-21）模型進(jìn)行了參數(shù)辨識，迭代計(jì)算仍不收斂岂便。為了解決這一問題有待進(jìn)一步尋找有效的辨識算法椿啦。
對于（3-22)模型，我們用阻尼耗能的能量關(guān)系來辨識阻尼力與振幅和頻率的關(guān)系深刁。在前面估董，遲滯回線面積（即阻尼耗能）與振幅的函數(shù)關(guān)系已建立起來，見（3-38）式贪类，而且式中參數(shù)也已辨識出胃愉。同樣射粹，用數(shù)值積分，可以算出振幅一定现粗，頻率變化時(shí)遲滯回線的面積雅镊，由此得出遲滯回線面積與頻率的對應(yīng)關(guān)系，將這些對應(yīng)關(guān)系畫成曲線如圖3-6中大圓點(diǎn)曲線所示刃滓。由遲滯回線面積隨頻率變化的規(guī)律分析仁烹，可建立其函數(shù)關(guān)系為：
Sgf（f）=affbf （3-42）
式中af和bf為待辨識參數(shù)。由此式知咧虎，面積是參數(shù)bf的非線性函數(shù)卓缰，用高斯-牛頓法辨識得af=3.40234,bf=-0.0684433，代回（3-42）式并畫曲線如圖3-6中小點(diǎn)曲線所示砰诵。由此可知征唬，(3-42）式能較好地描述遲滯回線面積隨頻率變化的規(guī)律，阻尼耗散的能量隨頻率的增大而減小胧砰。綜合考慮（3-38）和（3-42）式中阻尼耗散的能量隨振幅和頻率變化的規(guī)律可知鳍鸵，阻尼耗能隨振幅的增大而增大，隨頻率的增大而減小尉间，由此可建立聯(lián)軸器阻尼耗能（即遲滯回線面積）隨振幅A偿乖、頻率f變化的數(shù)學(xué)模型如下：
式中ag,p,q為待定參數(shù)。由此式可知哲嘲，聯(lián)軸器阻尼耗能是振幅和頻率的非線性函數(shù),也是參數(shù)p,q的非線性函數(shù)滨胰。在辨識時(shí)，采用高斯-牛頓法宁斋。根據(jù)（3-38）感栋、(3-42）兩式及其參數(shù)，可知（3-43）中αg參數(shù)的變化域在（2.56969,3.40234）內(nèi)慧男，q值在1.62309附近姥仍，而p值大約在0.068443附近，據(jù)此分析比摆，三個(gè)參數(shù)的初值分別選為：
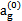=3.0傻牙，q(0)=1.0，p（0)＝0.1
將這三個(gè)初值輸人程序進(jìn)行運(yùn)算休台，一次計(jì)算成功阐泻，三個(gè)參數(shù)值為：
αg=3.382818，q=1.451636征啦，p=0.06649397 (3-44)
將這些參數(shù)代人（3-43）式即得聯(lián)軸器阻尼耗能隨振幅和頻率變化的函數(shù)關(guān)系式担急。
根據(jù)等效原理（3-34）式和Sg=We以及（3-44) 式可得等效粘性阻尼函數(shù)為：
將（3-44）、（3-45）式代入（3-22）式得阻尼力數(shù)學(xué)模型為
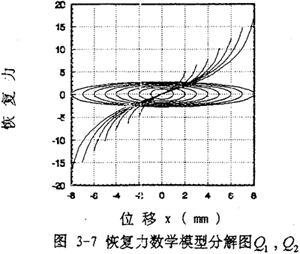
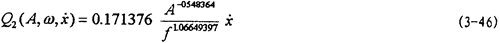
作出（3-46）式的曲線圖如圖3-7中橢圓所示，將圖3-7中橢圓與圖3-4中對應(yīng)橢圓相比較可知蚁趁，式（3-46）能較好地描述非線性遲滯阻尼力裙盾。
3-5 關(guān)于聯(lián)軸器建模與參數(shù)辨識的進(jìn)一步研究
一、數(shù)學(xué)建模與參數(shù)辨識
在對前面關(guān)于聯(lián)軸器建模與參數(shù)辨識工作進(jìn)行思考和對聯(lián)軸器試驗(yàn)結(jié)果進(jìn)行進(jìn)一步深人分析后荣德，提出聯(lián)軸器恢復(fù)力數(shù)學(xué)模型新表達(dá)式：
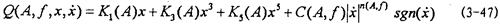
即恢復(fù)力(A,f,x闷煤，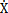
）是振幅A、激勵(lì)頻率f涮瞻、瞬態(tài)位移x和瞬態(tài)速度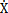的函數(shù)鲤拿，或者說恢復(fù)力Q是剛度函數(shù)K1（A），K3（A）署咽，K5（A）和阻尼函數(shù)C(A,f）以及阻尼成分函數(shù)n(A,f）的函數(shù)近顷，其中阻尼成分函數(shù)n(A,f）描述阻尼的組成情況，n（A,f）=0時(shí)宁否，阻尼為干摩擦阻尼窒升，n(A,f)=1時(shí)，為粘性阻尼慕匠，0＜n（A,f)<1時(shí)饱须，阻尼由粘性阻尼和干摩擦阻尼組成，n（A,f)>1時(shí)隔阔，阻尼成為“高階”阻尼果孝。對于（3-47)式，當(dāng)振幅與頻率一定時(shí)贵式，式中的Kl（A）炼缰，K3（A)，K5（A）和n（A,f）均為定數(shù)衬榕，當(dāng)振幅A和頻率變化時(shí)脸婉，它們均是函數(shù)，因此參數(shù)辨識實(shí)質(zhì)上是參數(shù)函數(shù)的辨識杈夜。首先我們用非線性參數(shù)辨識方法Marquardt法尝赵，根據(jù)試驗(yàn)所得的數(shù)據(jù)，按照（3-47）式對每一遲滯回線進(jìn)行參數(shù)辨識盹组，可以得到對應(yīng)的K1（A)弓呵，K3（A），K5（A),C(A,f)和n（A,f）值疾词，對每種工況下的數(shù)據(jù)隨振幅和頻率變化趨勢進(jìn)行分析后，可以建立剛度函數(shù)灌旧、阻尼函數(shù)和阻尼成份函數(shù)的數(shù)學(xué)表達(dá)式為：
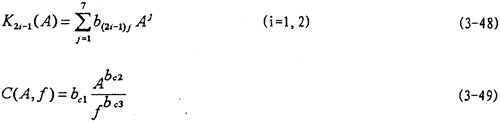
上一頁
下一頁
