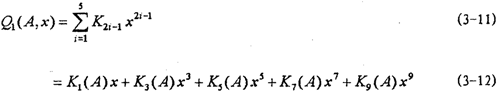第三章 具有非線(xiàn)性遲滯特性鋼絲繩聯(lián)軸器建模與參數(shù)辨識(shí)
3-1 引言
由上章對(duì)聯(lián)軸器振動(dòng)試驗(yàn)研究結(jié)果可知，在大位移振動(dòng)情況下，聯(lián)軸器表現(xiàn)出非線(xiàn)性遲滯特性．這一特性直接與聯(lián)軸器動(dòng)剛度及阻尼有關(guān)，當(dāng)這種聯(lián)軸器用于船舶推進(jìn)軸系時(shí)，將影響到軸系的動(dòng)力特性庵偏，因此弄清楚聯(lián)軸器恢復(fù)力與動(dòng)剛度和阻尼的關(guān)系，即建立聯(lián)軸器恢復(fù)力的數(shù)學(xué)模型是十分重要的，對(duì)于深人分析研究推進(jìn)軸系的動(dòng)力特性也是不可缺少的姨裸。
由鋼絲繩聯(lián)軸器的
-x遲滯回線(xiàn)可知，聯(lián)軸器的遲滯特性不宜用雙線(xiàn)性模型來(lái)描述怨酝，主要原因是雙線(xiàn)性模型與聯(lián)軸器的動(dòng)態(tài)遲滯回線(xiàn)外形相差甚遠(yuǎn)傀缩，雙線(xiàn)性模型將系統(tǒng)剛度系數(shù)處理成二個(gè)線(xiàn)性剛度系數(shù)。這不足以描述鋼絲繩聯(lián)軸器的非線(xiàn)性遲滯特性中的非線(xiàn)性剛度系數(shù)，雙線(xiàn)性模型阻尼僅處理為干摩擦阻尼扑毡，也不足以描述聯(lián)軸器阻尼的復(fù)雜成分胃榕。一階微分方程模型主要用于遲滯系統(tǒng)的隨機(jī)響應(yīng)分析中，這種模型用于計(jì)算遲滯系統(tǒng)的穩(wěn)態(tài)動(dòng)力響應(yīng)很不方便瞄摊，模型中各參數(shù)的物理意義不明確勋又，模型形式不利于各參數(shù)的辨識(shí)，而且彈性力和阻尼力在恢復(fù)力表達(dá)式中不顯現(xiàn)颈缆，不利于理論分析葡料。基于平均和等效原理的跡法和以此為基礎(chǔ)K0等建立的模型都有自己的不足梧货，前者只能描述遲滯恢復(fù)力與位移和速度的關(guān)系佃贞，而不能全面描述遲滯恢復(fù)力與各振動(dòng)參數(shù)的關(guān)系，后者只能描述三個(gè)階次非線(xiàn)性彈簧剛度镐催，其應(yīng)用范圍受到限制隶俄。由此可知，現(xiàn)有描述遲滯特性的數(shù)學(xué)模型都不能用來(lái)描述聯(lián)軸器的非線(xiàn)性遲滯特性椅豆。因此剿蹦，本章將在前人研究的基礎(chǔ)上，研究聯(lián)軸器動(dòng)剛度和阻尼的特性沽叠，建立既能合理描述聯(lián)軸器非線(xiàn)性遲滯特性又能滿(mǎn)足較高精度要求的數(shù)學(xué)模型叹盼。
3-2 擬合分解恢復(fù)力-位移遲滯回線(xiàn)
上一章的試驗(yàn)研究表明，鋼絲繩彈性聯(lián)軸器的本構(gòu)關(guān)系十分復(fù)雜菊榨，其恢復(fù)力是聯(lián)軸器動(dòng)剛度和阻尼的函數(shù)运杭，而動(dòng)剛度和阻尼又是振幅和頻率的函數(shù)。因此函卒，我們將依靠試驗(yàn)獲得的測(cè)量數(shù)據(jù)辆憔，在跡法和文獻(xiàn)的基礎(chǔ)上，深人研究聯(lián)軸器遲滯特性报嵌，建立聯(lián)軸器的數(shù)學(xué)模型躁愿。
由前面聯(lián)軸器位移-恢復(fù)力試驗(yàn)可知，遲滯回線(xiàn)可以分為上沪蓬、下兩條彤钟，分別對(duì)應(yīng)于速度大于零和速度小于零。在鋼絲繩彈性元件性質(zhì)相同和安裝幾何對(duì)稱(chēng)的情況下跷叉，上逸雹、下兩條恢復(fù)力曲線(xiàn)可以認(rèn)為是位移反對(duì)稱(chēng)的。于是可以用冪函數(shù)多項(xiàng)式云挟，按最小二乘法原理來(lái)擬合代表試驗(yàn)數(shù)據(jù)的上梆砸、下兩條恢復(fù)力曲線(xiàn)转质，設(shè)用于擬合上遲滯回線(xiàn)數(shù)據(jù)的冪函數(shù)多項(xiàng)式為：
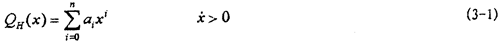
根據(jù)反對(duì)稱(chēng)，用于擬合下遲滯回線(xiàn)數(shù)據(jù)的冪函數(shù)多項(xiàng)式為：
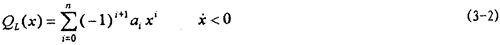
式中版药，H埠限，L分別為聯(lián)軸器遲滯恢復(fù)力上、下曲線(xiàn)茅铺，x為位稱(chēng)旦珊，ai為冪函數(shù)多項(xiàng)式系數(shù)。
冪函數(shù)多項(xiàng)式所取項(xiàng)數(shù)n按擬合的遲滯回線(xiàn)形狀和對(duì)表達(dá)式要求的精度而定毕模。將（3-1）和（3-2）式中冪函數(shù)多項(xiàng)式的奇昵诅、偶次項(xiàng)分開(kāi)寫(xiě)，可進(jìn)一步表示為：
經(jīng)以上數(shù)學(xué)處理腌哎，聯(lián)軸器的動(dòng)態(tài)遲滯回線(xiàn)可以分解成1（x）和2（x貌梦，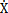
）兩部分，即聯(lián)軸器的遲滯恢復(fù)力由兩部分組成晰淋。式中n取奇數(shù)尸饵。從幾何意義上講，第一部分為一條單值非線(xiàn)性函數(shù)曲線(xiàn)乘儒，第二部分為一條雙值的非線(xiàn)性閉合曲線(xiàn)挠囚。從物理意義上講，第一部分代表遲滯恢復(fù)力中的非遲滯非線(xiàn)性彈性恢復(fù)力脖旱；第二部分代表遲滯恢復(fù)力中的純遲滯非線(xiàn)性阻尼力。
由試驗(yàn)知介蛉，聯(lián)軸器的遲滯恢復(fù)力不僅是位移x和速度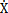的函數(shù)萌庆，而且還是振幅A和頻率ω的函數(shù)，因此遲滯恢復(fù)力的數(shù)學(xué)模型設(shè)為：
（x币旧，
践险，A，ω）=1（x吹菱，A巍虫，ω）+2（x，A鳍刷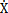，占遥，ω） （3-7）
由此可見(jiàn)，遲滯恢復(fù)力的函數(shù)關(guān)系相當(dāng)復(fù)雜输瓜，
由試驗(yàn)還可以知道瓦胎，頻率增大至一定值后動(dòng)剛度和阻尼僅是振幅A的非線(xiàn)性函數(shù)，在這種情況下尤揣，遲滯恢復(fù)力的數(shù)學(xué)模型可表示為：
（x敛意，她忱，A）=1（x，A）+2（x胶勾，A园秫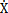，） （3-8）
由此，我們得到兩種形式的聯(lián)軸器恢復(fù)力數(shù)學(xué)模型爹窥，前者為考慮頻率影響的數(shù)學(xué)模型峡稿，后者為不考慮頻率影響的數(shù)學(xué)模型。
至此相吭，盡管我們將遲滯恢復(fù)力擬合分解成了兩部分秧朝，但是l和2取什么樣的函數(shù)形式，仍然是一個(gè)難題郊拄。對(duì)此噩振，分三步來(lái)研究。第一步先求出不同頻率和振幅下遲滯數(shù)據(jù)回線(xiàn)的擬合遲滯回線(xiàn)楚陶，得到對(duì)應(yīng)的各階離散的剛度系數(shù)值钻寿，以及遲滯阻尼耗能值；第二步再找出這些數(shù)值與頻率左刽、振幅的函數(shù)關(guān)系表達(dá)式捺信，從而得到l和2的函數(shù)關(guān)系表達(dá)式，第三步欠痴，通過(guò)參數(shù)辨識(shí)迄靠，尋找出l和2表達(dá)式中的各參數(shù)。
由遲滯回線(xiàn)的形狀可知喇辽，聯(lián)軸器具有強(qiáng)非線(xiàn)性的特性掌挚，為了在數(shù)學(xué)模型中反映出強(qiáng)非線(xiàn)性的特性，選9階冪函數(shù)多項(xiàng)式來(lái)擬合上菩咨、下遲滯回線(xiàn)（n=9)吠式，對(duì)一定頻率和振幅的每一組試驗(yàn)遲滯回線(xiàn)數(shù)據(jù)，由線(xiàn)性最小二乘法原理一辨識(shí)對(duì)應(yīng)的各階擬合系數(shù)抽米。對(duì)圖2-14中各遲滯回線(xiàn)數(shù)據(jù)進(jìn)行擬合特占，將所得的擬合遲滯回線(xiàn)與圖2-14的遲滯回線(xiàn)畫(huà)在一起，如圖3-1（a）所示云茸，由此圖可知是目，兩者重合性很好。
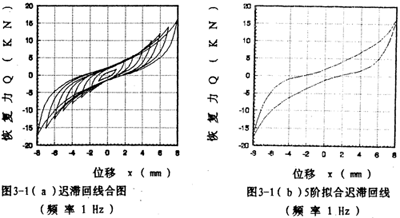
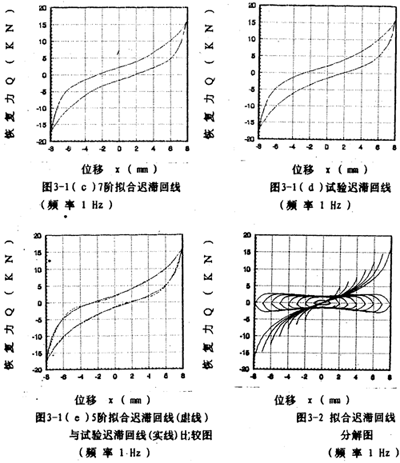
為了說(shuō)明5階和7階冪函數(shù)多項(xiàng)式擬合的精度情況么鹊，以振幅A=8毫米荚谢，頻率為1赫茲為例，畫(huà)出擬合回線(xiàn)分別如圖3-1（b）呐品、3-1（c）所示凯挟，將它們與對(duì)應(yīng)試驗(yàn)回線(xiàn)圖3-1（d）比較逸铆，可知7階擬合精度高于5階。圖3-1（e）為圖3-1（b）與圖3-1（d）的合圖辱滤。
為了得到（3-6）式所示的l苦钱，2，將擬合得到的各冪函數(shù)多項(xiàng)式奇沽贸、偶次項(xiàng)分開(kāi)寫(xiě)成（3-5）式形式并作對(duì)應(yīng)的曲線(xiàn)圖避晾，如圖3-2（見(jiàn)34頁(yè)）所示，這樣就將恢復(fù)力分解成了單值非線(xiàn)性函數(shù)曲線(xiàn)和雙值的非線(xiàn)性函數(shù)閉合曲線(xiàn)抑昨，由此得到了對(duì)應(yīng)的l（x）和2（x啥匀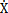，）的若干組函數(shù)表達(dá)式：
式（3-9）中各系數(shù)a2i-1實(shí)質(zhì)上代表聯(lián)軸器彈性恢復(fù)力在對(duì)應(yīng)頻率、振幅下的各階剛度系數(shù)赚铅。
3-3 聯(lián)軸器數(shù)學(xué)建模
一催首、不考慮頻率影響的數(shù)學(xué)模型
由于聯(lián)軸器恢復(fù)力僅在一個(gè)小范圍內(nèi)受頻率的影響，當(dāng)頻率達(dá)到一定值后泄鹏，聯(lián)軸器恢復(fù)力僅是振幅的函數(shù)郎任，在這種情況下，數(shù)學(xué)模型的表達(dá)式為（3-8）式备籽。下面分別研究l和2函數(shù)表達(dá)式的結(jié)構(gòu)形式舶治。
1.非遲滯非線(xiàn)性彈性恢復(fù)力l的數(shù)學(xué)模型
在不考慮頻率影響的情況下，聯(lián)軸器彈性恢復(fù)力车猬，由以上分析霉猛，可以建立其數(shù)學(xué)模型如下：
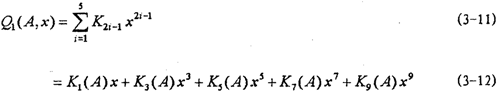
式中K1（A）--K9（A）是鋼絲繩聯(lián)軸器第一～九階彈簧剛度函數(shù)。
這樣的數(shù)學(xué)模型充分地考慮了高階非線(xiàn)性彈性力的影響珠闰。式中K2i-1（A）僅是振幅的函數(shù)惜浅，其數(shù)學(xué)模型為：
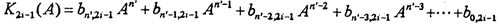（i=1，2铸磅，3，4杭朱，5） （3-13）
式中n′根據(jù)精度要求而定阅仔。
2.遲滯非線(xiàn)性阻尼力2的數(shù)學(xué)模型
由擬合遲滯回線(xiàn)分解圖3-2中各閉合曲線(xiàn)知，聯(lián)軸器中的阻尼成分非常復(fù)雜窑笑，有可能是多種阻尼的組合秕射，根據(jù)聯(lián)軸器彈性元件變形及工作情況，可以認(rèn)為聯(lián)軸器阻尼含有粘性阻尼和干摩擦阻尼的成份較多综界，因此瞎角，在這種情況下我們建立以下二種阻尼力模型：
(1）復(fù)合型阻尼力模型
2=a[a0+a2x2+a4x4+a6x6]sgn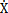（）+C|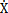|nsgn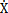（） （3-14）
式中第一項(xiàng)代表除粘性阻尼力和干摩擦力以外的其它阻尼力成份，系數(shù)α決定這些阻尼力所占比例贴祷，故定義為阻尼比例控制系數(shù)覆靖；第二項(xiàng)代表粘性阻尼力和干摩擦阻尼力綜合阻尼力成份攒筛，當(dāng)n=o時(shí)，這項(xiàng)為Csgn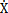（）午禽，代表干摩擦阻尼力鸳辈，當(dāng)n=1時(shí)，這項(xiàng)為C|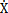|sgn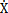（）绿锋，代表粘性阻尼力崩旱，當(dāng)n在（0，1）區(qū)間變化時(shí)澄港，第二項(xiàng)代表的是粘性阻尼力和干摩擦阻尼力的混合阻尼力椒涯，系數(shù)n決定兩種阻尼各占份額多少，定義為粘摩阻尼分配系數(shù)回梧。式中a0,a2废岂，a4，a6漂辐，C,n和α均是振幅的函數(shù)泪喊。
(2）等效粘性阻尼力模型
用等效粘性阻尼來(lái)描述遲滯非線(xiàn)性阻尼，其恢復(fù)力構(gòu)建為：
2=C（A髓涯，ω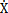） （3-15）
由于聯(lián)軸器阻尼成份的復(fù)雜性袒啼，以上建立的二種阻尼恢復(fù)力模型中哪一種用來(lái)描述聯(lián)軸器阻尼力更為合理，有待于參數(shù)辨識(shí)后才能確定纬纪。對(duì)于模型（3-14)蚓再，我們將先辨識(shí)出在不同振幅下模型中的各個(gè)參數(shù)，然后再找出這些參數(shù)與振幅的函數(shù)關(guān)系包各。對(duì)于模型（3-15)摘仅，我們將根據(jù)一個(gè)振動(dòng)周期內(nèi)遲滯非線(xiàn)性阻尼所耗散的能量與等效粘性阻尼所消耗的能量相等的能量關(guān)系找出等效粘性阻尼函數(shù)C(A，ω）與振幅和頻率的關(guān)系问畅。
上一頁(yè)
下一頁(yè)
