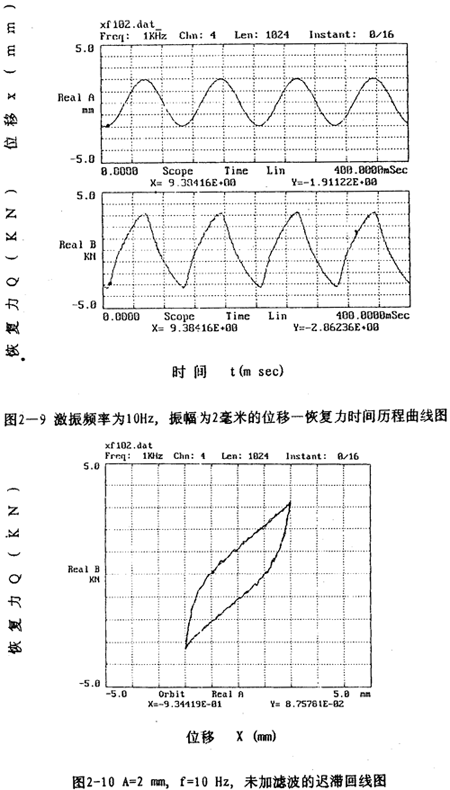
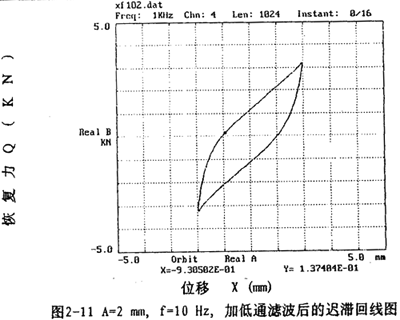
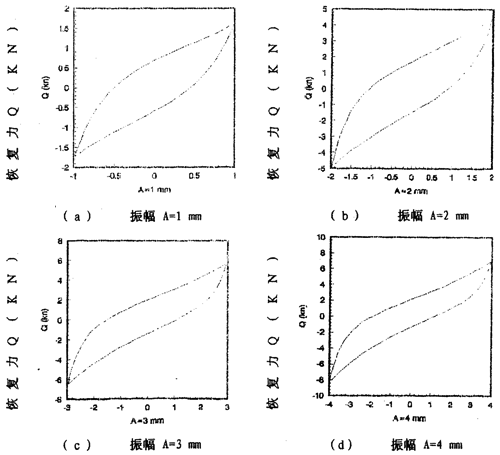
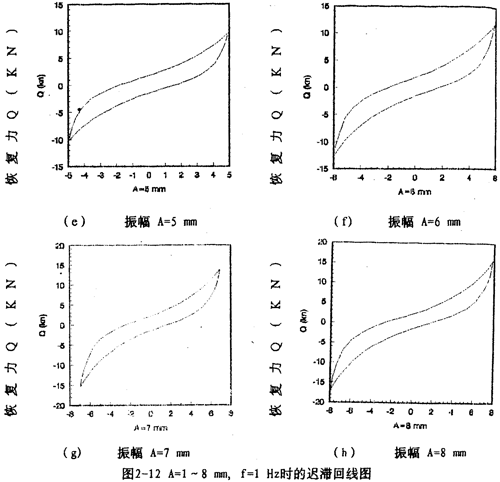
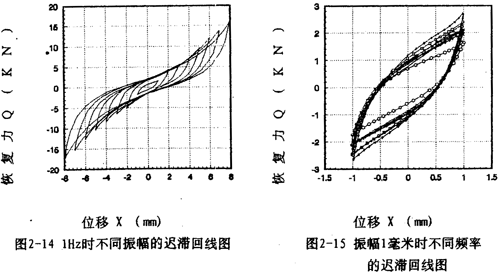
圖2-9(見26頁(yè))表示激振頻率為1OHz枪素,振動(dòng)位移幅值為±2毫米的位移和恢復(fù)力時(shí)間歷程圖墩剖,圖2-10(見26頁(yè))杖们、圖2-11(見27頁(yè))為對(duì)應(yīng)的遲滯回線圖揽思。圖2-l2(見27袜腥、28頁(yè))表示激振頻率為IHz,振動(dòng)位移幅值分別為±(1-8)毫米的位移一恢復(fù)力圖钉汗,圖2-14(見29頁(yè))則為圖2-12的合圖羹令,由圖2-14同頻率不同振幅的八條遲滯回線分析可知,大撓度剛絲繩彈性聯(lián)軸器的動(dòng)剛度與振動(dòng)幅值有關(guān)损痰,同時(shí)福侈,從遲滯回線面積(表示聯(lián)軸器阻尼所耗散的能量)可知聯(lián)軸器的阻尼與振動(dòng)幅值也有關(guān),即聯(lián)軸器的動(dòng)剛度和阻尼均是振幅的非線性函數(shù)卢未。
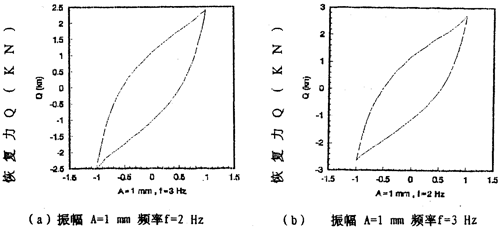
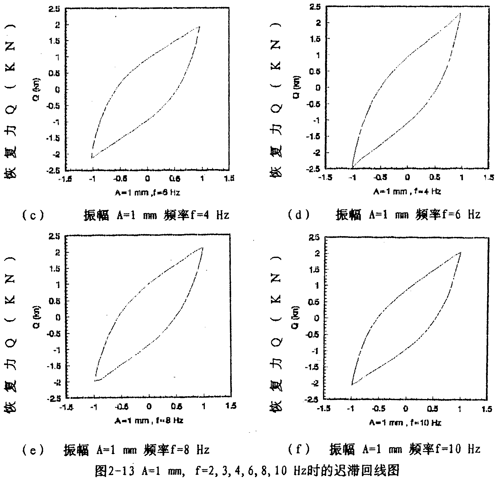
圖2-13(見28肪凛、29頁(yè))表示振幅為l毫米,激振頻率分別為2,3,4,6,8,10Hz的遲滯回線圖躏宗,圖2-15(見29頁(yè))表示振幅為1毫米邦霸,激振頻率為1,2,3,4,6,8,10,20,30Hz的遲滯回線合圖。由圖2-15可知根爆,彈性聯(lián)軸器的動(dòng)剛度與振動(dòng)頻率有關(guān)幕封,即隨著頻率增大,對(duì)應(yīng)的遲滯回線的恢復(fù)力與位移的比值變小瓦腋,當(dāng)頻率在8Hz至30Hz范圍內(nèi)時(shí)窒兼,遲滯回線基本重合,由此可知鋼絲繩聯(lián)軸器動(dòng)剛度在一定頻率范圍內(nèi)與頻率有關(guān)妙旅、當(dāng)頻率增大到8Hz以后军裂,聯(lián)軸器的動(dòng)剛度不再隨頻率變化而變化,因而聯(lián)軸器的動(dòng)剛度在一定頻率范圍內(nèi)與頻率有關(guān)战覆,當(dāng)頻率增大到8Hz以后威沙,聯(lián)軸器的動(dòng)剛度不再隨頻率變化而變化,因而聯(lián)軸器的動(dòng)剛度在一定頻率范圍內(nèi)是頻率的非線性函數(shù)柬乓,當(dāng)頻率增大到一定值后攘活,動(dòng)剛度與頻率無(wú)關(guān),同樣玄呛,聯(lián)軸器的阻尼在一定頻率范圍內(nèi)的頻率的非線性函數(shù)阅懦,當(dāng)頻率增大到一定值后(這里是8Hz),阻尼與頻率無(wú)關(guān)徘铝。
2-5 小結(jié)
通過對(duì)鋼絲繩彈性聯(lián)軸器的振動(dòng)試驗(yàn)耳胎、信號(hào)處理和分析,可以得到以下結(jié)論:
1.開發(fā)MTS材料試驗(yàn)機(jī)對(duì)大撓度彈性聯(lián)軸器進(jìn)行大位移振動(dòng)試驗(yàn)是可行的惕它,解決了激振器或振動(dòng)臺(tái)不能同時(shí)滿足大位移怕午、頻率和激振力達(dá)到一定要求的難題废登,為大位移振動(dòng)試驗(yàn)開辟了新的途徑。
2.鋼絲繩彈性聯(lián)軸器能產(chǎn)生動(dòng)態(tài)大位移郁惜,具有補(bǔ)償主機(jī)在運(yùn)行中出現(xiàn)大位移的能力堡距。聯(lián)軸器及鋼絲繩彈性元件能在設(shè)計(jì)范圍內(nèi)正常工作,但有的彈性元件出現(xiàn)鋼絲斷絲現(xiàn)象兆蕉,夾持板在低頻大位移振動(dòng)時(shí)變形較大羽戒,因此有必要對(duì)彈性元件的聯(lián)接方式進(jìn)行改進(jìn)。
3.鋼絲繩彈性聯(lián)軸器的恢復(fù)力具有非線性遲滯特性虎韵,在大位移振動(dòng)情況下表現(xiàn)出動(dòng)剛度非線性和阻尼非線性的特性综俄,聯(lián)軸器的動(dòng)剛度是振動(dòng)幅值和頻率的非線性函數(shù),但當(dāng)頻率增大到一定值后仲寇,動(dòng)剛度僅為振幅的非線性函數(shù)制沦。同樣,聯(lián)軸器的阻尼在一定頻率范圍內(nèi)是振幅和頻率的非線性函數(shù)购具,但當(dāng)頻率增大至一定值后榛青,阻尼僅是振幅的非線性函數(shù)。因此大撓度彈性聯(lián)軸器的本構(gòu)關(guān)系是一非線性泛函惯醇。
4.以上研究成果為聯(lián)軸器恢復(fù)力數(shù)學(xué)模型的建立曙惋、參數(shù)辨識(shí)提供了依據(jù)和準(zhǔn)備了數(shù)據(jù)。
上一頁(yè)
下一頁(yè)







