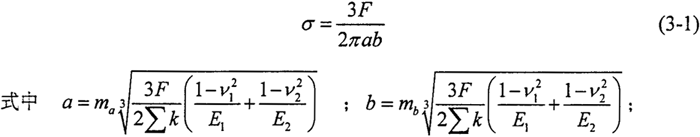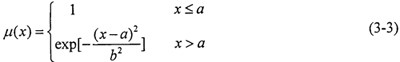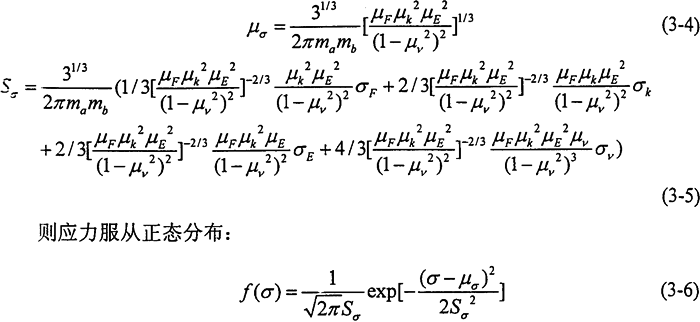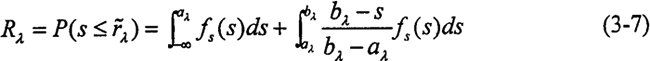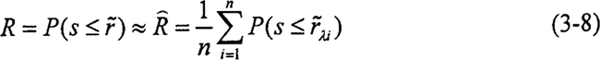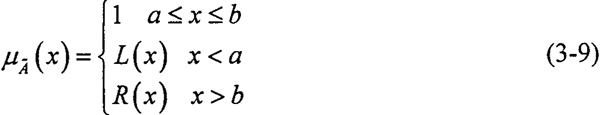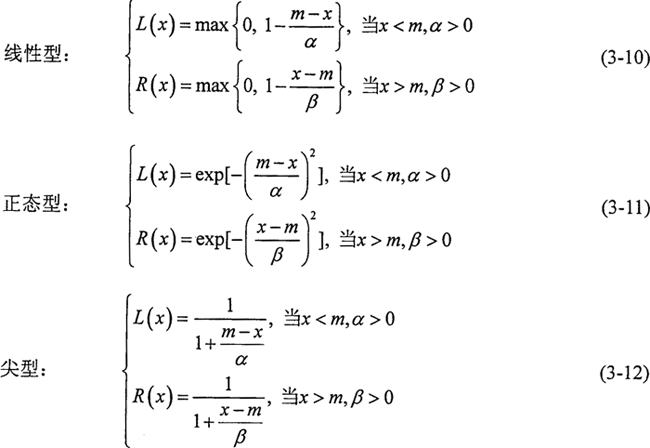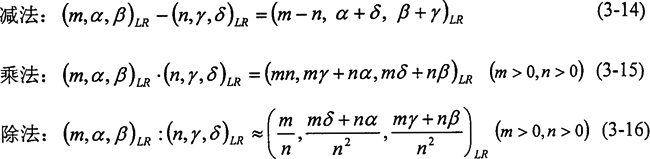第3章 圓柱正弦活齒減速器模糊可靠性的研究
3.1引言
圓柱正弦活齒減速器可以應(yīng)用在航天機(jī)械、采油裝置及機(jī)器人傳動(dòng)等復(fù)雜的工作環(huán)境中饲悟，其可靠性的好壞直接影響生產(chǎn)的效率和安全咏编，為此，對(duì)它進(jìn)行可靠性研究具有十分重要的意義熄朴。圓柱正弦活齒減速器的可靠性研究應(yīng)包括以下兩個(gè)方面：一方面是機(jī)械零部件本身的可靠度研究，即組成減速器系統(tǒng)的各個(gè)零部件完成所需功能的能力。另一方面是減速器樂(lè)統(tǒng)的可靠性研究雾鸠。其中系統(tǒng)的可靠度還取決于系統(tǒng)中機(jī)械零部件組合的方式限牢。
在圓柱正弦活齒減速器系統(tǒng)中，活齒與正弦滾道齒面的接觸方式為點(diǎn)接觸纪娄，則正弦滾道齒面與活齒的工作表面發(fā)生點(diǎn)蝕或膠合是該嚙合副的主要失效形式戈裳，對(duì)其進(jìn)行接觸強(qiáng)度的可靠性研究，對(duì)提高齒面強(qiáng)度启毁、降低失效概率具有非常重要的意義橘蹭。接觸強(qiáng)度的點(diǎn)蝕破壞是由于損傷積累引起性能下降最終導(dǎo)致故障的出現(xiàn)，系統(tǒng)從完好到失效是一個(gè)循序漸進(jìn)的過(guò)程页衙，其間呈現(xiàn)出亦此亦彼的模糊狀態(tài)摊滔，因此在機(jī)械系統(tǒng)中隨機(jī)性與模糊性是密切相關(guān)的，本章將模糊數(shù)學(xué)方法和隨機(jī)方法結(jié)合起來(lái)店乐，對(duì)圓柱正弦活齒傳動(dòng)的接觸強(qiáng)度進(jìn)行模糊可靠性分析艰躺，突破了常規(guī)設(shè)計(jì)方法中將應(yīng)力、強(qiáng)度視為確定量而忽視其隨機(jī)性和模糊性的局限性眨八，使設(shè)計(jì)結(jié)果更加合理腺兴，更為真實(shí)。
在系統(tǒng)可靠性研究方法中廉侧，故障樹(shù)分析（FTA）是一種用于復(fù)雜系統(tǒng)可靠性和安全性分析的有效方法页响，F(xiàn)TA是一種圖形演繹方法，能通過(guò)對(duì)可能造成系統(tǒng)故障的多種因素（包括軟件段誊、硬件闰蚕、環(huán)境、人為因素）進(jìn)行分析枕扫，畫(huà)出邏輯框圖即故障樹(shù)陪腌，從而確定系統(tǒng)故障原因的各種可能組合方式或其發(fā)生概率。本章在分析圓柱正弦活齒減速器系統(tǒng)結(jié)構(gòu)及功能關(guān)系的基礎(chǔ)上燥颠，建立圓柱正弦活齒減速器的故障樹(shù)叼稍，確定了系統(tǒng)的最小割集。將模糊數(shù)學(xué)引入傳統(tǒng)的故障樹(shù)分析中睛赁，根據(jù)建立的故障樹(shù)中各事件的邏輯關(guān)系闻荠，采用模糊數(shù)的運(yùn)算法則及模糊算子AND和OR計(jì)算出系統(tǒng)以“輸出軸不傳遞扭矩”為故障的模糊概率值。
為體現(xiàn)真實(shí)工況下減速器系統(tǒng)的可靠性情況徙祥，在建立故障樹(shù)的基礎(chǔ)上藻拟，基于Monte-Carlo方法對(duì)圓柱正弦活齒減速器進(jìn)行可靠性的數(shù)字仿真。由此得到了系統(tǒng)故障的可靠度廉贤、失效概率及壽命分布等一系列可靠性指標(biāo)卑聚，并通過(guò)對(duì)基本部件模式重要度的分析遥妒，找出系統(tǒng)薄弱環(huán)節(jié)，對(duì)改進(jìn)和重新設(shè)計(jì)系統(tǒng)具有很大約啟發(fā)性和指導(dǎo)性纽秽。
3.2圓柱正弦活齒傳動(dòng)副的接觸強(qiáng)度模糊可靠性研究
在機(jī)械傳動(dòng)系統(tǒng)中珍询，由于受到彈性模量、幾何尺寸掰腌、載荷分配等因素的影響策橘，各零件的工作應(yīng)力均具有隨機(jī)性，對(duì)此可用統(tǒng)計(jì)的方法將其視為隨機(jī)變量來(lái)處理娜亿；另一方面丽已，由于受到各種客觀條件的限制，傳動(dòng)零件的接觸強(qiáng)度等設(shè)計(jì)變量難以精確定量买决，存在亦此亦彼的狀態(tài)沛婴，將這種變量處理為模糊變量，用模糊集合與隸屬函數(shù)來(lái)描述策州∪澄叮考慮到應(yīng)力和強(qiáng)度作為隨機(jī)變量和模糊變量，因此機(jī)誡傳動(dòng)系統(tǒng)的強(qiáng)度設(shè)計(jì)可按模糊可靠性設(shè)計(jì)方法進(jìn)行墓它突破了常規(guī)設(shè)計(jì)方法中將應(yīng)力够挂、強(qiáng)度視為確定量而忽視其隨機(jī)性和模糊性的局限性旁仿，使設(shè)計(jì)結(jié)果更加趨于合理，因此更為接近實(shí)際情況孽糖。
3.2.l接觸應(yīng)力計(jì)算
圓柱正弦活齒傳動(dòng)的嚙合副在載荷作用下枯冈，活齒分別與主動(dòng)軸的外滾道及殼體的內(nèi)滾道接觸，一般滾道半徑取r′= (1.04-1.11)r,r為活齒半徑办悟〕咀啵活齒與滾道的接觸問(wèn)題，可看作兩自由曲面體的彈性接觸問(wèn)題鸦呆，根據(jù)赫茲（Hertz）應(yīng)力理淪瓣挂，在外加總載荷F作用下兩自由曲面彈性體的接觸應(yīng)力計(jì)算公式為
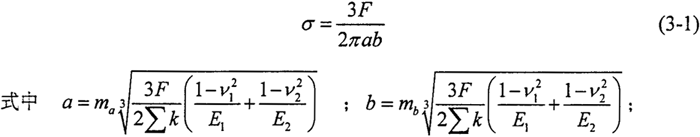
ma、mb——與橢圓偏心率有關(guān)的系數(shù)畔香，可根據(jù)∑k及F（k）查表得到类埋；
F（k）——主曲率函數(shù)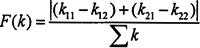
；
∑k——主曲率和∑k=k11+k12+k21+k22猪褐，（1/mm）鼓辈；
k11、k12——活齒齒面的兩個(gè)主曲率（1/mm）和蛀；
k21失跷、k22——正弦滾道齒面的兩個(gè)主曲率（l/mm）。
由于嚙合副兩接觸面的材料相同搂棱，故選取彈性模量E1=E2=E叔梆，泊松比v1=v2=v沫流。通過(guò)對(duì)圓柱正弦活齒傳動(dòng)進(jìn)行受力分析可知，在正弦滾道的拐點(diǎn)附近臂外，活齒與滾道間的接觸力及接觸應(yīng)力均達(dá)到最大值窟扑，因此活齒與正弦滾道齒面的最大接觸應(yīng)力公式可寫(xiě)為
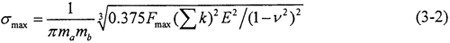
3.2.2接觸強(qiáng)度的模糊可靠性研究
滾道齒面從完好狀態(tài)到失效狀態(tài)，其許用應(yīng)力[σH]是一個(gè)漸進(jìn)的衰減過(guò)程漏健，為了更真實(shí)的反映[σH]的模糊性，本文采用降半正態(tài)分布的隸屬函數(shù)來(lái)表示[σH]橘霎。降半正態(tài)分布的隸屬函數(shù)為
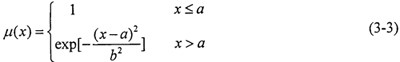
式中 u（x)- [σH]的隸屬度蔫浆；a、b為分布系數(shù)姐叁。
隸屬函數(shù)曲線如圖3-1瓦盛。
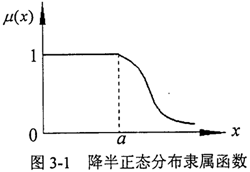
將F、∑k視為隨機(jī)變量外潜，并近似按“3σ”法求出其均值μF原环、μk與標(biāo)準(zhǔn)差SF、Sk处窥，根據(jù)文獻(xiàn)嘱吗，彈性模量E、泊松比v均為隨機(jī)變量滔驾，且近似服從正態(tài)分布谒麦，彈性模量的變異系數(shù)對(duì)鋼而言不超過(guò)0.03，即彈性模量的標(biāo)準(zhǔn)差為6180MMPa采冕，而泊松比的變異系數(shù)一般在2%-3%左右援愁，則泊松比的標(biāo)準(zhǔn)差為0.009。按可靠度計(jì)算的一次二階矩原理孩青，將齒面接觸應(yīng)力的表達(dá)式在基本變量的平均值點(diǎn)處展開(kāi)成泰勒級(jí)數(shù)径揭，僅取級(jí)數(shù)的線性項(xiàng)，則可近似求得應(yīng)力的均值μa與標(biāo)準(zhǔn)差Sσ分別為：
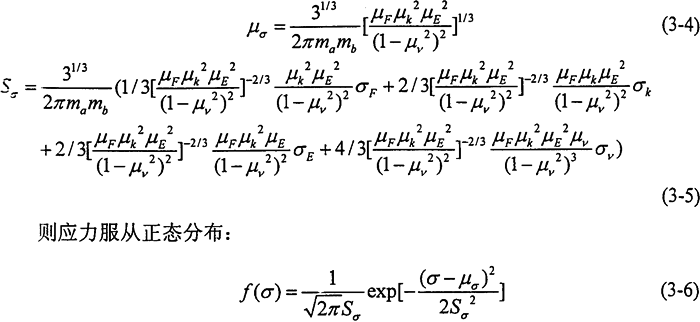
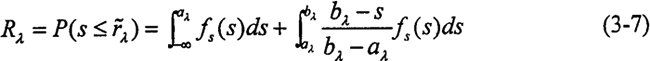
應(yīng)用數(shù)字仿真法求出零件的可靠度R森肉，即在（O,1）內(nèi)產(chǎn)生均勻分布的隨機(jī)數(shù)作為閾值λ1雌夕，并利用式（3-7）計(jì)算此時(shí)零件的可靠度Rλi，在仿真次數(shù)n足夠大時(shí)脾仁，零件的可靠度可表示為：
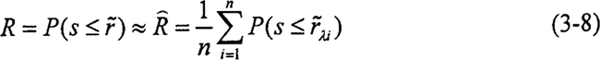
3.2.3圓柱正弦活齒傳動(dòng)接觸強(qiáng)度的可靠性計(jì)算
圓柱正弦活齒減速器的結(jié)構(gòu)和性能參數(shù)為Z1=1辈殃、Z3=4、A=4mm秕栓、r=4mm债案、輸出軸扭矩T=20N.m，其主要零件如活齒邢入、主動(dòng)軸截型、導(dǎo)架及殼體的材料選用GCr15趴荸，淬火后硬度為HRC=58～62，由于圓柱正弦活齒傳動(dòng)采用二硫化鋁作為固體潤(rùn)滑劑宦焦，考慮到二硫化鑰的最大抗壓強(qiáng)度為2800MPa发钝，根據(jù)模糊數(shù)學(xué)中確定容差的擴(kuò)增系數(shù)法，該傳動(dòng)的主要零件的許用接觸應(yīng)力選為2450～2800MPa波闹。將上述參數(shù)代入式（3-4）酝豪、（3-5）中，求得主動(dòng)軸正弦滾道與殼體正弦滾道接觸應(yīng)力的均值和方差精堕，再利用式（3-8)孵淘，仿真次數(shù)n選取2000次，計(jì)算圓柱正弦活齒傳動(dòng)正弦滾道的接觸強(qiáng)度的可靠度見(jiàn)表3-1歹篓。
表3-1滾道接觸強(qiáng)度的可靠度
| |
均值（MPa） |
方差（MPa） |
可靠度 |
| 主動(dòng)軸 |
2322.9 |
192.12 |
0.9744 |
| 殼體 |
2325.7 |
172.31 |
0.9781 |
| 導(dǎo)架 |
2284.4 |
300.51 |
0.9145 |
由表3-1可知瘫证，導(dǎo)架的接觸強(qiáng)度可靠度最低，是整個(gè)系統(tǒng)可靠性的薄弱環(huán)節(jié)庄撮。因此背捌，在結(jié)構(gòu)設(shè)計(jì)中，應(yīng)盡量提高導(dǎo)架的接觸強(qiáng)度可靠度湘乐，以改善圓柱正弦活齒減速器系統(tǒng)的可靠性蝌飘。
3.3減速器系統(tǒng)的模糊可靠性研究
故障樹(shù)分析是分析系統(tǒng)可靠性的一種方法，它根據(jù)系統(tǒng)的結(jié)構(gòu)或功能關(guān)系钩裆，利用圖形演繹的方法把故障傳遞的邏輯關(guān)系表達(dá)出來(lái)舞懦，對(duì)此可逐級(jí)分析系統(tǒng)故障發(fā)生的原因，對(duì)系統(tǒng)進(jìn)行故障概率的計(jì)算图盖，以便采取相應(yīng)的措施毕蕉，來(lái)提高系統(tǒng)的可靠性。
3.3.1減速器系統(tǒng)故障樹(shù)的建立
根據(jù)圓柱正弦活齒減速器的結(jié)構(gòu)及其實(shí)現(xiàn)的功能企著，采用自上而下的方法建立故障樹(shù)乙笛，首先選取“輸出軸不能傳遞扭矩”作為頂事件，然后找出導(dǎo)致頂事件的所有可能直接原因冒溜，作為第一級(jí)中間事件刽室，用相應(yīng)的事件符號(hào)將其表達(dá)出來(lái)，并用適合的邏輯門(mén)符號(hào)表示中間事件與頂事件之間的邏輯關(guān)系饶辆。依此類推酪律，逐級(jí)向下發(fā)展，直到找出引起系統(tǒng)故障的全部原因翻默，作為底事件缸沃，由此建立了圓柱正弦活齒減速器的故障樹(shù)（圖3-2）。
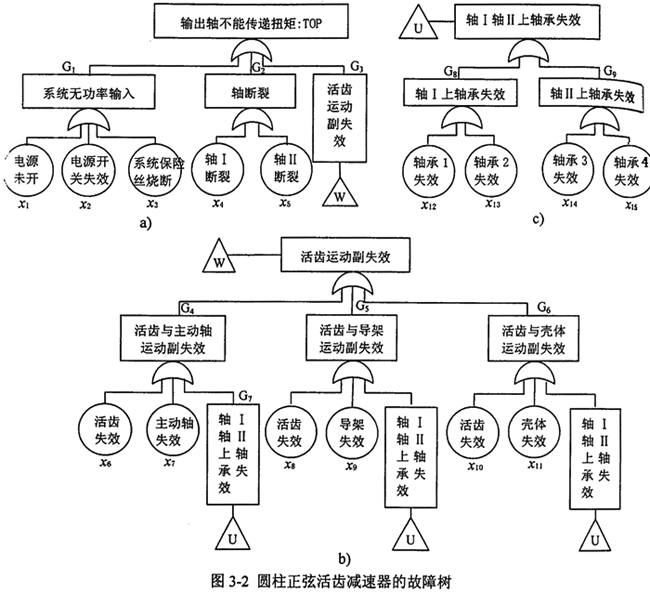
3.3.2減速器系統(tǒng)故障樹(shù)的分析
故障樹(shù)的分析包括定性分析和定量分析修械。定性分析的主要任務(wù)是尋找故障樹(shù)的全部最小割集和最小路集趾牧，一個(gè)最小割集代表系統(tǒng)的一種失效模式检盼，一個(gè)最小路集代表系統(tǒng)一種正常模式。通過(guò)對(duì)最小割集和最小路集的研究翘单，可以發(fā)現(xiàn)系統(tǒng)的薄弱環(huán)節(jié)和最關(guān)鍵的部分吨枉，以便針對(duì)具體對(duì)象采取相應(yīng)的措施，有利于維持和提高系統(tǒng)的功能哄芜。本本文只討論系統(tǒng)的失效模式貌亭，故須尋找出故障樹(shù)的最小割集即可。根據(jù)對(duì)圓柱正弦活齒減速器的故障樹(shù)分析得出最小割集為{xi}忠烛，i=1属提，2…，15美尸。他們分別對(duì)應(yīng)系統(tǒng)15種失效模式。
故障樹(shù)的定量分析是運(yùn)用故障樹(shù)中建立的邏輯關(guān)系僵馒，根據(jù)底事件發(fā)生的概率推導(dǎo)出頂事件發(fā)生的概率幼氏，從而對(duì)系統(tǒng)的可靠性、安全性作出評(píng)價(jià)绸秸。故障樹(shù)中各種事件間的因果關(guān)系用各種“門(mén)”來(lái)描述嬉拾，并且大多可以等效為邏輯“與門(mén)”和“或門(mén)”。根據(jù)“與門(mén)”和“或門(mén)”所表示的事件關(guān)系匠似，并假設(shè)各個(gè)事件互相獨(dú)立臊吓，根據(jù)表3-2即可計(jì)算活齒減速器中各中間事件和頂事件的發(fā)生概率。
表中 P（T）——頂事件發(fā)生概率暗沉；
P（xi）——底事件發(fā)生概率英谢，i=1，2里淡，…刃伞，15；
P（Gi）——中間事件發(fā)生概率谎跨。i=1钥嫌，2，…男杈，9丈屹。
3.3.3圓柱正弦活齒減速器的模糊故障樹(shù)分析
故障樹(shù)分析重要的環(huán)節(jié)是獲得事件發(fā)生的概率。傳統(tǒng)的故障樹(shù)分析以布爾代數(shù)為基礎(chǔ)伶棒，把事件發(fā)生的概率處理成精確值旺垒，然而由于實(shí)際工作環(huán)境的模糊性及數(shù)據(jù)的不精確，會(huì)對(duì)確定事件的概率產(chǎn)生影響苞冯，因此難以用一精確值來(lái)表示事件發(fā)生的概率袖牙。在傳統(tǒng)故障樹(shù)分析中侧巨，當(dāng)事件發(fā)生的概率難以精確賦值時(shí)，可對(duì)故障樹(shù)進(jìn)行模糊分析鞭达。
3.3.3.1模糊分析的理論基礎(chǔ) 在故障樹(shù)的模糊分析中司忱，采用模糊數(shù)來(lái)描述事件發(fā)蘭的概率。模糊數(shù)是由概念上的模糊性或各種模糊因素的影響而造成定量處理時(shí)的不確定性畴蹭。以模糊數(shù)描述概率值坦仍，帶有人的主觀性，強(qiáng)調(diào)了人在系統(tǒng)可靠性分析與評(píng)價(jià)中的重要性叨襟。因此堆嘿，故障樹(shù)的模糊分析不僅可減少獲取事件發(fā)生概率精確值的難度，而且能結(jié)合工程中的實(shí)際經(jīng)驗(yàn)和判斷構(gòu)造模糊數(shù)為隸屬函數(shù)慌缨，較準(zhǔn)確地把它們描述出來(lái)氏走，并在一定程度上允許存在描述誤差，具有較大的靈活性和適應(yīng)性娱背。
定義1 模糊數(shù)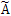
為實(shí)數(shù)域R上的正規(guī)凸模糊集讥燎，其隸屬函數(shù)滿足
（1）maxμ（x）=1 x∈R
（2）μ（x）是逐段連續(xù)的
定義2 若模糊數(shù)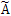的隸屬函數(shù)滿足
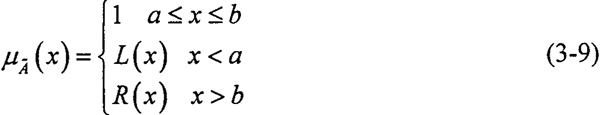
則稱模糊數(shù)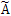為L(zhǎng)-R型模糊數(shù)，L(x）烂秘、R(x）稱為模糊數(shù)的左掰魁、右參照函數(shù)。工程中裳雕，模糊數(shù)隸屬度為1的數(shù)通常只有一點(diǎn)低流，因此模糊數(shù)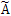可表示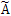=（m，a帜浇，β）辨蓄。其中m是模糊數(shù)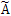的均值，對(duì)應(yīng)隸屬度為l的數(shù)囤恶；a偿荷、β分別為左、右分布唠椭；當(dāng)a跳纳、β為零時(shí)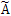，不是模糊數(shù)贪嫂。分布a寺庄、β越大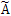，越模糊力崇。
常用的L-R參照函數(shù)為：
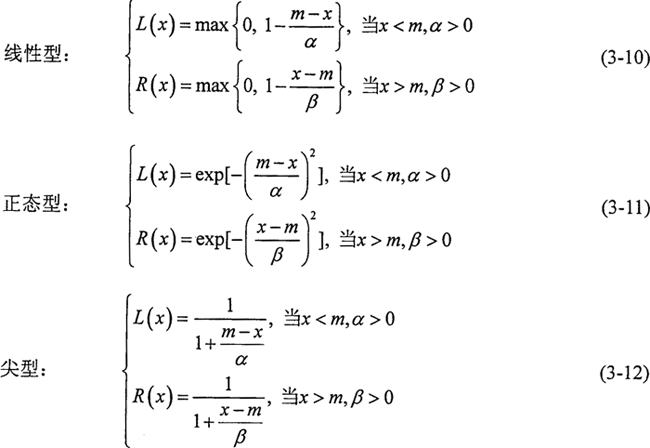
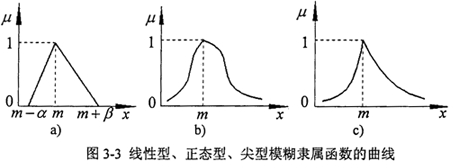
線性型參照函數(shù)在“完全屬于”和“完全不屬于”之間的中介狀態(tài)是線性變化的（圖3-3a）斗塘，當(dāng)x≤m-α和x≥m+β時(shí)，μ=0，說(shuō)明在（m-α馍盟，m+β）區(qū)間之外的數(shù)值完全不屬于該模數(shù)數(shù)于置。而其他兩種類型的隸屬函數(shù)曲線兩端延伸至無(wú)窮遠(yuǎn)（圖3-3b，c）說(shuō)明整個(gè)數(shù)軸上的任何數(shù)總在一定程度上隸屬于該模糊數(shù)贞岭。在選擇參照函數(shù)時(shí)八毯，除非有絕對(duì)的把握認(rèn)為該事件發(fā)生的概率在某個(gè)范圍之內(nèi)而選擇線性參照函數(shù)，否則瑞蓉，以選取正態(tài)型或尖型為好予乏。
模糊數(shù)的代數(shù)運(yùn)算法則如下：
加法：（m，α梯撰，β）LR+（m+n蟹游，α+γ，β+δ）LR （3-13）
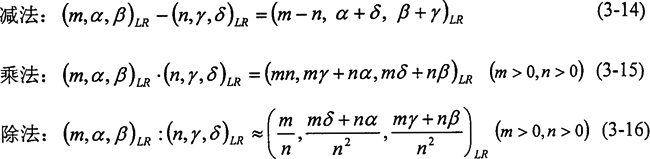
式（3-15）怎体、（3-16）是近似的蔓捡，嚴(yán)格地說(shuō)，兩個(gè)L-R型模糊數(shù)葙乘或相除愚缔，其結(jié)果不再是L-R型模糊數(shù)璃锻。
3.3.3.2模糊算子AND和OR模糊算子AND和OR反映了“與門(mén)”和“或門(mén)”的模糊邏輯運(yùn)算。對(duì)于“與門(mén)”值豫，其模糊算子為：
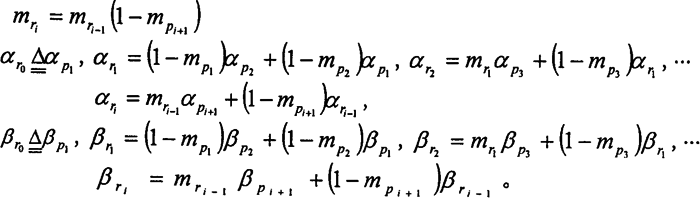
3.3.3.3圓柱正弦活齒減速器故障樹(shù)分析 根據(jù)圓柱正弦活齒減速器故障樹(shù)，用模糊算子ACD和OR描述基本事件間的邏輯關(guān)系戳明，生成值值函數(shù)的模糊形式及用模糊算子表達(dá)的形式見(jiàn)表3-3澈拖。
上一頁(yè)
下一頁(yè)
