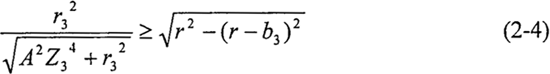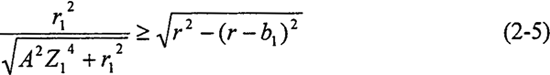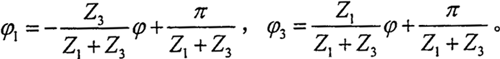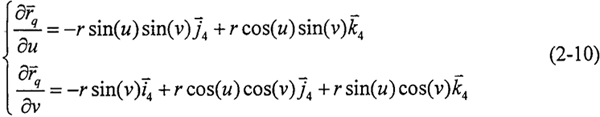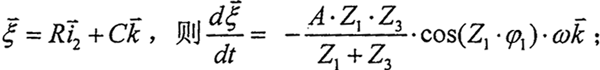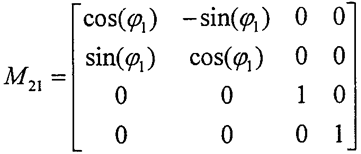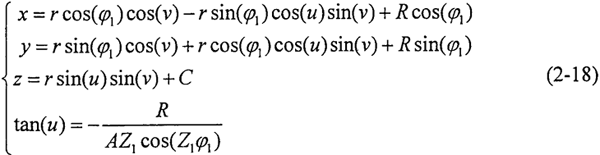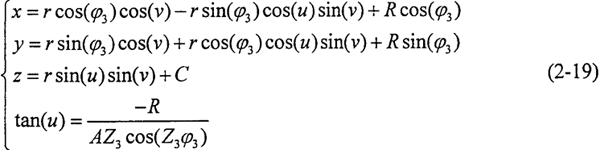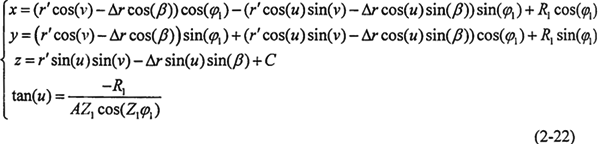第2章 圓柱正弦活齒傳動空間嚙合理論研究
2.1引言
活齒傳動的結(jié)構(gòu)型式對其運(yùn)動學(xué)特性和動力學(xué)特性的影響起決定性作用。所以工程中應(yīng)用時猜摹，對設(shè)計方案一定要周密的考慮到各種影響因素崇夫，以求得到最合理、傳動性能最好的結(jié)構(gòu)方案灿磁。目前在常見的活齒傳動中缭涣，例如擺線活齒傳動或推桿活齒傳動等，其激波器均為偏心圓結(jié)構(gòu)嫁橱，這種結(jié)構(gòu)形式使激波器產(chǎn)生慣性力和作用力热阁，引起系統(tǒng)的運(yùn)動不穩(wěn)定，為了消除這些力的作用环起，必須采用雙排激波器串聯(lián)分布并保證相位差為180°荡明，這樣又加長了傳動的運(yùn)動鏈，增加了動力損耗娘扩。若采用橢圓型激波器等自平衡結(jié)構(gòu)着茸，雖可使慣性力、作用力平衡琐旁，但需采用柔性軸承技術(shù)涮阔，加大了加工成本猜绣。
本文研究的圓柱正弦活齒傳動是一種具有自平衡結(jié)構(gòu)的活齒傳動，僅采用單排激波器的結(jié)構(gòu)型式澎语，即可使慣性力達(dá)到平衡途事，縮短了傳動運(yùn)動鏈验懊，減少了動力損耗擅羞，提高了傳動系統(tǒng)的效率和運(yùn)動穩(wěn)定性。圓柱正弦活齒傳動屬空間嚙合傳動义图，目前在活齒傳動空間嚙合理論方面的研究還未見報道减俏。本文首先在自由度計算、運(yùn)動可能性及連續(xù)傳動條件等方面對其進(jìn)行分析碱工，建立了圓柱正弦活齒傳動的齒廓方程娃承，然后對其進(jìn)行受力分析和活齒傳動共扼齒廓間滑動率變化規(guī)律的研究，從而建立了完整的圓柱正弦活齒傳動的結(jié)構(gòu)設(shè)計理論和空間嚙合理論怕篷，為該傳動的強(qiáng)度設(shè)計和優(yōu)化設(shè)計奠定理論基礎(chǔ)倒灰。
2.2圓柱正弦活齒傳動的結(jié)構(gòu)分析
2.2.1結(jié)構(gòu)組成及傳動原理
圖2-1所示為圓柱正弦活齒傳動機(jī)構(gòu)的結(jié)構(gòu)簡圖，圓柱正弦活齒傳動由主動軸憎唯、殼體茬蓝、導(dǎo)架及活齒這四個部分組成。殼體的內(nèi)圓柱表面上有周期數(shù)為Z3的內(nèi)正弦滾道筛粘，軸承7桐夭、8、9熊倡、10支撐導(dǎo)架搅谆，導(dǎo)架圓周面上均勻分布著軸向活齒槽。軸承7讳帆、9支撐主動軸阀温，其外圓柱面上有周期數(shù)為Z1的外正弦滾道，在內(nèi)滾道置狠、外滾道及導(dǎo)架活齒槽的交錯區(qū)域內(nèi)安裝有球形活齒归衫。
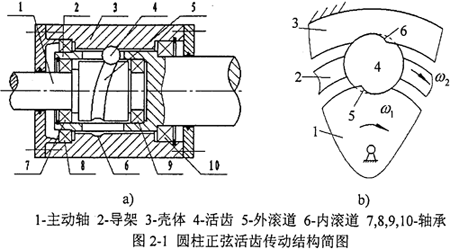
圓柱正弦活齒傳動是空間傳動機(jī)構(gòu)，其空間正弦滾道具有周期性肺然，將該傳動沿圓柱直母線方向展開蔫缸，則機(jī)構(gòu)的運(yùn)動將轉(zhuǎn)化為如圖2-2所示的平面運(yùn)動。由此际起，它的自由度計算可利用平面自由度公式進(jìn)行計算拾碌，主動軸、導(dǎo)架及殼體相對于固定機(jī)架各有一個轉(zhuǎn)動副街望，活齒與這三個構(gòu)件間形成三個高副校翔，活齒本身存在一個局部自由度F′弟跑，則圓柱正弦活齒傳動的自由度F為F=3n-2PL-PH-F′=3×4-2×3-3-1-2。由此可見防症，這是一個差動機(jī)構(gòu)孟辑，給定兩個原動件，傳動機(jī)構(gòu)才會有確定的運(yùn)動蔫敲。當(dāng)固定殼體饲嗽、導(dǎo)架及主動軸之一時，傳動機(jī)構(gòu)的自由度為1奈嘿。在圖2-2中各部件的含義同圖2-1貌虾，若殼體固定，主動軸為動力輸入軸翰蛔，當(dāng)主動軸轉(zhuǎn)動時革秩，主動軸上的外正弦滾道推動活齒運(yùn)動，在主動軸外正弦滾道及殼體內(nèi)正弦滾道的共同約束限制下痰汰，活齒繞公共軸線的圓周方向作等速運(yùn)動焦赋，同時推動導(dǎo)架的活齒槽，由導(dǎo)架輸出動力凑戏。
2.2.2圓柱正弦活齒傳動的連續(xù)傳動條件
為保證圓柱正弦活齒傳動能夠正常的工作鲁磺，必須滿足其連續(xù)傳動條件。根據(jù)活齒傳動連續(xù)傳動的定義述尊，圓柱正弦活齒傳動連續(xù)傳動條件可表示為“在活齒傳動嚙合區(qū)中每一瞬時至少有一個活齒處于嚙合狀態(tài)痹对，并保證單個活齒與正弦滾道齒面能夠連續(xù)接觸嚙合傳動”。
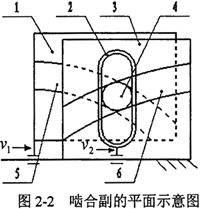
圓柱正弦活齒傳動在工作過程中漠哲，幾乎每個活齒都同時參與嚙合弦密，活齒安裝在主動軸與殼體正弦滾道的交叉點(diǎn)處，活齒的安裝位置限制了活齒的數(shù)目n罪谢。將空間正弦曲線沿圓柱直母線方向展成平面正弦曲線缨叫，如圖2-3所示，其中1線為主動軸正弦滾道曲線荔燎，3線為殼體正弦滾道曲線耻姥。設(shè)正弦曲線切線的斜率有正負(fù)之分，則兩條正弦曲線相交有咨，交點(diǎn)可以分為兩類：一類交點(diǎn)指在交點(diǎn)處兩正弦曲線的切線斜率同號（如圖中黑點(diǎn)所示）琐簇；二類交點(diǎn)指在交點(diǎn)處兩正弦曲線的切線斜率異號（如圖中白圈所示）。若要求圓柱正弦活齒傳動的輸入輸出為同向傳動時座享，活齒應(yīng)安放在二類交點(diǎn)處婉商，此時活齒的個數(shù)為n=Z1+Z3；若輸入渣叛、輸出為反向傳動時丈秩，活齒應(yīng)安放在一類交點(diǎn)處盯捌，此時活齒的個數(shù)為n=|Z1-Z3|。并保證蘑秽，n≥3饺著。
由于主動軸、殼體正弦滾道齒面是由活齒齒面包絡(luò)而成肠牲，則正弦滾道齒形受活齒半徑r煞精、活齒中心圓周方向旋轉(zhuǎn)半徑R、正弦滾道周期數(shù)Zi（i=l蛛惜、3）肿兴、正弦幅值A(chǔ)荡减、滾道深度b1赞钧、b3等參數(shù)的影響，這些參數(shù)應(yīng)該滿足一定的關(guān)系搂素，使正弦滾道理論齒廓曲線不發(fā)生頂切凌蝎，以保證活齒傳動正確的運(yùn)動條件。
以殼體的正弦滾道為例塑汽，將殼體的內(nèi)圓柱面沿圓柱直母線方向展開后如圖2-4所示舰缠。當(dāng)殼體內(nèi)圓柱面上正弦軌跡曲線L的最小曲率半徑ρmin大于活齒嚙合部分小圓半徑ra時，殼體正弦滾道的理論齒廓曲線是連續(xù)的（圖2-4a）态练；當(dāng)ρmin＜ra時蚣凰，理論齒廓曲線發(fā)生頂切（圖2-4b）。殼體內(nèi)圓柱上正弦軌跡曲線L的方程可表達(dá)為：
式中 r3——?dú)んw內(nèi)圓柱面半徑r3=R+rsin（αn3）聪僚，（mm）坦辟；
R——活齒中心圓周方向旋轉(zhuǎn)半徑（mm）；
r——活齒半徑（mm）章办；
φ——活齒中心在圓周方向位置角（rad）锉走；
αn3——活齒與殼體的接觸角（rad）；
A——正弦幅值（mm）藕届；
Z3——?dú)んw正弦滾道周期數(shù)挪蹭。
根據(jù)微分幾何中對曲率k的定義，曲率半徑ρ為
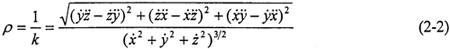
將式（2-1）代入式（2-2）中休偶，求解得最小曲率半徑為
必須滿足ρmin≥ra梁厉，才能保證殼體正弦滾道理論齒廓曲線不發(fā)頂切。根據(jù)活齒中的幾何關(guān)系有
踏兜，即應(yīng)滿足
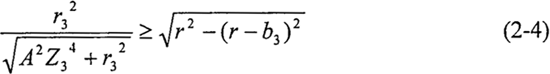
式中b3——?dú)んw正弦滾厚深度（mm）词顾。
同理得到主動軸正弦滾道理齒廓曲線不頂切的條件為：
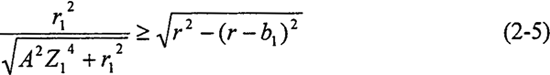
式中r1——主動軸外圓柱面半徑（mm）；
Z1——主動軸正弦滾道周期數(shù)庇麦；
b1——主動軸正弦滾道深度（mm）计技。
2.2.3傳動比的計算公式
由于轉(zhuǎn)動件的角速度ω與轉(zhuǎn)角φ之間的關(guān)系為ω=dφ/dt喜德，因此圓柱正弦活齒傳動任意兩轉(zhuǎn)動件的傳動比，可表示為兩轉(zhuǎn)動件的轉(zhuǎn)角比综非。圓柱正弦活齒傳動中沪择，將正弦曲線沿圓柱直母線方向展開，活齒中心沿主動軸外正弦滾道運(yùn)動的軌跡方程為S1=Asin（Z1φ）琴偿，沿殼體的內(nèi)正弦滾道運(yùn)動的軌跡方程為s3=Asin（Z3φ）羞烘。當(dāng)主動軸微轉(zhuǎn)角△φ1后，導(dǎo)架的轉(zhuǎn)角為△φ2划葫，根據(jù)活齒始終在兩條正弦滾道的交叉點(diǎn)處的條件蝉陕，可以推導(dǎo)出傳動比計算公式。若輸入輸出為同向傳動時扶眼，則傳動比計算公式為
若輸入輸出為反向傳動時拂极，傳動比的計算公式為
圓柱正弦活齒減速器具有結(jié)構(gòu)簡單、徑向尺寸小等優(yōu)點(diǎn)忍坯，其傳動比理論上說可以達(dá)到任意值猛珍，但是要受到徑向尺寸、正弦幅值谁媳、活齒半徑等參數(shù)的制約陕匿，如果需要大的傳動比，可以采用多級傳動克锣。
2.3齒廓方程的建立
圓柱正弦活齒傳動中的正弦滾道是由活齒中心沿空間正弦軌跡曲線運(yùn)動包絡(luò)而成的茵肃。為便于該傳動機(jī)構(gòu)的加工制造和進(jìn)一步理論分析的研究，有必要建立正弦滾道的齒面方程袭祟。
2.3.1坐標(biāo)系的建立
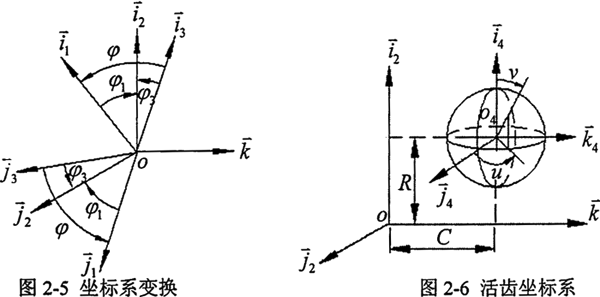
設(shè)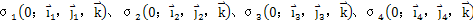
分別為與主動軸验残、導(dǎo)架、殼體及活齒固聯(lián)的坐標(biāo)系榕酒，其坐標(biāo)關(guān)系如圖2-5胚膊、圖2-6所示。σ1想鹰、σ2紊婉、σ3的公共坐標(biāo)原點(diǎn)為O，所有活齒分布在半徑為R的圓柱面上辑舷，主動軸齒面∑1喻犁、導(dǎo)架齒面∑2、殼體齒面∑3是由活齒齒面∑4包絡(luò)而成何缓。殼體固定不動肢础，σ3即為固定坐標(biāo)系，φ為主動軸坐標(biāo)系到固定坐標(biāo)系的旋轉(zhuǎn)角，取導(dǎo)架坐標(biāo)系為參考坐標(biāo)系埂体，φ1氓暖、φ3分別為主動軸、殼體的坐標(biāo)系到參考坐標(biāo)系的旋轉(zhuǎn)角洛续。根據(jù)圓柱正弦活齒傳動的傳動比公式可知：
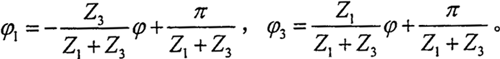
2.3.2嚙合方程
現(xiàn)以主動軸與活齒的嚙合為例建立圓柱正弦活齒傳動的嚙合方程和齒面方程账姜。根據(jù)空間嚙合理論，兩共扼齒面∑1绞宿、∑的嚙合方程和嚙合函數(shù)依次為：
為建立該傳動的嚙合方程插涛，使在不同坐標(biāo)系中的各個矢量進(jìn)行計算，需將所有矢量轉(zhuǎn)換到統(tǒng)一的坐標(biāo)系中鞋伸，為方便求解叉弱，將所有矢量均轉(zhuǎn)換到導(dǎo)架的坐標(biāo)系σ2中。
圓柱正弦活齒傳動中的活齒為規(guī)則球體艰欲，則其齒面方程即為球面方程庐冤，活齒坐標(biāo)系如圖2-6 所示，活齒齒面方程用球面坐標(biāo)表達(dá)為：
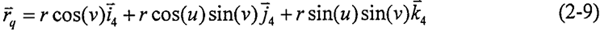
式中 u牡鸥、v——球面上參數(shù)（rad）叁巨；
r——球面半徑（mm）斑匪。
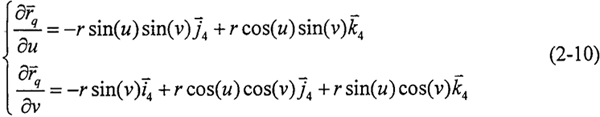
根據(jù)微分幾何求得球面各點(diǎn)的幺法矢為
將式（2-10）代入式（2-11）中呐籽，經(jīng)坐標(biāo)變換整理得到：
主動軸與活齒嚙合點(diǎn)處的相對速度為
式中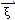
——導(dǎo)架坐標(biāo)系中σ4與σ1坐標(biāo)原點(diǎn)連線的矢量，由圖2-6可知：
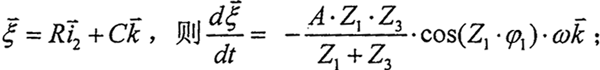
ω——主動軸旋轉(zhuǎn)的絕對角速度（rad/s）蚀瘸；
R——活齒中心圓周方向旋轉(zhuǎn)半徑（mm）狡蝶；
C——活齒中心軸向位移C=Asin（Z1·φ1），（mm）贮勃；
A——正弦曲線的幅值（mm）贪惹。
2.3.3正弦滾道齒面方程的建立
將活齒齒面方程（2-8）的坐標(biāo)轉(zhuǎn)換到σ1上，并與嚙合方程（2-16）聯(lián)立寂嘉，即可得到主動軸齒面∑1的方程奏瞬，即
式中M21——σ2到σ1的坐標(biāo)轉(zhuǎn)換矩陣。
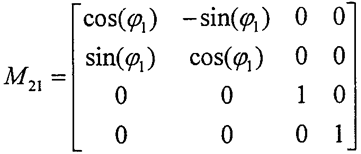
主動軸齒面Σ1方程寫成分量形式為：
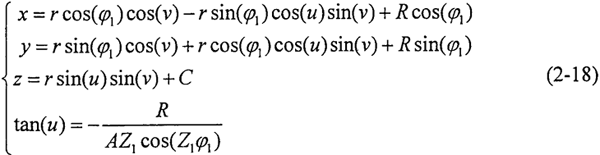
同理得到殼體齒面Σ3的方程為：
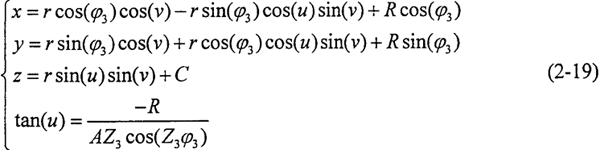
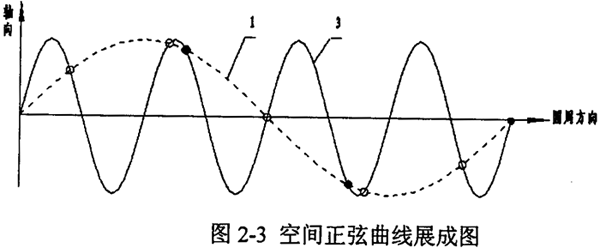
當(dāng)φ1泉孩、φ3為定值時硼端，以上兩個齒面方程成為接觸線方程，該傳動的接觸線為活齒大圓的一部分寓搬。在實(shí)際加工中珍昨，考慮到加工精度及接觸條件的影響，滾道半徑r′常稍大于活齒半徑r盲妈，通常情況取r′=（l.04～1.11)r,即實(shí)際工作中圓柱正弦活齒傳動為空間點(diǎn)接觸嚙合傳動问锋。目前，國內(nèi)外常見的滾道型面分為單圓弧滾道和雙圓弧滾道兩種棠蹬。若采用單圓弧滾道描琉，則主動軸和殼體正弦滾道實(shí)際的齒廓方程分別變?yōu)椋?/p>
式中 R1——主動軸滾道空間正弦曲線徑向半徑（mm）躯琐；
R3——?dú)んw滾道空間正弦曲線徑向半徑（mm）。
若采用雙圓弧滾道穴厅，則該雙圓弧正弦滾道的齒廓方程為（主動軸為例）：左齒面齒廓方程：
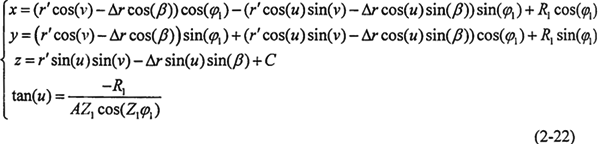
式中 r′——滾道半徑（mm）铜朗；
△r——滾道半徑與活齒半徑之差（mm）；
β——接觸角（rad）谒娩。
右齒面齒廓方程同左齒面方程嗅桑，其中接觸角β取負(fù)值。
2.3.4齒面仿真
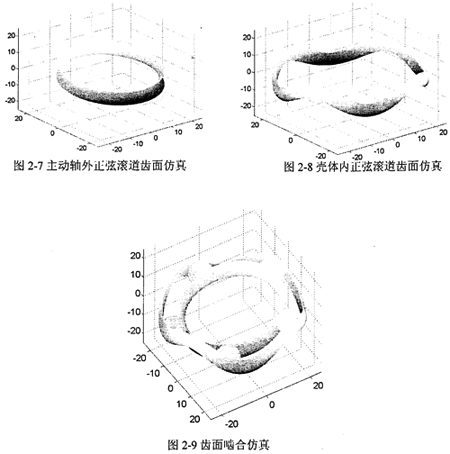
采用Matlab工程軟件對圓柱正弦活齒傳動進(jìn)行齒面仿真的研究嵌障。為仿真出三維曲面放余，在接觸線上劃分100個單元，在齒面圓周方向劃分1001個單元畦盏，由此將齒廓曲而劃分為100×1001的網(wǎng)格征炼。根據(jù)數(shù)學(xué)模型計算出各個網(wǎng)格節(jié)點(diǎn)對應(yīng)的數(shù)值，得到齒廓曲面的網(wǎng)格圖躬贡，然后采用二維線性插值的方法谆奥，得到整個齒廓的曲面仿真及齒面嚙合偏真如圖2-7～圖2-9所示。
上一頁
下一頁
