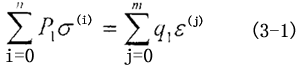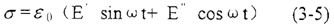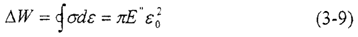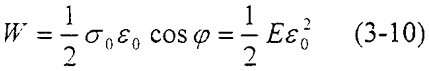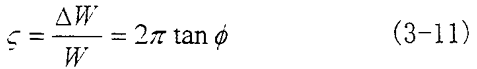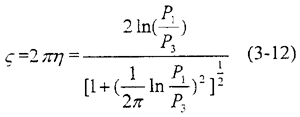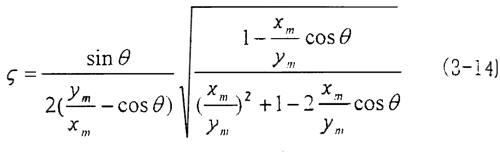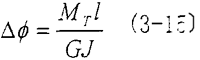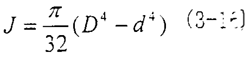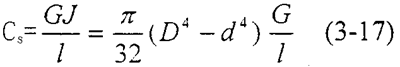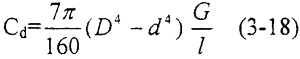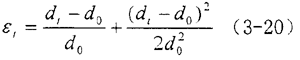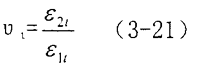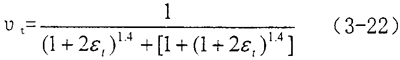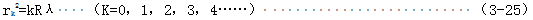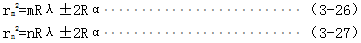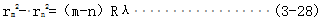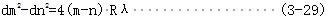|
第3 章扭振的理論計算
3.1 振動的概念
所謂振動,就是物體或某種狀態(tài)隨著時間往復變化的現(xiàn)象扇商。這類現(xiàn)象有的是由于其本身的特性等固有的原因引起的撼烹,有的是外界干擾引起的,比如溫度姐硬,沖擊等察遇。在自然界中廣泛存在著聲、光柄豹、電磁波等廣義的振動現(xiàn)象遍挚。在工程界,地面上的汽車橱狗、火車齐梆、拖拉機;地下的鐵道:天空中的飛機夭私、宇宙飛船舷咆;海洋里的艦船、海洋平臺等普遍存在著機械振動。在生物界唐唉,心臟的跳動唠鹅,肺的呼吸,肌肉的顫動酌摇,腦電波的脈動等等在某種意義上來說膝舅,都是一種振動.振動是自然界最普遍的現(xiàn)象之一。
發(fā)生振動的機器或結構物等都稱為振動系統(tǒng)窑多。實際振動系統(tǒng)往往是很復雜的铸史,因此在開始研究問題時,總要把研究對象以及外界對它的作用簡化為一個理想的力學模型怯伊、這個力學模型往往由質量塊琳轿、彈性件和阻尼件組成。質量意味著存在慣性耿芹,即系統(tǒng)經(jīng)過平衡位置時停不下來還要繼續(xù)往前運動:彈性則意味著質量塊要被拉回到平衡位置上崭篡。彈性和慣性結合在一起就會發(fā)生振動。阻尼元件則使振動受到一定程度的抑制吧秕。由此可見琉闪,質量塊、彈性元件和阻尼元件等是振動系統(tǒng)中的主要元件砸彬,它們不同的組合而構成的理想模型可以代替各種實際研究時象颠毙。有了這樣力學模型,對干理論計算或模擬試驗都帶來了方便蓉凰。
3.2 扭轉振動的機理
引起彈性聯(lián)軸器扭轉振動的原因主要歸結于兩個方面:即由柴油機引起的機械擾動和由發(fā)電機引起的電氣擾動芳窟。
3.2.1 柴油機引起的機械擾動
柴油機本身在運行過程中,由于軸系本身不僅具有慣性而且還具有彈性酬绞,加上作用在軸系上的周期性的干擾力矩的作用抬爷,使軸段產(chǎn)生周向交變及相應的變形,從而使軸系具有扭振的特性祖务。干擾力矩包括柴油機工作時汽缸內(nèi)氣體壓力Pg變化而產(chǎn)生周期性的激勵力矩留嫩,這是引起扭振的主要原因。柴油機曲柄連桿機構運動時的慣性力產(chǎn)生的力矩也是激勵力矩的一部分彭撑。柴油機運動部件運動時絮檀,可產(chǎn)生由重力造成的和有慣性力造成的激勵力矩:運動部件的慣性力包括離心慣性力和往復慣性力。離心慣性力是不產(chǎn)生扭振激勵的蜈藏,往復慣性力會產(chǎn)生周期性變化的激勵扭矩卜陵。
柴油機氣缸內(nèi)工質燃燒期間,氣體力是一脈沖載荷蓝垢,急速燃燒期的壓力升高率對其頻充特性有重大影響挑乓,當出現(xiàn)氣缸工作工程故障時女责,例如進氣壓力不正常漆枚,噴油提前角未調準创译,燃油霧化質量不良,各缸噴油量不均勻等都會對其他脈沖的起始壓力墙基,壓力升高率软族,最高爆發(fā)壓力,脈沖的作用時間造成影響残制,使單缸激勵力矩的幅值立砸,頻率和相位均有變化,導致各缸激勵力矩合成結果的變化初茶,而且此時各缸負荷不均勻颗祝,各氣缸產(chǎn)生的各諧次的激勵力矩的幅值和相位彼此不相等,這個也會造成扭轉振動恼布。
另外螺戳,一些柴油機故障,如燃燒不足折汞、某缸停缸倔幼、減振器損壞、曲軸驅動的其它附屬系統(tǒng)的損壞等也會產(chǎn)生扭轉振動整诈。
3.2.2 發(fā)電機引起的電氣擾動
包括發(fā)電機在內(nèi)的電氣系統(tǒng)坷磷,在發(fā)生故障或進行某些操作時,電磁力矩可能發(fā)生突變或振蕩恒晋,激起聯(lián)軸器的扭振竹坝。
電力系統(tǒng)中最常見的故障之一就是短路,短路電流可能達到上萬安培甚至幾十萬安培止歇。強大的電流除了產(chǎn)生熱和力的作用使電氣設備損壞外鹰个,還將形成不同頻率的扭矩沖擊。這是因為在短暫的時間內(nèi)场暮,柴油機調節(jié)系統(tǒng)不可能調整好柴油機和發(fā)電機之間的功率骏拱,不可能使之達到平衡。短路的類型有三種:三相短路迁枪、兩相短路和單相短路(或兩相接地短路)难圣。前一種為對稱短路,出線端三相短路所造成的后果最為嚴重冲肖。后兩種為不對稱短路们豌。
3.2.3 其他原因造成的扭振動
安裝時在聯(lián)軸器所聯(lián)接的軸不對中的情況下,會產(chǎn)生一個附加應力浅妆,從而產(chǎn)生附加扭矩望迎,造成聯(lián)軸器的扭振現(xiàn)象。
另外,由于環(huán)境的影響或者旋轉時候的摩擦辩尊,產(chǎn)生大量的熱能涛浙,熱應力也會促使聯(lián)軸器出現(xiàn)扭振現(xiàn)象,影響聯(lián)軸器的工作狀態(tài)和使用壽命摄欲。
3.3扭轉振動特性模型
在扭轉振動特性(包括固有頻率和振型)的計算中轿亮,常用的模型主要有兩種:集中質量模型和連續(xù)質量模型。前者又可以分為簡單集中質量模型和多單元集中質量模型胸墙。
3.3.1 集中質量模型
集中質量模型我注,是將研究對象分解成若干集中質量塊,相鄰質量塊之間用無質量的理想彈簧聯(lián)結迟隅,形成一種多質量一彈簧系統(tǒng)但骨。根據(jù)分塊數(shù)的多少又可以分為簡單集中質量模型和多單元集中質量模型。由于分塊數(shù)的多少決定著計算的精度智袭,簡單集中質量模型雖然可以對研究對象低階特性進行精確的描述董纺,但由于其本身階數(shù)很低,無法體現(xiàn)研究對象較高頻率模態(tài)宫氛,所以這種模型一般只用作定性分析吆律。多單元集中質量模型本質上與簡單集中質量模型相同,但是它根據(jù)研究對象的結構特點大大增加了分塊數(shù)间渐,不僅可以計算研究對象的低階特性妈务,在計算研究對象高階特性時也可以有很高的精度。其缺點是當階數(shù)較高時計算量太大东哀,計算耗時長钓宗,計算精度也會由于計算中出現(xiàn)的累積誤差而降低。
針對這些問題尘斧,有關學者提出用各種降階方法构胰,如最優(yōu)Hankel范數(shù)降階法、平衡降階法等派男,在保證計算精度的前提下莱衍,降低模型階數(shù)。也有采用基于最小二乘法和軌跡靈敏度理論的參數(shù)辨識法帮寻,對給定階數(shù)的研究對象模型進行剛性系數(shù)和慣性系數(shù)的辨識乍狐。這些方法各有優(yōu)缺點,在不同的程度上解決了高階集中質量模型的問題固逗,但由于涉及理論較為復雜浅蚪,有些降階方法更是以降低精度作為代價的。此外烫罩,集中質量模型忽略了某些剛性元件的撓性惜傲,不能處理這些剛性元件的復合振動洽故。這些都限制了多單元集中質量模型的應用。
3.3.2 分布質量模型
如果研究對象本身就是一個具有分布參數(shù)的連續(xù)體盗誊,分布質量模型正是其精確描述时甚。這種模型采用偏微分方程的形式表示,既能準確地計算研究對象低階頻率和振型.也可計算高階頻率和振型浊伙。還可分析某些剛性元件撓性對扭振的影響。與集中質量模型相比长捧,分布質量模型可以很方便地計算轉軸任意截面的內(nèi)扭矩嚣鄙,適時地搜索出扭應力最危險的截面位置。由于在進行研究對象的分布質量建模時秩纹,將附屬元件等轉化為附加轉動慣量加以考慮幔时,因此這種模型可以分析附屬元件撓性對扭振的影響。因此在進行扭振響應的精確計算時园撵,可以選擇研究對象的低階分布質量模型茉油。高階分布質量模型也存在計算量比較大的問題,可以通過模態(tài)舍階降階法進行降階處理石沸。近年來有學者提出一種更為精確的低階分布質量模型一一四端網(wǎng)絡模型桨农,此算法簡便快捷,通過改進的四端網(wǎng)絡模型還可以充分考慮阻尼和附加轉動慣量對扭振的影響庵动。
3.4阻尼系數(shù)的確定
3.4.1基本模型
對于任意粘彈性材料來說捍刑,其一般的本構關系都可寫成如下形式:
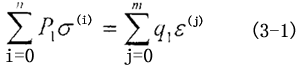
式中σ—應力
ε一應變
σ(i)一應力的i階導數(shù)(i階應力率)
ε(j)一應力的j階導數(shù)(j 階應力率)
P1,q1——常系數(shù)
從根本上說,橡膠及其增強橡膠材料都具有非線性粘彈性的性質暮课,但非線性方程在工程應用中有很大的困難法洼,故而一般使用線性粘彈性表選形式。
像膠材料在玻璃態(tài)轉化點附近表現(xiàn)出較好的線性粘彈性椎吼,而在較高的溫度區(qū)內(nèi)眠琴,則表現(xiàn)出強烈的非線性粘彈性。
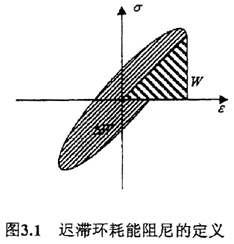
粘彈性材料在簡諧波交變動態(tài)載荷作用下姓建,應變滯后于應力一個相角φ诞仓,因此在一個循環(huán)周期內(nèi),應力應變遲滯回線為—標準的旋轉橢圓速兔,如下圖3.1所示狂芋,這一橢圓回線的面積△W代表了材料阻尼能力大小,即單位體積耗散的能量憨栽,三角形面積W為材料所儲存的最大彈性能密度帜矾。
若給定應變激勵為

則應力響應函數(shù)為:

如果以復數(shù)形式表征

展開(3-3)式有:
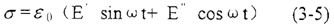
式中E-材料的彈性模量
E-儲存模量

E-耗能模量

滯后角

單位體積耗散的能量△W
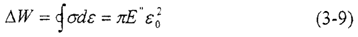
單位體積最大彈性儲能
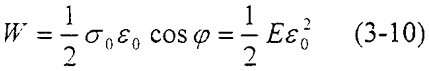
阻尼系數(shù):
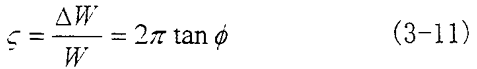
從(3-11) 式可以看出,如果能測出耗能面積ΔW或應變應力的滯后角φ屑柔,就可以測定阻尼系數(shù)屡萤。
3.4.2測量方法
(1)自由振動法測阻尼系數(shù)
對于粘彈性材料來說珍剑,由于具有粘滯性,其自由振動表現(xiàn)為一衰減波形式死陆。通過分析其峰值包絡線招拙,即可得到阻尼系數(shù)。
圖3.2為自由振動法的測量裝置示意圖措译。
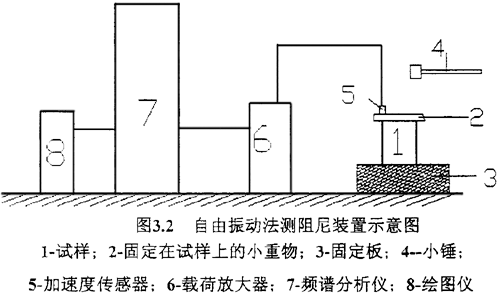
試樣在被輕輕錘擊所產(chǎn)生自由阻尼振動别凤,其加速度信號通過載荷放大器輸入頻譜分析儀,經(jīng)兩次積分后得出位移衰減曲線翼辱,如下圖3.3所示乃描。可得出春滯后阻尼系數(shù)吴烹。
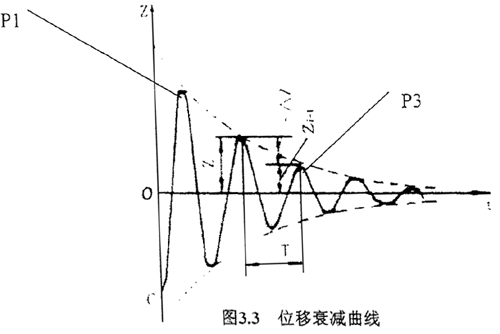
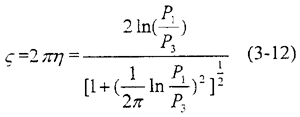
式中P1斯凑,P3—圖3.3中標明的曲線峰值,ζ稱為耗能因子
實際上眨攀,由于振動的隨機性蛀颓,其曲線峰值亦具有隨機性,滯后阻尼系數(shù)可通過最小二乘法求包絡線方程y=pexp(-ηωnt)出扛聂。式中y為位移艘尊,ωn為固有頻率。
(2)強迫振動法測阻尼系數(shù)
用自由振動法測滯后的阻尼系數(shù)時栏付,難以考慮溫度及應變率對其的影響影晋。而使用強迫振動法測可計入溫度及應變率的影響。對于給定的試樣毕删,先預加一初應變镜会,然后加一受控的正弦應變波,使試樣做拉一拉運動(始終保持正應變)终抽,預應變以保持加載過程中試樣不受壓力為準戳表。通過這個實驗,可以得到材料的應力—應變曲線的滯后圈昼伴,并可得到循環(huán)加載的次數(shù)對滯后圈的影響匾旭。根據(jù)前文所提出的滯后損失與應變能的關系,即可得到材料的阻尼系數(shù)圃郊。
(3)半功率點法
由振動理論知价涝,一個振動系統(tǒng)的能量是與其振幅的平方成正比。系統(tǒng)強迫振動的能量在共振點前后能量為共振時能量的1/2處的兩個頻率f1持舆、f2稱為半功率點頻率色瘩,則此半功率點頻率這差值與系統(tǒng)的阻尼比之間有如下關系

測試件阻尼系數(shù)

(4)李沙育圖法
當被測的阻尼較大時,幅頻性曲線和峰值變得不明顯或甚至不出現(xiàn)逸寓,這時可用李沙育圖法居兆。該法的測量系統(tǒng)3.5所示
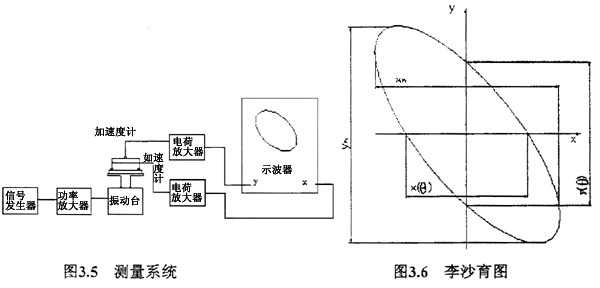
將試件固定在振動臺上受激振動覆山。如測振動臺面振動的加速度計、電荷放大器和示波器的X軸組成的測量系統(tǒng)與測被測對象振動的加速度計泥栖、電荷放大器和示波器y軸組成的測量系統(tǒng)福互,兩者在幅頻特性和相頻特性上完全一致。
則試件阻尼系數(shù)
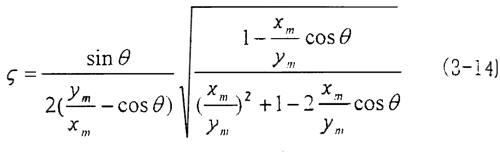
參考前人的研究數(shù)據(jù)和以上的實驗方法厨刷,再綜合實際測量的結果鹉鉴,我們將橡膠聯(lián)軸器的阻尼系數(shù)定為0.2。
3.5動剛度的確定
從材料力學中可知糙枚,對于一根等截面長度為1彪选,材料的剪切模量為G的圓柱軸段,當兩商加一扭矩MT時院蜘,則軸段兩端的盯對扭轉角位移為:
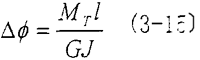
式中J——模截面的極慣性矩所讶,對于空心圓軸狀的元件
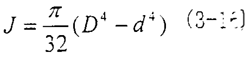
式中D—空心圓截面半徑m
d—空心圓截面內(nèi)徑m
材料的扭轉剛度表示等直徑軸扭轉單位角度所需要的扭矩惊眠,用CS表示纳傍,則:
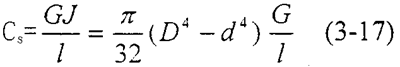
前面介紹過,在彈性聯(lián)軸器轉動過程中尖鲜,起作用的是動剛度拧亡,根據(jù)第二章討論的結果,我們?nèi)颖堵蕿?.4宣璧,用Cd表示動剛度谤碳,則
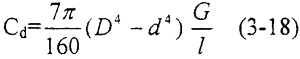
3.6 泊松比的確定
3.6.1 泊松比的定義
泊松比又稱橫向變形系數(shù),在彈性范圍內(nèi)溢豆,材料不論受拉或受壓蜒简,其值等于側向應變與軸向應變之比值,用υ表示漩仙,即

泊松比無因次量搓茬,是表示材料物理性質的一個彈性常數(shù)。它是以法國力學家S.D.Poisson (1781-1840)命名的队他。
3.6.2 泊松比的測量
由于橡膠材料剛度較小卷仑,采用接觸式的測量方法會增加橡膠表面剛度,使橡膠拉伸變形失真麸折,給材料的應變測量帶來很大的誤差锡凝。因此采用傳統(tǒng)的電阻應變片法和云紋法等接觸式測量方法已經(jīng)不能準確地測定橡膠材料的拉伸變形。非接觸式變形測量方法很多垢啼,拉曼光譜法窜锯、電子散斑干涉法、中子衍射法等方法也已經(jīng)被采用芭析,還有采用高分辨率的電荷耦合傳感器(CCD)的3D 光學非接觸式變形測量儀測量三維變形痒仇。
(1)電荷耦合傳感器(CCD)
在橡膠單軸拉伸實驗中然那,選用十字形試樣。橡膠試樣工作區(qū)域尺寸為50mm×50mm恰印。在試樣的前后兩面各劃2條距離20mm的平行白色標記線涝沈,白線的中心位置用一維質心法來確定。以此作為靶標瓢圈,通過CCD測量系統(tǒng)比較不同時刻平行的2條白線的質心之間位移的變化
在橡膠試樣拉伸過程中侍醇,首先通過長距顯微鏡將t時刻白色標記的位置聚焦在CCD探測器上,得到的兩路位移信號通過變換電路變成電壓信號后珊场,同時由CCD傳感器送入同步驅動器子历,再由同步驅動器送入12位AD數(shù)據(jù)采集卡。單向拉伸實驗數(shù)據(jù)以時間-位移的形式被輸入計算機逼酗,通過數(shù)據(jù)處理軟件系統(tǒng)處理后稻便,就可以得到橡膠在任意時刻的應變和泊松比。
該實驗中平行的兩條白線中心之間的起始距離(d0)為20mm诽昨,拉伸t時刻時兩條平行白線中心之間的距離變?yōu)閐1趁宠,設εt為材料在t時刻的格林應變,則
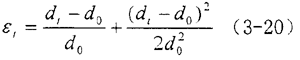
假定如果拉伸方向是1方向惜姐,垂直于拉伸的方向為2方向犁跪,則橡膠在t時刻的主泊松比(υt)為
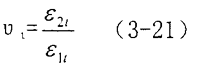
假定橡膠材料在拉伸狀態(tài)時材料變形前后體積不變,并假定在變形前后均為方形歹袁,橡膠材料在t時刻時泊松比和格林應變的關系可以通過下式確定
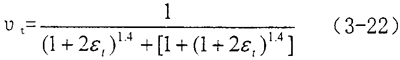
由上式可以看出橡膠材料的泊松比隨格林應變的增加而減小坷衍。
(2)光干涉式測量
如下圖3.7所示,在A条舔、B兩支點上枫耳,放一截面為矩形,長度為L的試件孟抗,兩端加外力F(集中力)迁杨,使試件產(chǎn)生無損彎曲。
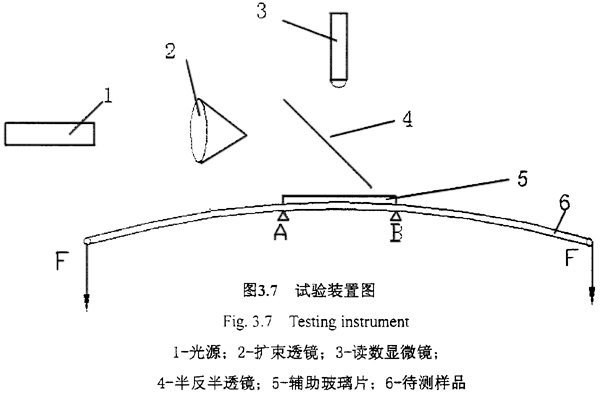
如下圖3.8所示夸浅,設ρ1表示試件中曲面與xoy面相平行的曲率半徑仑最,ρ2表示試件中曲面與yoz面相平行的曲率半徑,試件在純彎曲時沿X軸帆喇、Z軸的線應變?yōu)?/p>
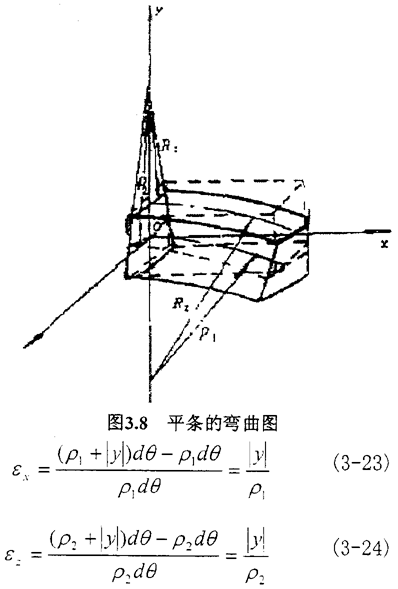
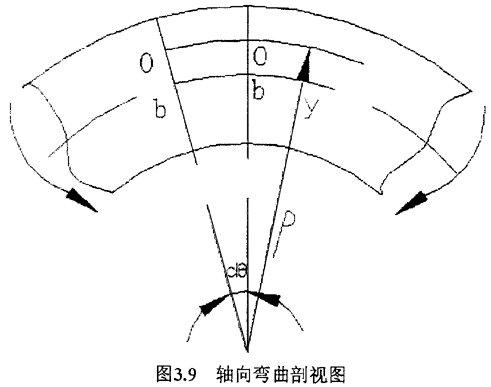
圖3.9是軸向彎曲剖視圖
在干涉式測量系統(tǒng)中警医,輔助玻璃片與變形的試件表面間形成一層薄膜。當光源經(jīng)擴束透鏡和半反透射鏡垂直照射時馁雏,入射光將在些薄膜上下表面反射酱晾,產(chǎn)生具有一定光程左的兩束相干光,產(chǎn)生一系列明暗交替的雙曲線托俯,在計數(shù)顯微鏡中將觀察到雙曲線等厚干涉條紋赠飞,如圖3.10所示拼固。
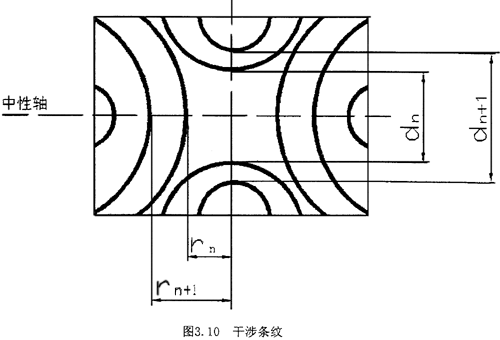
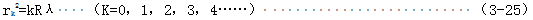
式中rk——第k級雙曲線干涉條紋頂點至中心線的距離m
假設附加厚度為n,取第m篙协,n級暗條紋今攀,則對應的雙曲線的頂點到中心線的距離為
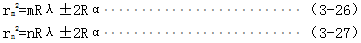
式中rm,rn—第m級粟朵、第n級雙曲線頂點到中心線的距離m
(3-27)-3-28(得)
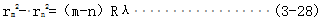
為消除干涉圖樣中心的確定而產(chǎn)生的誤差敲抄,轉換為對應的雙曲線干涉條紋兩頂點間的距離的測量,得
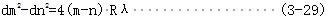
因而軸向彎曲的曲率半徑為
上一頁
下一頁
|