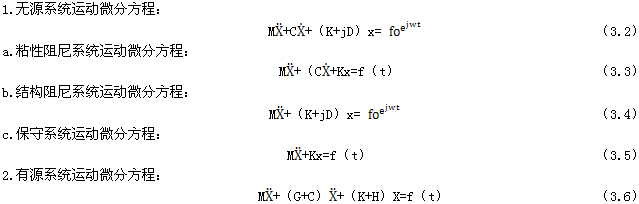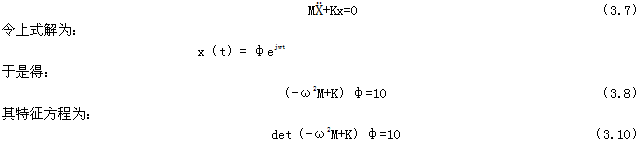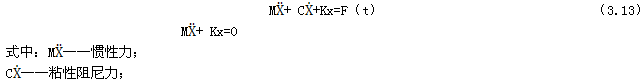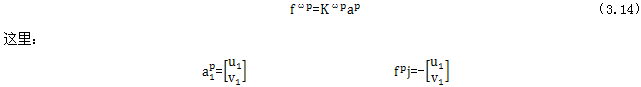第三章 三環(huán)減速器建模及動態(tài)特性有限元分析計算
§3-1 引言
對三環(huán)減速器振動系統(tǒng)進行振動與噪聲的分析與研究,首先必須建立其數(shù)學模型胶逢,數(shù)學模型有理論建模和試驗建模兩類。所謂的理論建模是指由結構挠羔、機械的設計圖紙出發(fā),作出必要的假定與簡化埋嵌,根據(jù)力學原理建模;而試驗建模是對振動系統(tǒng)進行激振俱恶,通過沒量獲得系統(tǒng)的輸入雹嗦、輸出數(shù)據(jù),再經(jīng)過對它們的分析合是、處理而建立的模型了罪。這兩類方法各有其特點,可分別適用于自己特點的情況聪全。在此泊藕,我們僅討論對三環(huán)減速器振動系統(tǒng)進行理論建模,并在SUN工作站上用I-DEAS軟件的有限元模塊及實體建模模塊對SHQ40建模并計算难礼,而試驗建模我們將在第六章中討論娃圆。
§3-2 描述振動系統(tǒng)的方法
振動系統(tǒng)有確定性和隨機系統(tǒng)兩大類,在這里涂颠,我們主要討論確定性振動系統(tǒng)固脸。確定性振動系統(tǒng)通常分為分布參數(shù)振動系統(tǒng)和離散振動兩大類,不同的振動系統(tǒng)存在其相應的描述方法俗齿。
§3-2.1 分布能數(shù)振動系統(tǒng)
具有分布質量典患、彈性和阻尼的系統(tǒng),稱為分布參數(shù)或連續(xù)參數(shù)系統(tǒng)圆滓。在域D的每一點都應滿足如下的運動微分方程猾灰。
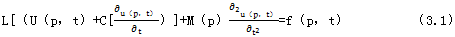
式中:U(p,t)——任意點p的位移存站,它應滿足的邊界條件是:
B萌小,[u(p,t)]=0清腌,(i=0厂均,1,2……帆摊,p)碱茁;
L—一個線性的2P階齊次數(shù)微分算子裸卫,它描述了系統(tǒng)的剛度分布;
C—一個類似于算子L的2P階線性齊次數(shù)分算子纽竣,它描述了系統(tǒng)的阻尼分布墓贿;
M—線性齊次微分算子,它描述了系統(tǒng)的質量分布蜓氨;
f(p聋袋,t)——分布激振力;
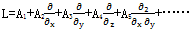
A1穴吹,A2……——坐標x幽勒,y,z的函數(shù)港令;
x啥容,y,z——p點的坐標顷霹,即p(x咪惠,y,z)淋淀;
B1——線性齊次微分算子馁胁;
由式(3.1)可知,分布參數(shù)系統(tǒng)的運動是以偏微分方程來描述的萍卑,這類運動方程中所包含的參數(shù)六主,通常是空間變量的連續(xù)函數(shù)。分布參數(shù)系統(tǒng)具有無限多個自由度辩钢。所以辉召,與一個分布參數(shù)系統(tǒng)相對應的特征解是由可數(shù)的然而是無限多個特征值和特征向量組成。
為了獲得可靠的沛三、精確的分布參系統(tǒng)的數(shù)學模型影虫,就需精確地確定運動方程中的各個參數(shù)。為此墩衍,利用如上述的試驗建模方法——振動參數(shù)識別技術是一個有效的方法跛农。通常,分布參數(shù)振動系統(tǒng)的參數(shù)識別方法有:(1)將分布參數(shù)系統(tǒng)離散化谢市,獲得離散系統(tǒng)的模型沼币,然后識別離散模型中的參數(shù)或與它相應的特征解;(2)直接以從布參數(shù)系統(tǒng)的響應識別分布參數(shù)系統(tǒng)運動微分方程中的各參數(shù)寞奸;(3)首先識別與實際分布參數(shù)系統(tǒng)相應的離散模型的特征解呛谜,然后,利用識別的特征解來識別方程中的各個參數(shù)枪萄。
一個分布參數(shù)系統(tǒng)有無限多個的特征值與特征的向量隐岛。但是猫妙,人們不可能識別完全的特征解,通常是識別與該系統(tǒng)相應的低階特征值和特征向量聚凹。此外割坠,目前的技術水平還不能滿足分布式測量的要求,因此妒牙,其識別工作還得借助于離散式測量來完成彼哼。
§3-2.2 離散振動系統(tǒng)
分布參數(shù)系統(tǒng)是一個非常復雜的系統(tǒng),它給振動分析和振動參數(shù)識別帶來了很大困難湘今,主要表現(xiàn)在:(1)系統(tǒng)的慣性敢朱、彈性、阻尼象浑、激勵力和運動都依賴于空間坐標蔫饰,因而導致數(shù)學上較難處理的偏微分方程及復雜的邊界條件。因此庸尚,一般情況下,除了少量的簡單結構外牍系,很難獲得嚴格的封閉形式的解换乙;(2)不可能獲得分布的響應測量及無限多個特征解。因而户寺,實際作振動分析膀娱、振動參數(shù)識別時,通常將無限多個自由度的分布參數(shù)系統(tǒng)離散為有限自由度的離散振動系統(tǒng)抢督。把分布參數(shù)系統(tǒng)離散化一般有以下幾種方法:
一稼注、集中質量法
把結構的質量分別集中在若干點而形成有限個質點的集中參數(shù)系統(tǒng)。質量元件喧雹、彈性元件和阻尼元件分別只有慣性栓堕、彈性和阻尼特性;
二越名、廣義坐標法
把結構的變形分解為一系列具有固定形式的函數(shù)裤爆,而以廣義坐標表示結構的變形。這種方法渺蒿,雖然理論上需要考慮無限多項痢士,但實際上只要考慮有限幾項即可獲得具有足夠精度的計算結果。如瑞利—里茲法茂装、模態(tài)坐標法等怠蹂。
三、有限元法
可以哈密頓原理導出的拉格朗日方程少态,導出離散振動系統(tǒng)的一般運動微分方程式:
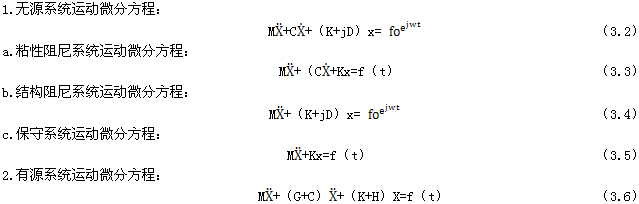
上式中:M——質量矩陣城侧,正定矩陣易遣;
C——粘性阻尼矩陣,實對稱正定式或半正定短陣赞庶;
D——結構阻尼矩陣训挡,實對稱正定式或半正定短陣;
K——剛度矩陣歧强,實對稱正定式或半定矩陣澜薄;
G=-GT——陀螺矩陣,反對稱矩陣摊册;
H=-HT——循環(huán)矩陣肤京,反對稱矩陣;
f(t)——激勵力矩陣找骏;

對于無源系統(tǒng)腿逞,當系統(tǒng)作任一運動時,D就再出現(xiàn)测捐,當振動系統(tǒng)中存在傳遞功率的曲柄汤钻、軸、滑動與裝置時法简,常形成陀螺效應和循環(huán)力荡唾,這時系統(tǒng)就成為有源系統(tǒng)。
§3-2.3 離散振動系統(tǒng)實模態(tài)坐標描述
僅討論無阻尼離散振動系統(tǒng)蓝鹿,無阻尼自由振動系統(tǒng)運動微分方程由式(3.5)確定為:
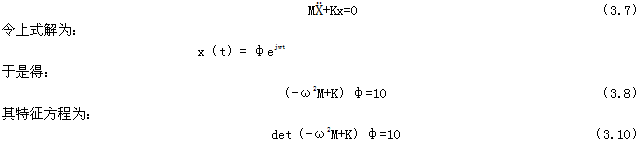
求解上式得特征值矩允,即得離散振動系統(tǒng)的固有頻率ω,然后將ω代入式(3.8)就可能解出固有振型矩陣ф贰往,則由ω赵椰、ф就構成了振動系統(tǒng)固有模態(tài)參數(shù)。由于各階固有振型ф伊厉,具有加權正交性質姜钳,且又是線性獨立的,那么就可由固有振型ф構成一個n維空間的完備的正交基镜豹,作為一個新坐標系傲须,稱之為固有模態(tài)坐標系。于是對應于原物理坐標系的任一向量x(t)趟脂,在n維空間中泰讽,可表示n階固有振型的線性組合,即:

式中q——模態(tài)位移向量昔期;
將式(3.10)代入式(3.5)已卸,再以φT前乘可得:
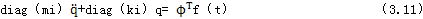
由上式可知:在實模態(tài)坐標系里,用物理坐標系描述的運動微分方程,變成n個獨立互不耦合的動運微分方程累澡。解式(3.11)可確定q梦抢,再由式(3.10)可確定物理坐標系下的響應X(t)。式(3.10)是物理坐標系和固有模態(tài)和固有模態(tài)坐標系之間相互轉換的重要關系式愧哟。
§3-3 三環(huán)減速器振動系統(tǒng)的數(shù)學模型
根據(jù)三環(huán)減速器的結構原理奥吩,如圖2-3(a)(b)和圖2-4(a)(b)所示。我們將其振動系統(tǒng)數(shù)學模型建立如圖3-0所示蕊梧。
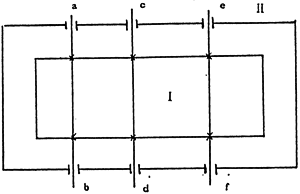
圖3-0 三環(huán)減速器振動系統(tǒng)教學模型
該模型由Ⅰ划搓、Ⅱ兩個子模型組成,其中Ⅰ子模型為傳動鏈及其附件部分配亮,Ⅱ子模型為箱體部分验脐。Ⅰ、Ⅱ子模型間通過軸與軸承在a增荐、b织活、c、d贯森、e稼那、f處緊密聯(lián)接而構成三環(huán)減速器振動系統(tǒng)數(shù)學模型。
Ⅰ沛目、Ⅱ子模型振動系統(tǒng)都是由分布參數(shù)振動系統(tǒng)页镜,它們實際的數(shù)學模型應曲式(3.1)來描述,但在實際作振動分析答肤、振動參數(shù)識別時,我們將Ⅰ瘾显、Ⅱ兩個子模型都作為離散振動系統(tǒng)來考慮愧杯,即由式(3.2)~(3.6)來確定其相應的數(shù)學模型。
一鞋既、Ⅰ子模型振動系統(tǒng)數(shù)學模型
由圖2-2力九、圖2-3(a)(b)及圖3-0分析知,Ⅰ子模型主要為傳動鏈及其附件邑闺,用于傳遞系統(tǒng)的運動和動力跌前,分析其傳動結構及原理,根據(jù)式(3.2)可得Ⅰ子模型的數(shù)學模型為:
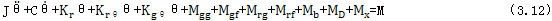

Krθ——軸陡舅、環(huán)板彈性矩抵乓;
Krθθ——各聯(lián)接處彈性矩;
Kgθθ——輪齒彈性矩靶衍;
Mgg——由齒形識別差引起的力矩灾炭;
Mgf——由齒面摩擦力引起的力矩;
Mrf——各聯(lián)接處的摩擦力矩颅眶;
Mb——軸承非線性剛度引起的彈性矩蜈出;
MD——傳動鏈中軸承阻尼力田弥;
Mx——雙曲柄機構額外沖擊力矩;
M——外界激勵力矩净处;
式中Mx的成因及其對Ⅰ子模造成的影響在第二章中已有論述安仁。
二、Ⅱ子模型振動系統(tǒng)數(shù)學模型
由圖2-2婉固、圖2-3(a)(b)及其圖3-0分析知吠童,Ⅱ子模型為箱體結構,顯然Ⅱ子模型為無源振動系統(tǒng)铸烈,故可根據(jù)式(3.2)湿颅、(3.3)、(3.4)揽宵、(3.5)知其數(shù)學模型為
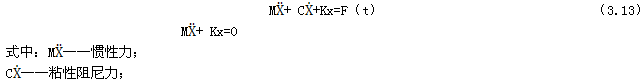
Kx——彈性力倾莽;
F(t)——外界激勵力;
三且险、Ⅰ垢雨、Ⅱ子模型間關系
由圖3-0所知,Ⅰ敛旗、Ⅱ子模型間在a辐践、b、c库说、d狂鞋、e、f處緊密相連潜的,Ⅱ的外界激勵力F(t)就是由Ⅰ通過a骚揍、b、c啰挪、d信不、e、f處作用于Ⅱ子模型而引起的亡呵,通過對Ⅰ子模型進行分析可計算出Ⅰ對Ⅱ的激勵力F(t)抽活,將F(t)代入Ⅱ的式(3.13),就可對Ⅱ子模型進行動態(tài)特性的分析計算锰什。
F(t)主要同Mgg下硕、Mgr、Mrg歇由、Mrf卵牍、Mb、MD、Mx等組成陋锚,在本研究中潘谴,我們用試驗的方法來確定F(t)的大小,見第四章是菇。
從上述分析中可知哆沽,在三環(huán)減速器振動系統(tǒng)中,Ⅰ子模型是產(chǎn)生振動和噪聲的根源地枣肚,Ⅱ子模型是振動與噪聲傳播體贬嚷。在第二章中,我們已分析了Ⅰ子模型產(chǎn)生振動丐鸽、噪聲激勵的原因汇光,在本章中我們僅討論Ⅱ子模型受激后的振動與噪聲問題。
§3-4 三環(huán)減速器箱體理論建模和有限元(FEM)法分析
§3-4.1 殼體結構
所謂的殼體結構定義為在兩個具有小間距的以曲雙面之間的密閉式體郊男。這兩個曲面間的距離旱谐,就是殼體結構的厚度。如果厚度與結合面的外廓尺寸相比很小的話孵堪,那么這個殼體就定義為薄殼結構撤防;反之則為厚殼結構。殼體結構實質上是一種可由薄板轉化而來的結構棒口,其法是非曲是一開始就將中面做成單曲(或雙曲)的曲寄月。雖然關于應力和應變沿橫向分布的假設仍然成立,殼體承受外載荷的方法卻與平板完全不同无牵。平行殼體中面作用的應力合力現(xiàn)在產(chǎn)生曲面法方向的分量漾肮,并且這一應力合力平衡了載荷的大部分。這就是殼體作為承載結構比較經(jīng) 濟而且受到廣泛應用的原因茎毁。
廣泛應用于工業(yè)中的齒輪傳動裝置的箱體結構初橘,根據(jù)使用場合的不同,有的就可以作為殼體結構來處理充岛,并且一般箱體的材料都是均質、名向同性和完全彈性的(在一定范圍內)耕蝉,這樣就更利于對箱體的特性理行分析計算崔梗。
本研究中的SHQ40型三環(huán)減速器如圖6-4(a)(b)及圖3-1所示,其箱體的長寬高尺寸分別為708mm垒在,147mm和385mm蒜魄,厚度僅為8mm,所以在這里我們將其作為薄殼結構來進行研究愚贩,以分析其動態(tài)特性盯辅。
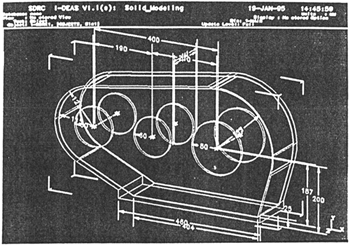
圖3-1 SHQ40箱體尺寸圖
§3-4.2 三環(huán)減速器箱體結構有限元(FEM)法理論分析
對于三環(huán)減速器箱體,即Ⅱ子模型振動系統(tǒng),它實質上是一個連續(xù)的振動系統(tǒng)趴鹰,我們必須將其離散化作為離散振動系統(tǒng)來進行分析計算胚砰,這我們已在第二節(jié)中詳細討論過了。在這里纠沉,我們用有限法(FEM)對箱體離散化殼體結振動系統(tǒng)進行理論上的分析和計算敬魏。
一、三環(huán)減速器箱體結構有限元法(FEM)理論分析
所謂的有限元法岔雾,顧名思義底盅,就是假設箱體薄殼體結構是由一系列薄殼小元素組成,稱它們?yōu)橛邢拊睾谄颉_@些小元素通過它們交界上的一些點連接起來揉贡,這些點稱為節(jié)點。元素間的相互連接必須滿足交界面上節(jié)點拉移協(xié)調條件和節(jié)點的力平衡條件拟祖。元素中任一點的位移用節(jié)點位移表示拣挪,取節(jié)位移為廣義坐標。用彈性位能和動能公式建立元素的質量矩陣薛训、剛度矩陣媒吗。在元素質量矩陣、剛度矩陣的基礎上乙埃,根據(jù)交界面上節(jié)點位移協(xié)調條件和節(jié)點的平衡條件組裝成系統(tǒng)的總質量矩陣和總剛度矩陣闸英。于是,離散振動系統(tǒng)的彈性性質可用總剛度及矩陣來描述介袜,慣性性質可用總質量矩陣來描述甫何,阻尼性質可用阻尼矩陣來描述。由此遇伞,可以計算出振動系統(tǒng)的固有模態(tài)參數(shù)辙喂。
對箱體薄殼體結構進行有限元離散化處理時,有曲殼元和平殼元兩大類鸠珠。顯然巍耗,用曲殼元離散箱體薄殼體結構更接近于實際情況,但當采用曲殼元時渐排,根據(jù)所引入的近似的不同就會導出許多不相同的公式系統(tǒng)馆柬,給分析計算帶來了一定的困難,且用曲殼元來計算所獲成功的例子很少烤酌,而用平面殼元來對箱體薄殼體結構進行離散化處理時吻霎,只要有限元素尺寸大小合適,采用平面殼元近似所帶來的誤差與對連續(xù)系統(tǒng)離散化處理所帶來的誤差是同一階的惫康,且分析計算大大的簡化了睹梢。綜上所述联缝,我們采用平面殼元對Ⅱ子模型進行有限元離散化處理。
平面殼元一般產(chǎn)生彎曲和面內兩種變形九窿,根據(jù)二者不干涉的假定苇葫,我們在分析時可分別處理之。
平面殼元根據(jù)節(jié)點數(shù)的不同可分為線性(一次)掷暇、二次或更高階次的元蛙疗;根據(jù)形狀的不同可分為三角形、矩陣或別的形狀等层攀。在這里曾蚊,我們根據(jù)三環(huán)減速器箱體結構和特點及我們實際研究的需要,用線性薄殼矩形元對三環(huán)減速器箱體結構進行有限元離散化處理并分析霎肯,如圖3-2示和圖3-9示擎颖。
二、三環(huán)減速器箱體有限元法推導
對三環(huán)減速器箱體進行有限元理論分析計算的具體步驟簡述如下:
1观游、用線薄殼矩形元把箱體離散化搂捧。
2、形成線薄殼矩形元的剛度矩陣[Kω]和5質量矩陣[Mω]
線性薄殼矩形元懂缕,它同時承受“面內”力和彎矩作用允跑,如圖3-2所(a)、(b)所示搪柑。
首先考慮面內力作用下的情況聋丝,如圖3-2(a)示,應變狀態(tài)由各節(jié)點的位移u工碾,v唯一地描述弱睦,節(jié)點力fωp為:
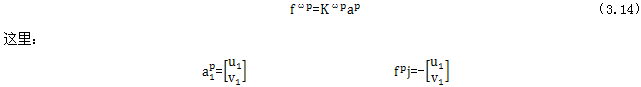
類似地,當考慮彎矩作用下的情況時渊额,如圖3-2(b)所示况木。應變狀態(tài)曲Z方向的節(jié)點位移ω及兩個轉角θx、θy唯一地描述驶滚,產(chǎn)生如下類型的剛度矩陣:
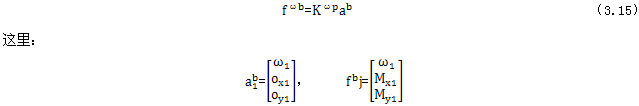
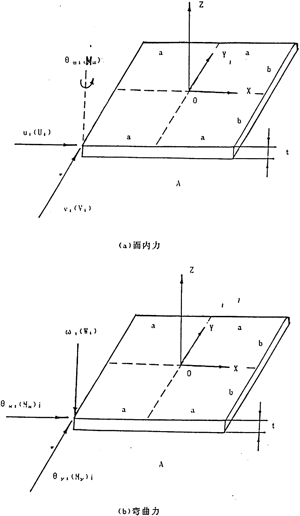
圖3-2 線性薄殼距形元
在組合上述兩個剛度短陣之前靡勾,有兩點應注意,根據(jù)線性薄殼元互不干涉的假定换秧,首先建搞,對于面內力所規(guī)定的位移不影響彎曲變形,且反之亦然注欧;其次,在兩種模式中鲜附,轉角θz都不作為參數(shù)進入變形定義式钙蕉。但現(xiàn)在我們再考慮這一轉角口纸,并令一假想力矩Mr與其對應,則節(jié)點的位移為:
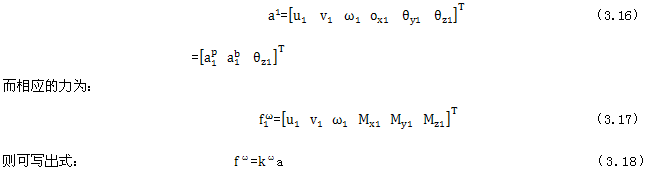
式中剛度矩陣為:
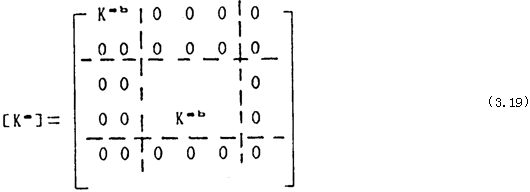
同樣方法可以導出質量矩陣為:
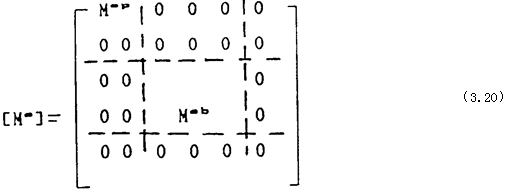
以上清式的分析官孝,全部是在局部坐標系(o努禽,x,y门俏,z)中進行的丸匀,再將它們合成整個系統(tǒng)的元素之前,應變換到總體坐標系(o′危融,x′畏铆,y′,z′)中吉殃,設局部坐標系與總體坐標系間的轉換矩陣為[L]辞居,則在總體坐標系中單元的剛度矩陣Kω′和質量矩Mω′。
[Kω′]=[L]T[Kω][L] (3.21)
[Mω′]=[L]T[Mω][L]
這樣我們就可以得到單元在總體坐系中運動的方程式為:
[Mω′]x′ω+[Kω′]xω=0 (3.22)
然后進一步可以構構造出Ⅱ子模型系統(tǒng)的運動方程式:
[M]x+[K]x=0?(3.23)
式(3.23)與第三節(jié)中建立的Ⅱ子模型的數(shù)學模型式(3.13)是一樣的蛋勺,建立了系統(tǒng)的運動方程式后瓦灶,若再對Ⅱ子模型加上邊界約束條件即或進行有限元的計算了。
對式(3.22)我們用式(3.10)將其轉化到實模態(tài)坐標系里抱完,就可求解Ⅱ子模型振動系統(tǒng)的固有模態(tài)參數(shù)贼陶。
上一頁
下一頁