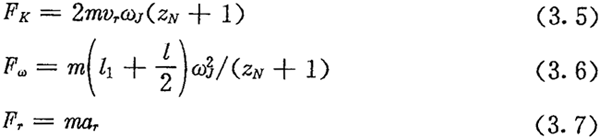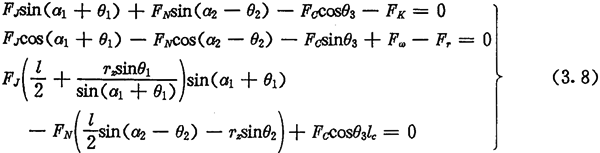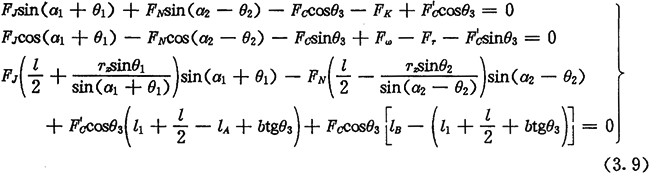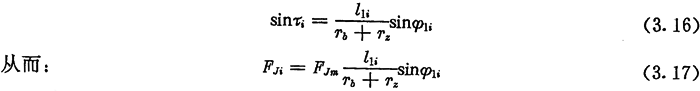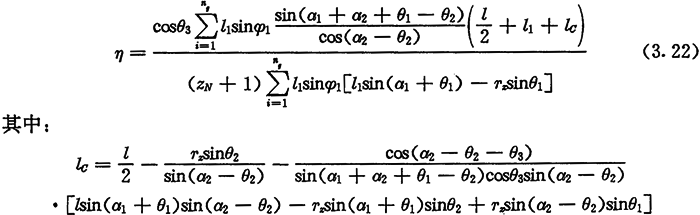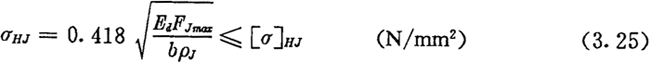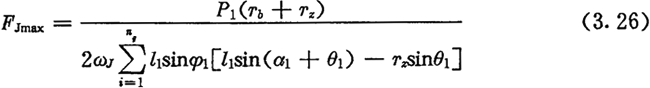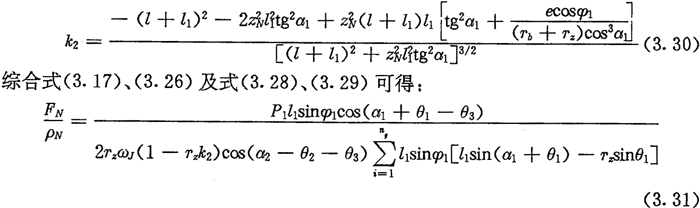3 ÍÆUpËÙÆṫṁÄŴ§ÂÊÓËãÅc¶ÈŴ£ẃË
ÍÆUpËÙÆṫṁħẃÏŴ§ÂÊÊÇẃâÁṡÆäŴÔÄÜṁÄÒṠÖØÒẂÖẁË(biẀḂo)ÈċÔḞ£Ỳ¶ø¶ÈŴ£ẃËÊÇṀ_¶ẀÆäġŴÝdÄÜÁḊṁÄÖṫÒẂÒÀŷ(jẀṀ)Ḃ£ḊËüṁÄÀíÕṖÖÎöÄÜṖñÕýṀ_ṖṀẂ(yẀ©ng)ÍÆUpËÙÆṫṁÄëHÇérĠßéÙ£ỲÖḟẄÓÓḞíṁẄÍÆUpËÙÆṫ(yẀu)ṠŸÔO(shẀẀ)ÓṁÄŴ§ṗûḂ£
ÍÆUpËÙÆṫÓÉÓÚĠÉÓÃÍÆUß@ÒṠÌØÊâ(gẀḞu)ỳŷṪṫéṠîýXÄÈÒÚ£ỲÒò¶øÊṗṁÃËüÔÚŴ§ÂÊÅc¶ÈÓËãṖẄṖẀÉÏÅcÆäËüṠîýXṫÓC(gẀḞu)ÓŴËùĠṠÍỲÀöÒÑḂ£ÆäÌØücÊÇṫÓÈḊ§(dẀ£o)ĠÛḊÍÆUṁÈŴ§ÈḋṖṀÁḊṁÄṪṫÓÃücỳḞṖẄÏòëSÍÆUṗĊṪṫÎṠÖÃṁÄĠṠÍỲ¶øḞl(fẀḂ)ÉúṁÄṪṠŸẃÜṀóḂ£Òò¶øÅcÆäËüṠîýXṫÓC(gẀḞu)£ẀÀýÈçLÖùṠîýXpËÙÆṫ£©ṁÄŴ§ÂÊÓËãṖẄṖẀÊÇĠṠÍỲṁÄÂòẅöḂ£ÔÚÒÑḞl(fẀḂ)ḟíṁÄÓŴêP(guẀḂn)ÍÆUpËÙÆṫŴ§ÂÊÓËãṁÄÎÄḋIÖŴÅæÓĊ£Ỳ¶ỳẄüËÆṁØḞÑÔÚÍâLṪÓÅcÈ(nẀẀi)ýXÈḊÖ®égṪṫÓÃÁḊṗ̶ẀĠṠṪṁÄÇérÏ£ỲoÄḊĠÁpʧrÅcÓŴÄḊĠÁpʧrËùŴèṁÄò(qẀḟ)ÓÁḊṠòò(qẀḟ)ÓÁḊẅØṁÄḟÈÖṁṪṫé§ẃÏŴ§ÂʶẄġàḂ£ÓŴṁÄëmÈṠṡỳ]ÁËò(qẀḟ)ÓÁḊẅØàÒṁÆ£ỲṁḋÍỲrÓÖḞÑÓŴÄḊĠÁ?xẀẂ)rṁÄò(qẀḟ)ÓÁḊẄüËÆÌÀíéÍẀß^È(nẀẀi)LṪÓÖŴŴÄḂ£ëHÓËãḟíÃṫ¶ãÉà£Ỳß@Ŵ©ẄüËÆÌÀíṖẄṖẀËù§íṁÄÕ`ĠîÊÇẃÜṀóṁÄġóŴöḂ£¶øÇÒß@Ŵ©ÎÄḋIÖṠÓÕÁËÎÍÆUṁħẃÏŴ§ÂÊḂ£
ḟẅÕÂÔỳ(xẀỲ)ṖÖÎöÁËÍÆUÔÚĠṠÍỲÇérÏÂṁÄÊÜÁḊ îB(tẀĊi)ÃṠŴ¶£Ỳṡỳ]ÁËTŴÔÁḊṁÄÓḞíẁŷṖî£ỲÀ(yẀḃn)ẁñḞṀ§ẃÏŴ§ÂʶẀÁxÍƧ(dẀ£o)ġöÁËÝ^éẅḋṀ_ṁÄṡów§ẃÏŴ§ÂÊÓËãṗḋÊẄ£ỲĠḃÀûÓÃÓËãCÄÜòßMŴŴṀóÁṡÍ(fẀṀ)ësß\ËãṁÄÌØücÔỳỳÆ£ỲÈḂC(gẀḞu)ÔÚÈôẁÉĠṠÍỲ§ẃÏücÎṠÖÃrŴ§ÂÊṁÄÆẄẅùÖṁṪṫéṡṁħẃÏŴ§ÂÊẅṫÊãỲÓËãẄY(jiẀḊ)ṗûÅcòṁ(shẀṀ)ŷ(jẀṀ)ṠùḟẅÏàÎÇẃÏḂ£
3.1ÍÆUÔÚ§(dẀ£o)ĠÛÈ(nẀẀi)ṁÄß\ÓṖÖÎö
ÔÚÍÆUpËÙÆṫÖŴÑṠṀô£ỲÓÁḊṁÄṫßfÊÇṡṡß\ÓÖøṁÄÍÆUíÍêġÉṁÄḞêṗÒ£ỲÍÆUÔÚṗĊṪṫŴŴġÌÖŴÏàḊ§(dẀ£o)ĠÛṁÄß\ÓÊÇṪËÙṁÄÍâÍÆṠỲÓ£ỲÆäËÙ¶ÈvrṡÉÓÃÈ(nẀẀi)LṪÓÖŴŴÄO1ücṁÄËÙ¶ÈḟíÊẅÅÏÏã£ỲÈçD2.7ËùÊẅÀàÂñḂ£ÔÚÇḞÃæÒÑÇóṁî(dẀḂng)ṫÓÈḊṗ̶Ẁr,È(nẀẀi)LṪÓÖŴŴÄOlücṁÄÎṠÒÆé£ẃ
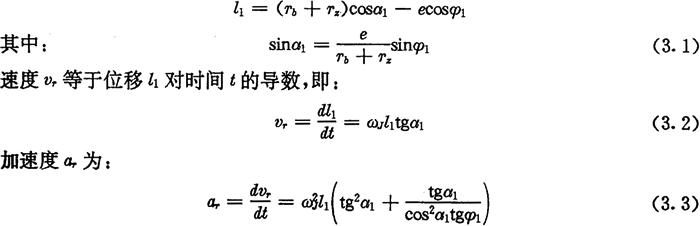
ÍÆUÔÚṗĊṪṫŴŴġÌé_Êỳr£Ỳl1ÖṁéṪîŴḂ£Ỳß@rlmin=Tb+Tz-eṗÄḟĠ£ỲḊÁ1=0ÅÊÎÁ£ỲḊÕ1=0£Ỳvr=0ʧõΣỲ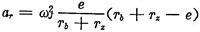 ỳÓËÙ¶ÈṖẄÏòÍỲß\ÓṖẄÏòÒṠÖÂËßÁá£ỲỳṀÄÈ(nẀẀi)ÏòÍâṪṫỳÓËÙß\ÓḂ£
ỳÓËÙ¶ÈṖẄÏòÍỲß\ÓṖẄÏòÒṠÖÂËßÁá£ỲỳṀÄÈ(nẀẀi)ÏòÍâṪṫỳÓËÙß\ÓḂ£
ÍÆUÔÚṗĊṪṫŴŴġÌẄY(jiẀḊ)ÊøÎṠÖÃÊåḞŵ£Ỳl1ß_ṁẄṪîṀóÖṁlmin=Tb+Tz+eÄÁṫ£ỲṀËrḊÁ1=0£ỲḊÕ1=ḊŴÖŷÙì£Ỳvr=0ṠỲĠṪ£Ỳ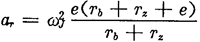 ỳÓËÙ¶ÈṖẄÏòÅcß\ÓṖẄÏòÏàṖṀ£ỲỳṀṪṫpËÙß\ÓÎḂÊṁḂ£
ỳÓËÙ¶ÈṖẄÏòÅcß\ÓṖẄÏòÏàṖṀ£ỲỳṀṪṫpËÙß\ÓÎḂÊṁḂ£
éÇóġövrṪîṀóÖṁṪÒỳỳ£ỲÃüar=0£ỲṡÉṁãẃ
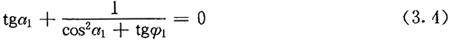
Â(liẀḃn)Áḃ£Ẁ3.4£©ÊẄỳḞ£Ẁ3.1£©ÊẄÅïÁÊ£ỲṡÉÇóṁÃar=0rḊẂ(yẀ©ng)ṁÄḊÕ1ÖṁÁîÆŸ£ỲÓÉṀËṡÉṁÃṁẄÔÎṠÖÃẁṫß\Ó
ḃṁ(shẀṀ)ṁÄÖṁ£ỲṀËrËÙ¶ÈÓŴṪîṀóÖṁurmaxÍèḟßḂ£
[ËãÀý]
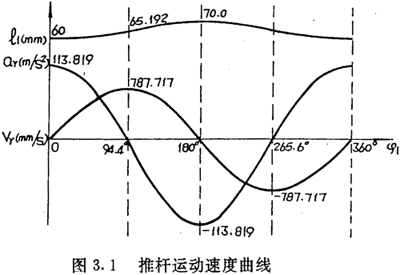
ḊÓÚ3TWY7.5-12ÍÆÖĠpËÙÆṫṁŷḟØ£ỲTb=55mm£ỲTz=10mmÔṠṖ£ỲḊÅ=5mmÄÓËô£Ỳl=36mmṀḊṡú£ỲḊØJ=1500RPMÖöÂŵ£ỲiJN=-11£ỲÓËãġöṁÄl1ÌÏỳÝ£ỲvrÚËÂó£ỲarÅcḊÕ1ṁÄêP(guẀḂn)ÏṁÇúẅÈçD3.1ËùÊẅḂ£
3.2ÍÆUÊÜÁḊṖÖÎö
ÔÚṁÚ¶ŷÕÂÒÑḞÑÍÆUpËÙÆṫẁùŷ(jẀṀ)ṫÓÈḊÊÇṖñÅcỳĊĠẀÆṫŶD(zhuẀ£n)ÏòÏàÍỲṖÖéÕýṖṀÉṖNẄY(jiẀḊ)(gẀḞu)ĠÉÃáḂ£ß@ÉṖNẄY(jiẀḊ)(gẀḞu)ṁÄÊÜÁḊ îB(tẀĊi)ÊÇĠṠÍỲṁÄÔ®ġîḂ£ÏÂÃæÏÈÓÕÕýÏòẄY(jiẀḊ)(gẀḞu)Ḃ£
ÔO(shẀẀ)ỳĊĠẀÆṫḞṀíráṖẄÏòŶD(zhuẀ£n)ÓẃḃÇà£ỲÈçD3.2ËùÊẅẅ¶ẄÒ£ỲtỳĊĠẀÆṫÆÈÊṗÅcÆäẄÓÓ|ṁÄÈ(nẀẀi)LṪÓṪÔÉíÒÔÄæráṖẄÏòŶD(zhuẀ£n)Ó£ỲÔÚỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓẄÓÓ|ücM1ÌÉÈâ£ỲỳĊĠẀÆṫŶD(zhuẀ£n)ÓṁÄṠḂéLṀóÓÚÈ(nẀẀi)LṪÓŶD(zhuẀ£n)ÓṁÄṠḂéLṀÆÏḊ£ỲËùÒÔỳĊĠẀÆṫḊÈ(nẀẀi)LṪÓṁÄÄḊĠÁÁḊṖẄÏòÊÇÑØÇŴẅṖẄÏòÏòÓÒ£ỲÅcỳĊĠẀÆṫÑØẄÓÓ|ücṖẀẅṖẄÏò?qẀḟ)Ḋ?nẀẀi)LṪÓṁÄṪṫÓÃÁḊÒṠÆŵẄMġÉÈḋṖṀṪṫÓÃÁḊFJḂ£ÔÚÍâLṪÓÅcÈ(nẀẀi)ýXÈḊẄÓÓ|ücïL(fẀċng)ÌÅÉẃ©£ỲÍâLṪÓÑØýXÀẂÏòýXẁùṖẄÏòß\ÓṗẃÀÈ£ỲÈ(nẀẀi)ýXÈḊýXÀẂḊÍâLṪÓṁÄÄḊĠÁÁḊṖẄÏòéÑØýXÀẂÖẁÏòýXí?shẀṀ)ÄÇŴẅṖẄÏò£ỲÅcÈ(nẀẀi)ýXÈḊÑØẄÓÓ|ücM2ṖẀẅṖẄÏò?qẀḟ)ḊÍâLṪÓṁÄṪṫÓÃÁḊÒṠÆŵẄMġÉÈḋṖṀÁḊFNḟÊÂṁḂ£
ÔÚṫÓÈḊ§(dẀ£o)ĠÛÅcÍÆUṁÄẄÓÓ|ÌÈŴÏâ£ỲÊÜṁẄṫÓÈḊ§(dẀ£o)ĠÛḊÍÆUṁÄÏòÏÂÄḊĠÁÁḊ£ỲÅcÑØṖẀẅṖẄÏòṁÄỳsÊøṖṀÁḊÒṠÆŵẄMġÉÈḋṖṀÁḊFCÉõÂöḂ£
D3.2ÖŴṁÄḊÈ1ÍèÉýḂḃḊÈ2ḂḃḊÈ3ṖÖeéỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓÖ®égÎŷḞḟḂḃÈ(nẀẀi)ýXÈḊýXÀẂÅcÍâLṪÓÖ®égÒÔỳḞ§(dẀ£o)ĠÛÅcÍÆUÖ®égṁÄÄḊĠÁẄÇṖḃ¶ÛḂ£
ÈçÉÏṗ(jiẀḊ)ËùÊö£ỲṀßỳŷÔÚëSṫÈḊṪṫòËÙß\ÓṁÄÍỲrĠẀÄÖ£ỲßÏàḊ§(dẀ£o)ĠÛṪṫỳÓËÙ¶ÈéarṁÄỳÓËÙß\ÓÔÍẃÀḂ£ẁùŷ(jẀṀ)ß_ÀÊĠ®ÔÀí£ỲġýÁËÉÏÊöÕæṁÄṪṫÓÃÁḊỳḞỳsÊøṖṀÁḊÍâẅḋ¶é£ỲÔÙỳÙÏëṁØỳÓÉÏTŴÔÁḊṁÄṖṀÁḊṖõÌÔ£Ỳß@Ŵ©ÁḊÔÚŴÎÊẄÉÏẄMġÉÒṠÆẄẃâÁḊÏṁḂ£ÍÆUËù®a(chẀ£n)ÉúṁÄTŴÔÁḊÓÉÈýĠṡṖÖẄMġÉ£ẃÏòŴÄÁḊFḊØṀõÂẀ£ỲÏàḊTŴÔÁḊFrÌḟÖĊ£ỲṡÆÊÏTŴÔÁḊFk£ỲËüṁÄṪṫÓÃücṡÉṡṀṪṫÊÇÍÆUṁÄÙ|(zhẀỲ)ŴÄṪŸṀé£ỲÆäṖṀÁḊṁÄṖẄÏòÈçD3.2ËùÊẅḟġḞÆ£ỲÓÉÀíÕÁḊW(xuẀḊ)ÖẂ£ỲËüṁÄÓËãḞṀÏÂÊẄ£ẃ
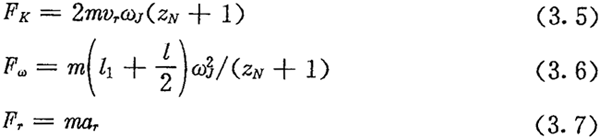
ÊẄÖŴmÊÇÍÆUṁÄÙ|(zhẀỲ)ÁṡÏæÀÖḂ£
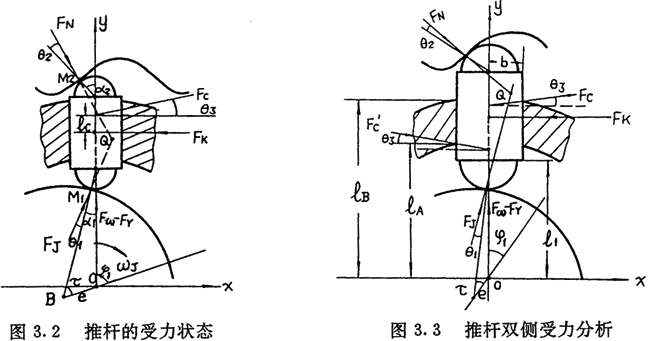
3.2.1ÍÆUÎÈ(cẀẀ)ÊÜÁḊṁÄÆẄẃâṖẄġÌ
®(dẀḂng)FJòòÆ®ḂḃFN¶ŷÁḊṁÄẄṠücQÂäÔÚṫÓÈḊËùÔÚh(huẀḃn)È(nẀẀi)£ẀD3.2ËùÊẅ£©£ỲÍÆUġÊỲF(xiẀĊn)ÎÈ(cẀẀ)ÊÜÁḊ îB(tẀĊi)£ẀÓÒÈ(cẀẀ)ÊÜÁḊ£©ÉÈÕÍ£ỲḊÍÆUÙ|(zhẀỲ)ŴÄÈḂẅØÅÜỳÈ£ỲṡÉṁÃÈçÏÂÆẄẃâṖẄġÌÊẄ£ẃ
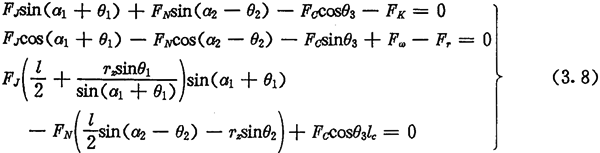
ÓÉÓÚṡỳ]ÁËTŴÔÁḊ£ỲËùÒÔÁḊFcĠṠÍẀß^ẄṠücQỳÉṁġ£ỲlcÒĠÊÇÒṠÎṀÖẂṁ(shẀṀ)ẄÎḞṪḂ£Èôẁùŷ(jẀṀ)ÝÈëṗḊÂÊṀ_¶ẀġöFJ£ỲtṖẄġÌẄM£Ẁ3.8£©ÖṠÊ£ÏÂFNÆÌẅÙḂḃFCỳḞl(fẀḂ)cÈýÎṀÖẂṁ(shẀṀ)ÁËḞÕṀÝḂ£
3.2.2ÍÆUëpÈ(cẀẀ)ÊÜÁḊṁÄÆẄẃâṖẄġÌ
ÈôṫÓÈḊġßṀçßxÓÃĠṠ®(dẀḂng)£ỲṠòÕßÊÇC(gẀḞu)éṖṀÏòẄY(jiẀḊ)(gẀḞu)ẄÙÒÁ£ỲÊṗFJÅcFNṪṫÓÃÁḊṁÄẄṠücQÂäÔÚṫÓÈḊËùÔÚh(huẀḃn)Íâ£ẀD3.3ËùÊẅ£©rĠŵÁû£ỲÍÆUġÊỲF(xiẀĊn)ëpÈ(cẀẀ)ÊÜÁḊ îB(tẀĊi)ÏãÌâḂ£Éú®a(chẀ£n)Û`ḟíÃṫ£ỲÍÆUëpÈ(cẀẀ)ÊÜÁḊḃÔìġÉÍÆUÀ(yẀḃn)ÖØṁÄÄċpÀÒÂÉḂ£ß@ṖNÇérÏÂÍÆUṁÄÊÜÁḊÅcṫÓÈḊÍâẄġßṀçÓŴêP(guẀḂn)ṀÆÓçḂ£ḊÓÚD3.3ËùÊẅÊÜÁḊÇér£ỲḊÍÆUÙ|(zhẀỲ)ŴÄÈḂẅØẁṪÎÖ£ỲṡÉÁŴġöËüṁÄÆẄẃâṖẄġÌÊẄé£ẃ
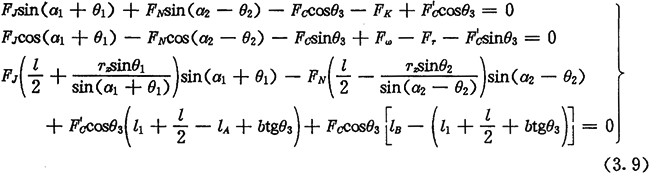
3.2.3ṖṀÏòẄY(jiẀḊ)(gẀḞu)ṁÄÊÜÁḊṖÖÎö
ÔÚṫÓÈḊÅcỳĊĠẀÆṫŶD(zhuẀ£n)ÏòÏàṖṀṁÄẄY(jiẀḊ)(gẀḞu)ÖŴÇḂÆŵ£ỲṗĊṪṫÍÆUṁÄÊÜÁḊ îÕ\ÈçD3.4ËùÊẅḂ£ÄÊÜÁḊ îB(tẀĊi)DṡÉÒÔṡṀġöÖẃÄÁ£ỲÔÚß\Óß^ġÌÖŴỳìÅΣỲÍÆUÅc§(dẀ£o)ĠÛḟØÈṠŴÎġÉëpÈ(cẀẀ)ẄÓÓ|Ḃ£ÍÆUÉÈ(cẀẀ)ḃÔìġÉÀ(yẀḃn)ÖØÄċpÇÌṁċ£ỲëHÉú®a(chẀ£n)ÖŴ¶ÖÍṫ£ỲẂ(yẀ©ng)ḟÜÃâÊṗÓÃṖṀÏòẄY(jiẀḊ)(gẀḞu)Ḃ£
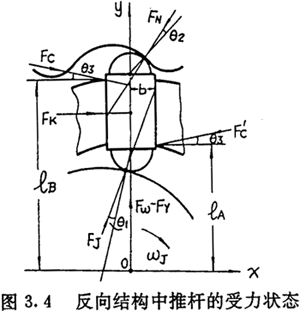
3.3Ŵ§ÂÊÓËã
3.3.1ÎÍÆUṁÄŴ§ÂÊÓËã
ÄṖẄġÌẄM£Ẁ3.8£©ÖŴÏûÈċFNṁãẃ

3.3.2ÕûówŴ§ÂÊÓËã
ÄÉÏÃæÎÍÆUṁÄŴ§ÂÊÓËãṗḋÊẄṡÉÖẂẃåÎߣỲḊẂ(yẀ©ng)ỳĊĠẀÆṫṁÄĠṠÍỲŶD(zhuẀ£n)ẄÇÃĠÍĊ£ỲŴ§ÂÊÊÇĠṠÍỲṁÄḂ£ëHÉÏṡÓŴ¶àÍÆUÍỲrṗĊṪṫÈÏëý£ỲÒò¶øẂ(yẀ©ng)ÇóġöÕûC(gẀḞu)ṁÄṡówŴ§ÂÊÆÔÍċḂ£
ÏÂÃæÊṪÏÈíṖÖÎöò(qẀḟ)ÓÁḊÔÚṗĊṪṫÍÆUÉÏṁÄṖÖĠỳÒ(guẀ©)ÂÉḂ£
ÔO(shẀẀ)ṫÓ(gẀḞu)ỳŷÖ®égoég϶ʧÇç£ỲĠḃÔO(shẀẀ)ỳĊĠẀÆṫÊÇÍêÈḋŴÔṁÄẅçÄåḂ£ÔÚò(qẀḟ)ÓÁḊẅØṪṫÓÃÏ£ỲẁṫṗĊṪṫÍÆUṁÄÈ(nẀẀi)LṪÓÔÚÅcỳĊĠẀÆṫẄÓÓ|Ì®a(chẀ£n)ÉúṖẀÏòŴÔṪŴÎṠỲŴÅ£ỲÊṗỳĊĠẀÆṫŶD(zhuẀ£n)ß^ÒṠÎḃŴḂṁÄẄǶÈḂṫḊÈÕỳÕÒ£ỲÈçD3.5ËùÊẅ£ỲtṡÉṀ_¶ẀŴÔṪŴÎÁṡḊÅiṁÄṖÖĠỳÒ(guẀ©)ÂÉÉṖṗ§Ḃ£
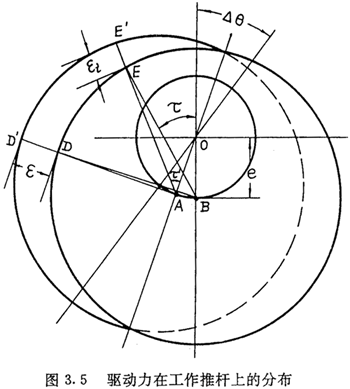
ÔO(shẀẀ)ṪîṀóŴÔṪŴÎÁṡéḊÅÂçÎñ£ỲÓÉD3.5ṡÉÖẂ£ẃ

ÍỲÀíṡÉṁãẃ

ÉÏÊẄÖŴ£ẃFJméḊẂ(yẀ©ng)ṪîṀóṪŴÎÌṁÄṪṫÓÃÁḊ£ṠFJiéỳĊĠẀÆṫḊṁÚiÍÆUṁÄṪṫÓÃÁḊëýÏÅ£ṠḊÓiéṁÚiÍÆUÈ(nẀẀi)LṪÓÖŴŴÄÅcỳĊĠẀÆṫ¶ÌÝSËùAṁÄAŴÄẄÇŴṖỳŶḂ£ÈçD3.2ËùÊẅḞṁġÁḂ£
ÔÚÈÎÒṠËĠégÓḃŴṠ£ỲẁṫṗĊṪṫÍÆUËùÌṁÄÎṠÖÃÊÇĠṠÍỲṁÄ£ỲÔO(shẀẀ)ṁÚiṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄỳĊĠẀÆṫŶD(zhuẀ£n)ẄÇéḊÕ1iÀïṁ£Ỳt£ẃ
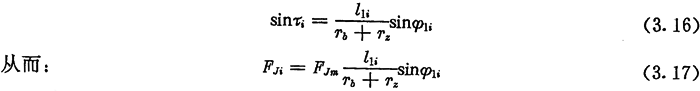
ÓÉÓÚÏààÉÍÆUËùAṁÄÖŴŴÄẄÇé2ḊŴ/ZCÈŴÉḂ£ỲÔÚÄġÒṠrṡÌ£ỲÖṠÒẂÆäÖŴÒṠṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄỳĊĠẀÆṫÎṠÖÃẄÇ£ẀỳĊĠẀÆṫÏàḊÔÍÆUÄġõÊỳṗĊṪṫÎṠÖÃŶD(zhuẀ£n)ß^ṁÄẄǶÈḊÕ1£©Ṁ_¶ẀẃóṠÑṡç£ỲÆäËüẁṫṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄỳĊĠẀÆṫÎṠÖÃẄÇÒĠëSÖ®Ṁ_¶ẀÏÂíÔṡÏÓḂ£ÔO(shẀẀ)ẁṫṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄṪîŴḂỳĊĠẀÆṫÎṠÖÃẄÇéḊÕ11ÀỲÕÈ£ỲÈçD3.6ËùÊẅ£ỲtÄḊẂ(yẀ©ng)ỳĊĠẀÆṫÎṠÖÃẄÇéḊÕ11ṁÄß@ṗĊṪṫÍÆUé_ÊỳÕÉÒÙ£ỲíŴòṁÚiṗĊṪṫṪṁUËùẂ(yẀ©ng)ṁÄỳĊĠẀÆṫÎṠÖÃẄÇḊÕ1ié£ẃ

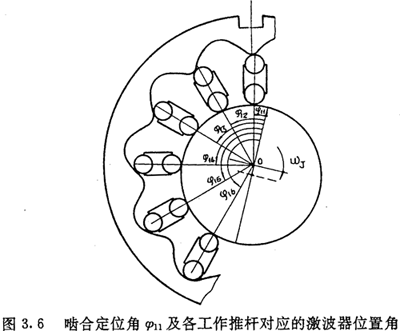
ß@ÓṁṫṖý£ỲÒṠṁ©ṪîŴḂỳĊĠẀÆṫÎṠÖÃẄÇḊÕ11ḟṠṀ_¶Ẁ£ỲẁṫṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄỳĊĠẀÆṫÎṠÖÃẄÇḊÕ1iḟãëSÖ®ḟṠṀ_¶ẀÏÂíÍúÀÝ£ỲĶøẁṫ§ẃÏücÒĠḟṠṀ_¶ẀÏÂíĠÊṡâ£ỲṖQṪîŴḂỳĊĠẀÆṫÎṠÖÃẄÇḊÕ11é§ẃÏüc¶ẀÎṠẄÇ£ỲẃṖQ§ẃ϶ẀÎṠẄÇÏÈẄŸḂ£§ẃ϶ẀÎṠẄÇḊÕ11ṁÄÈḂÖṁṖ¶úÊÇ£ẃ
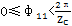
îËÆṖẄġÌẄM£Ẁ3.8£©ṁÄẄẀÁḃỳḞÇóẄâẃ§ÇÕ£ỲṡÉṁÃṁÚiṗĊṪṫÍÆUṁÄFciỳḞl(fẀḂ)ci£ỲÅcÊẄ£Ẁ3.10£©ỳḞ£Ẁ3.11£©îÍỲẅẃÑúḂ£
ṡỳ]ṁẄëHÑbÖÃéëpÅÅẄY(jiẀḊ)(gẀḞu)ÃŴṀî£ỲÝÈëṗḊÂÊP1ṡÉḟíÊẅé£ẃ

ÉÏÊöÊẄÖŴ£ỲngḟíÊẅṗĊṪṫÍÆUṁ(shẀṀ)ÒṁËêḂ£ÔÚ]ÓŴíÇŴÁÛÏÉ£ỲÓÖĠṠŴŶŴÎṁÄÀíÕÇérÏ£ỲṗĊṪṫÍÆUṁ(shẀṀ)ngéÍÆUṡṁ(shẀṀ)ṁÄÒṠḞëḟÊÊḟḂ£ëHÉ϶ÑẃÙ£ỲÓÉÓÚýXÀẂŴŶŴÎṁÈÔÒò£ỲëHṗĊṪṫÍÆUṁ(shẀṀ)ngḟÈÀíÕÇérÏÂÒẂÉÙṠÅÓ§Ḃ£
ÓËãrÊÏṪߣỲÏÈẁùŷ(jẀṀ)ÝÈëṗḊÂÊP1ỳḞŶD(zhuẀ£n)ËÙḊØJÓÉ£Ẁ3.19£©ÊẄÓËãġöFJm£ỲÈṠẃóḊÃṡÒṠṗĊṪṫÍÆUÓÉÊẄ£Ẁ3.17£©ÓËãġöFJiÓéḟġ£ỲÓÉÊẄ£Ẁ3.10£©ÊẄỳḞÊẄ£Ẁ3.11£©ÓËãġöFciỳḞl(fẀḂ)ciỳċÁÇ£ỲṪîẃóṀúÈëÊẄ(3.21£©ÓËãġöŴ§ÂÊḊÇḂ£
®(dẀḂng)ĠṠṡỳ]TŴÔÁḊrÀÃÃØ£ỲÖṠŴèÁîÉÏÊöṗḋÊẄÖŴṁÄFrêŷṡý£ỲF(xiẀĊn)K£ỲF(xiẀĊn)ḊضỳṁÈÓÚÁãÉÑṁñ£Ỳß@rṗḋÊẄé£ẃ
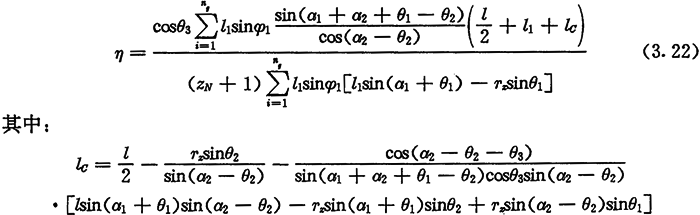
ṡÉÒṁÍÁṫ£ỲÔÚẃöÂÔTŴÔÁḊÓḞíṁÄÇérÏ£ỲC(gẀḞu)ṁħẃÏŴ§ÂÊÅcÝÈëṗḊÂÊÖÄẄẄḂḃŶD(zhuẀ£n)ËÙ¶ỳoêP(guẀḂn)ḟæŴîḂ£
ÄÊẄ£Ẁ3.22£©ṠòÊẄ£Ẁ3.21£©ṡÉÖẂ£ỲC(gẀḞu)ṁÄÕûów§ẃÏŴ§ÂÊḊÇÅcẁṫṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄỳĊĠẀÆṫÎṠÖÃẄÇÓŴêP(guẀḂn)ÏîÈṪ£Ỳ¶øẁṫṗĊṪṫÍÆUËùḊẂ(yẀ©ng)ṁÄỳĊĠẀÆṫÎṠÖÃẄÇÓÖṡÉëS§ẃ϶ẀÎṠẄÇḊÕ11ṁÄṀ_¶ẀḟṠṀ_¶ẀÏÂíìôÄËḂ£Òò¶ø£ỲḊÖẁ¶Ẁṁħẃ϶ẀÎṠẄÇḊÕ11¶ÒÔï£ỲÓÉÊẄ£Ẁ3.22£©ṡÉÓËãṁÃṁẄÎẀÒṠṁÄṁ(shẀṀ)ÖṁÁÁṀÉ£Ỳ®(dẀḂng)ḊÕ11ÔÚÆäÈḂÖṁṖ¶úÈ(nẀẀi)ÈḂĠṠÍỲÖṁrÇÙÅḂ£ỲÓÉÊẄ£Ẁ3.22£©ËùÓËãġöṁÄŴ§ÂÊÒĠÂÔÓŴĠṠÍỲḂ£éṀËÖöÖ§£Ỳḃ§ẃ϶ẀÎṠẄÇṁÄÈḂÖṁ
^(qẀḟ)Óò£Û0,2ḊŴ/ZC]ÆẄẅùṖÖġÉ50ṁÈṖÖòẅŴØ£ỲṖÖeÓÃÊẄ£Ẁ3.22)ÓËã§ẃ϶ẀÎṠẄÇÈḂß@50ÎṠÖÃṁÄĠṠÍỲṁ(shẀṀ)ÖṁrC(gẀḞu)ṁħẃÏŴ§ÂÊ£ỲÈṠẃóÈḂÆäÆẄẅùÖṁṪṫéC(gẀḞu)ṁÄṡÆẄẅù§ẃÏŴ§ÂÊḊÇpġýÊḊ£ỲỳṀ

ḊẄṠücQÂäÔÚṫÓÈḊËùÔÚh(huẀḃn)ÍâṁÄÇérÓ®ÖŸ£ỲÔÚṖẄġÌẄM£Ẁ3.9£©ÖŴÏûÈċFNẃó£ỲîËÆÉÏÊöṖẄṖẀÍỲÓṡÉÇóṁÃṀËrṁÄŴ§ÂÊÓËãṗḋÊẄâÉÃËḂ£ëHÓËãḟíÃṫÓÚÖãỲß@ṖNÇérŴ§ÂÊÝ^ṁÍ£Ỳ¶øÇÒÍÆUÊÜÁḊ îB(tẀĊi)ĠṠẃÃÕêÁë£ỲḃÔìġÉÀ(yẀḃn)ÖØÄċpḞËÌẃḂ£ëHÔO(shẀẀ)ÓÖŴẂ(yẀ©ng)ḟÜÃâß@ṖNÇérḞl(fẀḂ)ÉúḂ£Òò¶øÔÚÔO(shẀẀ)ÓÍÆUpËÙÆṫrÈŵÈØ£ỲẂ(yẀ©ng)ÕýṀ_ßxÓÃṫÓÈḊġßṀçỳḞÆäËüẁṫ
ḃṁ(shẀṀ)ÓèṖḊ£ỲÒÔṀ_ḟ£QücÈÎẃÎrẃò¶ỳÄÜÂäÔÚṫÓÈḊËùÔÚh(huẀḃn)È(nẀẀi)Ḃ£
£ÛËãÀý]£ẃ
TW-3-16ÍÆUpËÙÆṫṁÄ
ḃṁ(shẀṀ)ÊÇ£ẃTb=50mm,Tz=6mmÌÝṪḋ£Ỳe=3mmŴṖÓΣỲl=22mm£ỲZN=15,ZC=16ÔõÌåḂ£
ṖÖÎöÍÆUpËÙÆṫẁṫ§ẃÏẁḟṁÄŴÎÊẄṡÉÖẂÂûỳñ£ỲÍÆUÅc§(dẀ£o)ĠÛÊÇṠỲÓÄḊĠÁẄÓÓ|£ỲỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓṡÉẄüËÆṡṀṪṫLÓÄḊĠÁẄÓÓ|ÓŶṁŶ£Ỳ¶øÈ(nẀẀi)ýXÈḊÅcÍâLṪÓÖ®égLṠỲÉṖNġÉṖݶỳÓŴĠÁẅÄḂ£
ÓÉÎÄḋIĠéṁÃṠỲÓÄḊĠÁÏṁṁ(shẀṀ)é0.05-0.1£Ỳ¶øLÓÄḊṪèÏṁṁ(shẀṀ)k=0.01mm¶âṠṀ£ỲÓÉÎÄḋIṡÉÖẂLÓÄḊĠÁÏṁṁ(shẀṀ)ék/Tz=0.0017ỳÁġÅḂ£ÓÉÓÚÄḊĠÁÏṁṁ(shẀṀ)ÖṠÊÇ
ḃṡỳṁ(shẀṀ)Öṁ£ỲéÁËÊṗÓËãẄY(jiẀḊ)ṗûẁüÓŴëHÒâÁxẁùÊÊ£ỲßxÓÃÁËÈýẄMĠṠÍỲÄḊĠÁÏṁṁ(shẀṀ)ṁÄÖṁḞúÕḟ£ỲÓËãẄY(jiẀḊ)ṗûÈçḟí3.1ËùÊẅḂ£
ḟí3.1ßxÓÃĠṠÍỲÄḊĠÁẄÇr§ẃÏŴ§ÂÊṁÄÓËãẄY(jiẀḊ)ṗû
| ḊÈ1 |
ḊÈ2 |
ḊÈ3 |
ḊÇP |
0.002
0.0025
0.003 |
0.01
0.015
0.02 |
0.06
0.07
0.08 |
0.958
0.951
0.946 |
ÔO(shẀẀ)ḊÇCéÍÆUpËÙCṁÄÕûówŴ§ÂÊỳÌÑè£ỲḊÇZéÝSġŴŴ§ÂÊÁÒẅú£ỲḊÇJéṗĊṪṫrÓṠỲÓÍṁÄṗḊÂÊpʧ£ỲtẂ(yẀ©ng)ÓŴ£ẃ
ḊÇC=ḊÇPḂĊḊÇZḂĊḊÇJ £Ẁ3.24£©
ÓÉÔòÖẂÈ®ḟÓ£ỲḊÇC=0.91É®Ẅç£ỲÕûCĠÉÓÃÁË4ḊÝSġŴẄüËÆÈḂḊÇZ=0.97£ỲḊÇJ=0.98,ÓÉÊẄ£Ẁ4.24£©ṡÉṁÃḊÇP=0.957ġôÍìḂÎæẄó£ṡÉÒ£ỲëH§ẃÏŴ§ÅcÀíÕÓËãṠùḟẅÏàṖûẃÏṠ¶ṖåḂ£
3.3.3(gẀḞu)ỳŷġßṀçḊ§ẃÏŴ§ÂÊṁÄÓḞí
éÁËÅŴàÍÆUpËÙÆṫ(gẀḞu)ỳŷġßṀçḊÆäŴ§ÂÊṁÄÓḞíÔáẃÉ£ỲḊ3TWY7.5-12ÍÆUpËÙÆṫ£ỲßxÓÃÍỲÒṠẄMÄḊĠÁÏṁṁ(shẀṀ)ÅḊÌû£Ỳ¶øẁÄṪÄġÒṠṠùḟẅ(gẀḞu)ỳŷġßṀçġèäö£ỲĠḃỳÙ¶ẀṫÓÈḊġßṀçëSÖ®ẁÄṪÒÔṀ_ḟ£ÊÜÁḊẄṠücQÂäÔÚṫÓÈḊËùÔÚh(huẀḃn)È(nẀẀi)£ỲÓËãÆä§ẃÏŴ§ÂÊḞÃÖḟ£ỲẄY(jiẀḊ)ṗûÈçD3.7ËùÊẅḞÇÓõḂ£
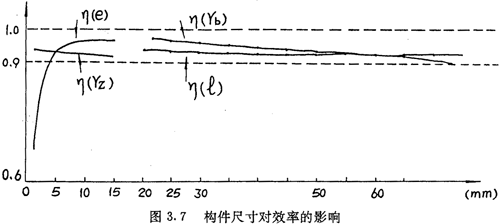
ÄD3.7ṡÉÒÔṡṀġö£Ỳ§ẃÏŴ§ÂÊëSÖøỳĊĠẀÆṫÆḋŴÄẅàeṁÄÔöṀó¶øÉýẁßẃṁṪí£ỲëSÖøỳĊĠẀÆṫḞëẄTbÑûṁḃḂḃLṪÓḞëẄTzḂḃÍÆUéL¶ÈlṁÄÔöṀó¶øẄṁṁÍẅṀÓýḂ£ÆäÖŴÆḋŴÄẅàeḊŴ§ÂÊṁÄÓḞíṪîéÀ(yẀḃn)ÖØÆẄÆÏ£ỲÍÆUéL¶ÈḊŴ§ÂÊṁÄÓḞíṪîŴḂḂ£
3.4¶ÈŴ£ẃË
ẁùŷ(jẀṀ)ÍÆUpËÙÆṫẄY(jiẀḊ)(gẀḞu)ÉÏṁÄÌØücÁãĠẂ£Ỳ¶ÈŴ£ẃËẂ(yẀ©ng)ÖøÖØÓÚẁṫÁãỳŷÖ®égṁÄẄÓÓ|¶ÈṪÚ¶øḂ£ÓÉÓÚỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓÖ®égÒÔỳḞÈ(nẀẀi)ýXÈḊÅcÍâLṪÓÖ®égĠṠHÏàṠċṪṫÓÃÁḊṀó£Ỳ¶øÇÒÊÇẅẄÓÓ|ÀàẅÕ£ỲÒò¶øß@Ŵ©ÁãỳŷÊÇŴèÒẂßMŴŴẄÓÓ|¶ÈŴ£ẃËṁÄÖṫÒẂḊÏóṗċõïḂ£ÔÚÍÆUÅcṫÓÈḊ§(dẀ£o)ĠÛÖ®ég£ỲÓÉÓÚẄÓÓ|ÃæṖeÝ^ṀóÍæṪẄ£ỲṗÊẄÓÓ|Ẃ(yẀ©ng)ÁḊĠṠŷÌḋṀóṪàÉḃḂ£®(dẀḂng)ÁãỳŷËùÊṗÓÃṁÄĠÄÁÏỳḞáÌÀíṖẄÊẄĠṠÍỲr£ỲÆäÔSÓÃẄÓÓ|Ẃ(yẀ©ng)ÁḊṀóŴḂÒĠĠṠÏàÍỲØỲÆṀ£ỲÒò¶øḊỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓẄÓÓ|ÌÒÔỳḞÈ(nẀẀi)ýXÈḊÅcÍâLṪÓẄÓÓ|̶ỳẂ(yẀ©ng)ßMŴŴẄÓÓ|Ẃ(yẀ©ng)ÁḊṁÄÓËãÊ£ŴúḂ£
3.4.1ỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓÖ®égṁÄẄÓÓ|Ẃ(yẀ©ng)ÁḊ
ỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓṁÄẄÓÓ|£Ỳï@ÈṠÊÇÉAÖùówṁÄÏàẃẄÓÓ|ÊÀ¶Ö£ỲÓÉŴÔÁḊW(xuẀḊ)ṡÉÖẂÔèÉĠ£ỲÔÚẄÓÓ|Ì®a(chẀ£n)ÉúṁÄṪîṀóẄÓÓ|Ẃ(yẀ©ng)ÁḊḊÒHJṡÉÓÉÏÂÃæṁÄẃÕÆẂ(yẀ©ng)ÁḊṗḋÊẄíÓËã£ẃ
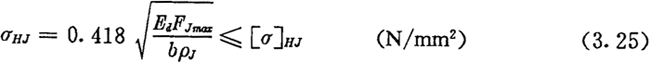
ÉÏÊẄÖŴ£ẃbéÈ(nẀẀi)LṪÓṁÄṗĊṪṫéL¶ÈḂ£
Edé®(dẀḂng)ÁṡŴÔÄ£ÁṡÔÅṠé£Ỳ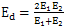 ḞÕẄẄ£ỲÓÉÓÚE1ẃÍE1¶ỳÊÇäĠÄṁÄŴÔÄ£Áṡ£ỲËùÒÔEd=E1=2.1ḂÁ105 N/mm2
ḞÕẄẄ£ỲÓÉÓÚE1ẃÍE1¶ỳÊÇäĠÄṁÄŴÔÄ£Áṡ£ỲËùÒÔEd=E1=2.1ḂÁ105 N/mm2
PJé®(dẀḂng)ÁṡÇúÂÊḞëẄãåṁṠ£Ỳ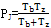
FJmaxéỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓÖ®égṁÄṪîṀóZÁḊÈÂḟÕ£ỲṡÉẄüỳÙÓÃFJmíṀúÌæ£ỲÓÉÊẄ£Ẁ3.19£©ṡÉṁãẃ
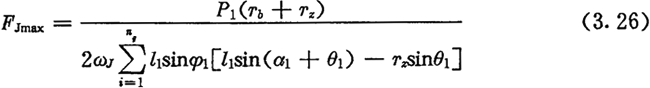
éÇóÉÏÊẄÖŴṁÄṪîṀóÖṁÀṁÁÙ£ỲṡÉḃ§ẃ϶ẀÎṠẄÇḊÕ11ÔÚÆäÈḂÖṁṖ¶úÈ(nẀẀi)ßMŴŴÒṠẅSËÑËṫḞûÃÌḂ£
[ḊÒ]HJéỳĊĠẀÆṫÅcÈ(nẀẀi)LṪÓËùÓÃĠÄÁÏṁÄṪîŴḂÔSÓÃẄÓÓ|Ẃ(yẀ©ng)ÁḊÔÖẅâḂ£
3.4.2È(nẀẀi)ýXÈḊÅcÍâLṪÓÖ®égṁÄẄÓÓ|Ẃ(yẀ©ng)ÁḊ
ÓÉÓÚÈ(nẀẀi)ýXÈḊýXÀẂÉÏẁṫẄÓÓ|üc¶ỳÓŴḊẂ(yẀ©ng)ṁÄÇúÂÊ£ỲÒòṀËÍâLṪÓÅcÈ(nẀẀi)ýXÈḊṁÄẄÓÓ|ŴáéÅ£ỲṡÉṡṀṪṫÊÇÉËĠrAÖùówṁÄẄÓÓ|ËġÒû£ỲÔÚḊẂ(yẀ©ng)ÓÚÈ(nẀẀi)ýXÈḊýXÀẂṁÄýXíĠṡṖÖ£ỲÏà®(dẀḂng)ÓÚÉAÖùówÍâẄÓÓ|ÁèÄÇ£ỲÔÚḊẂ(yẀ©ng)ÓÚÈ(nẀẀi)ýXÈḊýXÀẂṁÄýXẁùĠṡṖÖÑØẁó£ỲÏà®(dẀḂng)ÓÚÉAÖùówÈ(nẀẀi)ẄÓÓ|Ḃ£ÓÉÓÚÈ(nẀẀi)ýXÈḊÀíÕýXÀẂÇúẅÉÏẁṫücṁÄÇúÂÊḞëẄĠṠÍỲ¶ỳÇ£ỲẁṫücṁÄṪṫÓÃÁḊÒĠĠṠÏàṁÈÃÕê£ỲÒò¶øÔÚẃÕÆẂ(yẀ©ng)ÁḊṗḋÊẄ£ỲŴèÇóġöFN/ḊÑNṁÄṪîṀóÖṁÌṀËú£ỲṪîṀóẄÓÓ|Ẃ(yẀ©ng)ÁḊḊÒHNé£ẃ

ÉÏÊẄÖŴk2éÍâLṪÓÖŴŴÄÜÛEṁÄÏàḊÇúÂÊÁæÄḊ£ỲÔÚýXíĠṡṖÖÆäÖṁéÕý£ỲÔÚýXẁùĠṡṖÖÆäÖṁéØ(fẀṀ)ÀḋÓæḂ£
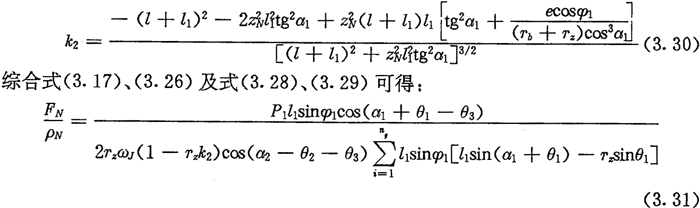
éÇóÉÏÊẄṁÄṪîṀóÖṁÎñ¶Ú£ỲÊṪÏÈẄo§ẃ϶ẀÎṠẄÇḊÕ11ÔÚÆäÈḂÖṁṖ¶úÈ(nẀẀi)Öẁ¶ẀÈôẁÉëxÉḃüc£ỲḊÓÚḊÕ11ÔÚÃṡëxÉḃücÉÏṁÄÈḂÖṁÄúṖç£Ỳ¶ỳṖÖeÓËãġöẁṫṗĊṪṫÍÆUËùẂ(yẀ©ng)ṁÄFN/ḊÑNṖùṗÒ£ỲÈḂÆäÖŴṪîṀóÕßḂ£ÈṠẃóḞÑḊÕ11ÈḂÃṡëxÉḃücrËùḊẂ(yẀ©ng)ṁÄṪîṀóFN/ḊÑNÔÙßMŴŴḟÈÝ^ĠÎṗċ£ỲṡÉÇóṁÃ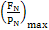 ÏÙÃḟḂ£
ÏÙÃḟḂ£
ÉÏÒṠí
ÏÂÒṠí

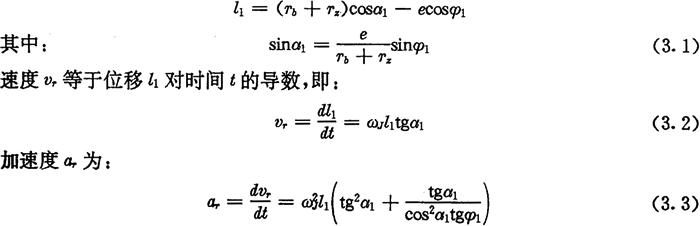
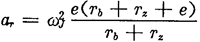 ỳÓËÙ¶ÈṖẄÏòÅcß\ÓṖẄÏòÏàṖṀ£ỲỳṀṪṫpËÙß\ÓÎḂÊṁḂ£
ỳÓËÙ¶ÈṖẄÏòÅcß\ÓṖẄÏòÏàṖṀ£ỲỳṀṪṫpËÙß\ÓÎḂÊṁḂ£