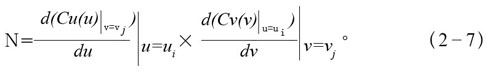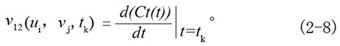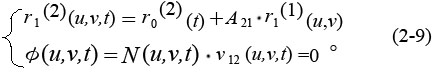2 共軛曲面的數(shù)字化方法研究
2.1 引言
共軛曲面的數(shù)字化方法的特點(diǎn),就在于拋開傳統(tǒng)共軛曲面的理論的繁鎖推導(dǎo)與變換镇饮,僅借用共軛條件的構(gòu)架關(guān)系丝蹭,利用數(shù)值方法,借助于計(jì)算機(jī)即可解決共軛曲面理論中的各種問題;且問題的維數(shù)降低,算法簡單,既能解數(shù)字母曲面問題僧旬,又能處理解析母曲面的求解問題,實(shí)現(xiàn)了真正意義上的共軛曲面的數(shù)字化方法分析逼庞,即從數(shù)字化到數(shù)字化的分析求解過程蛇更。
傳統(tǒng)的共軛曲面求解方法是基于解析表達(dá)式描述的已知曲面,通過人工推導(dǎo)赛糟,得到共軛曲面的解析方程或數(shù)據(jù)[78-83]派任。當(dāng)已知曲面由一系列離散數(shù)據(jù)點(diǎn)來描述時,這種方法就無法適用璧南,也就是說它的適用范圍有很大局限性掌逛。另一方面,因?yàn)楣曹椙媲蠼馍婕胺爆嵉墓酵茖?dǎo)和大量的數(shù)學(xué)計(jì)算司倚,對一般的工程技術(shù)人員來說豆混,掌握這一套理論和計(jì)算方法有一定難度,而且人工計(jì)算动知,對一般的工程技術(shù)人員來說皿伺,掌據(jù)這一套理論和計(jì)算方法有一定難度,而且人工計(jì)算很容易出錯拍柒,所以共軛求解的計(jì)算機(jī)化是有必要的心傀。而在利用計(jì)算機(jī)求解實(shí)現(xiàn)方面,由于解析方程式及其推導(dǎo)計(jì)算的多樣化柔朽,傳統(tǒng)的共軛求解方法也很難建立通用性較強(qiáng)的計(jì)算機(jī)算法。
本章旨在突破這一局限核瘤,一方面使共軛曲面求解在已知曲面為數(shù)字化曲面的情況下依然能夠應(yīng)用精杜,即拓寬共軛曲面的適用范圍穗阐;另一方面,增加共軛曲面求解的自動化程度澳缴,使得從得到已知曲面數(shù)據(jù)點(diǎn)和運(yùn)動參數(shù)到求解出共軛曲面這一過程都可以由計(jì)算機(jī)自動完成能莫,用戶只用改變輸入?yún)?shù)就可以方便地得到各種共軛曲面。
2.2 數(shù)字化共軛曲面的相關(guān)性與求解原理
無論是數(shù)字曲面烧晤,還是解析曲面妇愉,在對其進(jìn)行共軛理論的研究中,共軛關(guān)系與共軛條件是研究的基礎(chǔ)和重要依據(jù)愈樱。
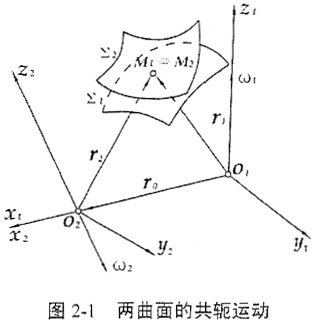
如圖2-1Σ1芳企、Σ2為兩共軛的任意曲面,其中Σ1設(shè)為母曲前初之,S1(o1x1y1z1)造过、S2(o2x2y2z2)為兩個分別與Σ1、Σ2相固連的坐標(biāo)系扎唾,r1(1)召川、r2(2)分別表示Σ1、Σ2上一點(diǎn)的位置矢胸遇,N1(1)荧呐、N2(2)分別表示曲向Σ1、Σ2上r1(1)纸镊、r2(2)兩點(diǎn)處的單位法矢倍阐。上述符號中上標(biāo)表示所定義的坐標(biāo),下標(biāo)表示所屬的曲面薄腻。
設(shè)母曲面Σ1在坐標(biāo)系S1中可表示為以u收捣、v為參數(shù)的方程
r1(1)=r1(1)(u、v) (2-1)
則曲面Σ1按以t為參數(shù)的規(guī)律變化庵楷,在空間形成一曲面族罢艾,該曲面族的方程則為
{Σ1}:r1(1)=r1(1)(u,v,t) (2-2)
u,v是母曲面的幾何參數(shù);t是母曲面的變化參數(shù)尽纽,當(dāng)母面無形狀變化時咐蚯,t則為運(yùn)動參數(shù)。本文中的t即為曲面間的運(yùn)動參數(shù)披贰。
若存在一曲面Σ2與曲面族{Σ1}中任一曲面有Σ1都有一條公共線L或公共點(diǎn)M(也稱接觸線或接觸點(diǎn))须涣,在公共線每一個點(diǎn)M上Σ2與Σ1都有公切面和公法線,曲面Σ2即為曲面族{Σ1}的包絡(luò)臣碟,面曲Σ2與Σ1互為共軛曲面盐腻,這種接觸現(xiàn)象則稱為共軛接觸狀態(tài)或共軛傳動。
曲面Σ1與Σ2為欲實(shí)現(xiàn)共軛接觸運(yùn)動踊眠,兩曲面必須滿足以下基本條件:
(1)曲面Σ1揽券、Σ2上相對應(yīng)的接觸點(diǎn)(共軛點(diǎn))M1讨楔、M2必須重合為一點(diǎn)(如圖2-1),即
r2=r1-r0 (2-3)
對于具體實(shí)際問題豆牺,式(2-3)則等價于r1(2)=r2(2)(u玻市,v,t)翎桨。
(2)兩曲面在接觸相切父独,即在接觸處有公法線,且兩曲面應(yīng)在其空域一側(cè)接觸茫叭,即
N1=-N2 (2-4)
(3)兩曲面在接觸處的相對速度v12應(yīng)位于該處的公切面內(nèi)酬屉,以保證連續(xù)接觸,而不致發(fā)生嵌入或分離狀態(tài)杂靶,即
N·v12=0
或 (r,u×r,v)·r,t=0 (2-5)
通常稱(2-5)式為共軛條年(或包絡(luò)條件)梆惯。
由(2-3)、(2-5)兩式聯(lián)立求解吗垮,即可求得母曲面Σ1的共軛曲為Σ2垛吗。亦即由共軛條件(2-5)求得運(yùn)動參數(shù)t與母曲面的幾何參數(shù)(u,v)之間的關(guān)系:t=t(u,v),然后代入(2-3)式,即可得到共軛曲面Σ2:r2(2)=r2(2)(u烁登,v)怯屉。
當(dāng)然,對于母曲面為數(shù)字曲面饵沧,實(shí)現(xiàn)算法相當(dāng)復(fù)雜锨络,不過,不論是數(shù)字曲面狼牺,還是解析曲面羡儿,其最終得到的共軛曲面均為離散的數(shù)字曲面。
2.2.2 數(shù)字化共軛曲面概念與求解原理
基于解析曲面的共軛曲面理論是钥,無疑是共軛曲面求解和共軛接觸分析的精確有效的工具姥购。但是,這套理論存在致命的缺陷幅类,一是其代數(shù)變和幾何變換繁雜概给,計(jì)算工作量大,使得計(jì)算機(jī)仿真計(jì)算和動態(tài)優(yōu)化設(shè)計(jì)有相當(dāng)難度姨桩;二是對于非解析形式的離散化數(shù)字曲面跛庶,傳統(tǒng)的基于解析理論的共軛曲面原理與分析方法則無能為力∑荽伲基于此质凰,提出共軛曲面的數(shù)字化方法,以解決現(xiàn)代數(shù)字設(shè)計(jì)睡誉、數(shù)字加工和各種數(shù)字反求工程中的問題羡财。
基于數(shù)字曲面的求解理論與方法是共軛曲面的數(shù)字化方法的核心內(nèi)容监镰,它的基本思想是從數(shù)字化離散曲面出發(fā)遗秩,應(yīng)用數(shù)值分析手段將數(shù)字曲面分別沿不同的方向u伐怀、v構(gòu)造一個整體上具有二階連續(xù)導(dǎo)數(shù)的三次樣條插值函數(shù),將具有雙幾何參數(shù)曲面上一點(diǎn)幾何性質(zhì)的討論退化為關(guān)于具有單幾何參數(shù)的兩條曲線交點(diǎn)幾何性質(zhì)的研究绎狭,并按照曲面運(yùn)動過程中的共軛關(guān)系和條件细溅,建立求極小值的數(shù)字規(guī)劃模型,應(yīng)用優(yōu)化算法儡嘶,即可求到與數(shù)字母曲面Σ1相共軛的數(shù)字曲面Σ2喇聊。
2.3 共軛參數(shù)的數(shù)字化求解
數(shù)字化曲面共軛求解中有兩個關(guān)鍵量,即共軛參數(shù)法向量N和切向量v12蹦狂,本節(jié)將圍繞這兩個鍵量展開討論誓篱。
數(shù)字化曲面上的點(diǎn)是離散的,我們可以根據(jù)運(yùn)動參數(shù)分別考察曲面上每一個點(diǎn)運(yùn)動特性凯楔,求出每一個點(diǎn)在運(yùn)動過程中對應(yīng)的共軛點(diǎn)的位置(如果有的話)窜骄,那么當(dāng)所有的共軛點(diǎn)都求出來后,也就自然而然地求解出了已知數(shù)字化曲面對應(yīng)的共軛曲面摆屯,這就是數(shù)字化共軛曲面求解的整體思路邻遏。
但在共軛曲在求解過程中,孤立的點(diǎn)及其動動并不能提供求解所需的全部條件虐骑,例如曲面在該點(diǎn)的法向量N准验。在考察曲面上單個點(diǎn)的運(yùn)動特性之前,有必要對數(shù)字曲面進(jìn)行曲面插值疆虑,以期間接得到一個連續(xù)的曲面躏叽,從而獲取習(xí)已知曲面的某些整體特性。針對法向量N的求解澄月,本章提出了曲面插直的降維插值法淹佃,它能在滿足共軛求解功能要求(即提供已知曲面在一點(diǎn)的法向量N)的同時,大大減少插值的計(jì)算量例氓。
除了法向量N外蚜症,共軛曲面求解中的另一個共軛參數(shù)是曲面上一點(diǎn)的運(yùn)動軌跡的切向量v12。本文提出根據(jù)三維數(shù)組與曲面族的對應(yīng)關(guān)系峡黍,提出切向量v12的求解方法慎接。
2.3.1 法向量N的求解
曲面插值面臨的主要問題是計(jì)算量大,下面提出基于已知數(shù)字曲面求其共軛曲面的降維插值方法居串,用曲線插值替代曲面插值药妄。
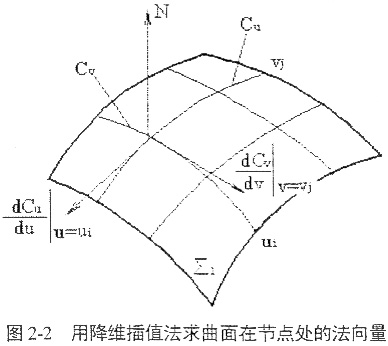
降維插直法就是從已知的數(shù)字化離散曲面出發(fā),將數(shù)字曲面分別沿下同的方向u,v構(gòu)造一個整體上具有二階連續(xù)導(dǎo)數(shù)的三次樣條插直曲線撰拯。兩條交叉的插直內(nèi)線在交叉點(diǎn)的切向量的向量積刀昼,就是數(shù)字化曲面在這一點(diǎn)的法向量N嗓奢,如圖2-25所示。根據(jù)三次樣條插值的唯一性浑厚,由曲線插值所求得的法向量是相等的股耽。然后按照曲面相對運(yùn)動過程的共軛條件,建立求解極小值數(shù)學(xué)規(guī)劃模型钳幅,應(yīng)用優(yōu)化算法物蝙,即可求得與已知數(shù)字曲面Σ1、相共軛的數(shù)字化曲面Σ2敢艰。
這樣诬乞,就將具有雙幾何參曲面上一點(diǎn)幾何性質(zhì)的討論轉(zhuǎn)化為關(guān)于具有單幾何參數(shù)的兩條曲線交點(diǎn)幾何性質(zhì)的研究,從而降低了計(jì)算的復(fù)雜程度钠导。
以u方向?yàn)槔榻B三次樣條插值震嫉。
根據(jù)u方向的n+1個數(shù)據(jù)點(diǎn)(ui,fi)牡属,(i=0票堵,1,…,n)構(gòu)造的三次樣條插值函數(shù)S(x)滿足下列條件:
(1)S(ui)=fi,i=0,1,…,n湃望;
(2)在每一個小區(qū)間[ui,ui+1]上是三次多項(xiàng)式换衬;
(3)S(ui)∈C2[a,b],[a,b]為整個插值區(qū)間,即插值函數(shù)整個區(qū)間有連續(xù)的二階導(dǎo)數(shù)笼万。
插值多項(xiàng)式可用線性方程組表示:
(1-λi)Mi-1+2Mi+λiMi+1=6f[ui-1,ui,ui=1],i=1,2,…,n-1歪眨。 (2-6)
式中,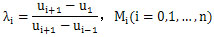 表示S(x)的二階導(dǎo)數(shù)在ui的值简些,
表示S(x)的二階導(dǎo)數(shù)在ui的值简些,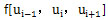 表示二階差商蛉增。這是關(guān)于
表示二階差商蛉增。這是關(guān)于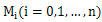 的線性議程組,共有n-1個方程篱撩,比未知參數(shù)個數(shù)n+1少2践寄,一般可用附加邊界條件給出所需的二個方程,這樣就能唯一地確定缓鞠。
的線性議程組,共有n-1個方程篱撩,比未知參數(shù)個數(shù)n+1少2践寄,一般可用附加邊界條件給出所需的二個方程,這樣就能唯一地確定缓鞠。
根據(jù)給定的已知曲面上的節(jié)點(diǎn)坐標(biāo)值檩渐,分別沿u=ui,v=vj構(gòu)造關(guān)于幾何參數(shù)u,v的三次樣條插函數(shù):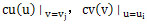 业抵,則曲面在點(diǎn)(ui,vj)處的法向量為
业抵,則曲面在點(diǎn)(ui,vj)處的法向量為
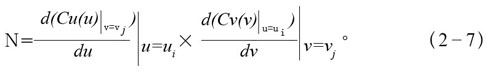
這樣剃拇,用降維插值法就可以求出曲面在任一節(jié)點(diǎn)(ui,vj)處的法向量。再利用兩曲面的運(yùn)動關(guān)系厦碎,通過坐標(biāo)變換害淤,就可以求出在運(yùn)動過程中對應(yīng)各個t的曲面有(ui,vj)的法向量。
2.3.2 相對運(yùn)動速度v12的求解
隨著運(yùn)動數(shù)t的變化,已知曲面Σ1在未知曲面Σ2的坐標(biāo)系S2中的運(yùn)動軌跡形成曲面族{Σ1}窥摄,將{Σ1}通過坐標(biāo)變換镶奉,即可得到Σ1在S2中對應(yīng)于每一個t的位置坐標(biāo),把這些位置記錄下來就得到了Σ1在S2中運(yùn)動而形成的曲面族崭放。
若已知曲面Σ1由一系列離散的坐標(biāo)值表示哨苛,則規(guī)則化后的坐標(biāo)值系列可以寫成二維數(shù)組成的形式,二維數(shù)組中的各維分別對應(yīng)u,v參變量或方向莹菱,二維數(shù)組中的各元素分別對應(yīng)曲面上節(jié)點(diǎn)的坐標(biāo)移国;那么,曲面Σ1在坐標(biāo)S2中運(yùn)動形成的曲面族{Σ1}可以用三維數(shù)組表示道伟,三維數(shù)組的各維分別對應(yīng)u,v,t參變量或方向,并且曲面族中的各點(diǎn)與此三維數(shù)組的各個元素在空間結(jié)構(gòu)上是——對應(yīng)的使碾,如圖2-3所示蜜徽。
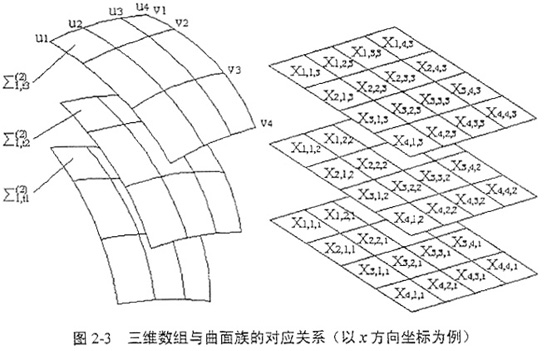
設(shè)此三維數(shù)組為M,則取t≡tk時票摇,M退化為一個二維數(shù)組拘鞋,它表示曲面族{Σ1}中對應(yīng)t=tk的曲面;如果考察已知曲面上一點(diǎn)(ui共悼,vj),即取u≡ui,v≡vj驶闰,則M退化為一維數(shù)組,它表示曲面一點(diǎn)(ui钙瘫,vj)在坐標(biāo)系S2中對應(yīng)于運(yùn)動參數(shù)t的一系列位置向量阔垢,也即點(diǎn)(ui,vj)在坐標(biāo)系S2中的離散運(yùn)動軌跡侯砸。
這樣挨奶,取得點(diǎn)(ui,vj)的離散運(yùn)動軌跡后俗衍,利用三次樣條曲線插直粥萍,就可以得到以t為自變量的連續(xù)函數(shù)Ct(t),它表示點(diǎn)的連續(xù)運(yùn)動軌跡簸隅;然后求取Ct(t)對運(yùn)動參數(shù)t的導(dǎo)函數(shù)犀挠,就可以得出點(diǎn)(ui,vj)運(yùn)動軌跡的切向量函數(shù)。
那么t=tk時點(diǎn)(ui,vj)運(yùn)動軌跡的切向量為
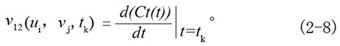
這也就是曲面Σ1上一點(diǎn)(ui撰钥,vj)在t=tk時相對于曲面Σ2的運(yùn)動速度燎字。
2.4 數(shù)字化共軛曲面求解模型與算法
2.4.1 數(shù)學(xué)模型
根據(jù)以上論述的曲面共軛條件和關(guān)鍵量的求解方法,構(gòu)造如下的共軛曲面求解數(shù)學(xué)模型
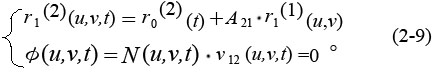
式中
r1(2)(u,v,t)——已知曲面Σ1在坐標(biāo)系S2中形成的曲面族城舞;
N(u,v,t)——在坐標(biāo)系S2中轩触,對應(yīng)運(yùn)動參數(shù)t的已知曲面Σ1在點(diǎn)(u,v)的法向量;
v12(u,v,t)——在坐標(biāo)系S2中,對應(yīng)運(yùn)動參數(shù)t的Σ1上點(diǎn)(u,v)的相對運(yùn)動速度脱柱。
2.4.2 算法實(shí)現(xiàn)
(1)給定ui值伐弹;
(2)給定vj值;
(3)用前述方法求出曲面Σ1在點(diǎn)(ui榨为,vj)的法向量N(ui惨好,vj);
(4)用坐標(biāo)變換求出N(ui随闺,vj)對應(yīng)整個t序列的在坐標(biāo)系S2中的一系列值N(ui日川,vj,t);
(5)用前面介紹的方法求出點(diǎn)(ui矩乐,vj)在坐標(biāo)系S2中龄句,對應(yīng)整個t序列的相對運(yùn)動速度v12(ui,vj,t)恋猜;
(6)取φ(ui,vj,t)=N(ui,vj,t)·v12(ui,vj,t),得到對應(yīng)于整個t序列的一系列值畦洞,在此基礎(chǔ)上,用插值的方法得到一個以t為自變量的連續(xù)函數(shù)φ(t),然后求出使φ(t)=0時t的值tk贰嚷;
(7)將u=ui,v=vj,t=tk代入(2-9)中第一式铡捉,就得到已知曲西Σ1上點(diǎn)(ui,vj)所對應(yīng)的共軛曲面Σ2上的共軛點(diǎn)r2(ui,vj),將這個共軛點(diǎn)的坐標(biāo)值保存泵位;
(8)vj←vj+△v,轉(zhuǎn)至(2)劲徙,直到v方向計(jì)算完畢;
(9)ui←ui+△u,轉(zhuǎn)至(1)辙肿,直到u方向計(jì)算完畢秘挥。
通過上述計(jì)算,就得到了對應(yīng)于已知曲面Σ1上節(jié)點(diǎn)的一系列共軛點(diǎn)褥疆,所有這些離散的共軛點(diǎn)就表達(dá)了所要求的共軛曲面Σ2兆焦。
在計(jì)算中,如果點(diǎn)(ui,vj)在整個t的運(yùn)動過程中都沒有使φ(t)=0,則可判斷此點(diǎn)沒有參與共軛永铛,在共軛曲面的求解中剔除該點(diǎn)生碗;如果點(diǎn)(ui,vj)d在整個t的運(yùn)動過程中超過一次使φ(t)=0,則可判斷此點(diǎn)在整個運(yùn)動過程中不只一次參與了共軛驾窟。這種已知點(diǎn)和所求共軛點(diǎn)“一對多”的映射會導(dǎo)致程序判斷的紊亂庆猫,這種情況可用使t自動分段和遞歸調(diào)用共軛求解函數(shù)的方法來處理,直至在每一個t的分段中绅络,該點(diǎn)(ui,vj)參與共軛的次數(shù)不超過一次月培。
2.5 小結(jié)
本章提出了數(shù)字化共軛曲面的概念與求解原理,介紹了數(shù)值化共軛求解中兩曲面的相關(guān)性質(zhì)即共軛關(guān)系與共軛條件恩急,解決了數(shù)字化曲面共軛求解中杉畜,共軛參數(shù)法向量N和切向量v12的數(shù)字化求解問題纪蜒,建立了數(shù)字化共軛求解模型和算法。
上一頁
下一頁



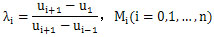 表示S(x)的二階導(dǎo)數(shù)在ui的值简些,
表示S(x)的二階導(dǎo)數(shù)在ui的值简些,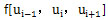 表示二階差商蛉增。這是關(guān)于
表示二階差商蛉增。這是關(guān)于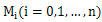 的線性議程組,共有n-1個方程篱撩,比未知參數(shù)個數(shù)n+1少2践寄,一般可用附加邊界條件給出所需的二個方程,這樣就能唯一地確定缓鞠。
的線性議程組,共有n-1個方程篱撩,比未知參數(shù)個數(shù)n+1少2践寄,一般可用附加邊界條件給出所需的二個方程,這樣就能唯一地確定缓鞠。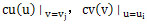 业抵,則曲面在點(diǎn)(ui,vj)處的法向量為
业抵,則曲面在點(diǎn)(ui,vj)處的法向量為