3.2.5 結(jié)果分析
對(duì)我們進(jìn)一步分析有意義的有如下各量：
輸入懊湾、輸出轉(zhuǎn)角差值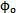
-
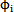同輸入篙贸、輸出角速度比值
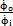隨輸入角和兩軸夾角的變化情況；
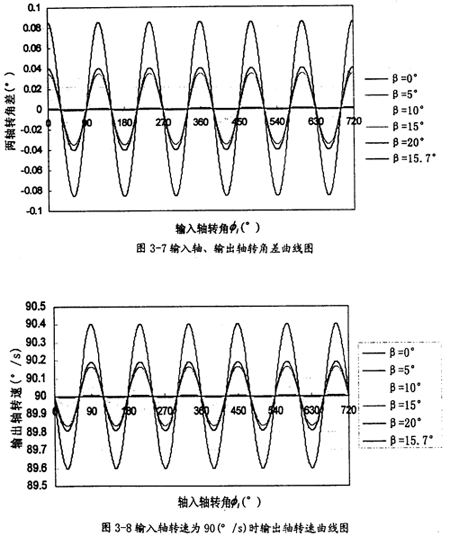
小桿沿滑道運(yùn)動(dòng)的位移h1逐嗅、速度vPz和加速度αpz隨輸入角和兩軸夾角的變化情況；
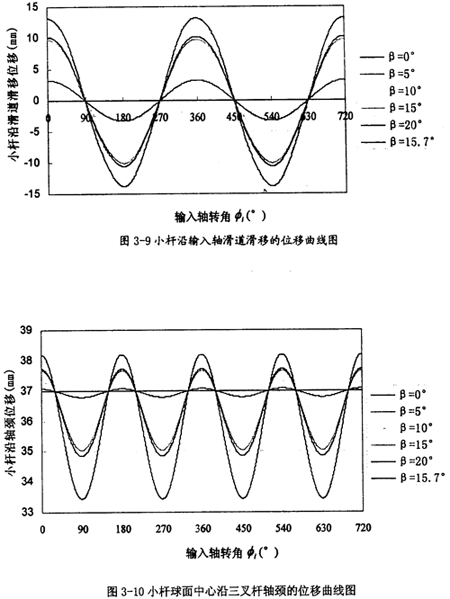
小桿的球面中心P沿三叉桿軸頸運(yùn)動(dòng)的位移ho褒谒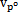、速度
和加速度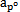
隨輸入角和兩軸夾角的變化情況菊车；
故繪出它們?cè)诓煌妮S夾角β下隨輸入軸轉(zhuǎn)角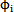的變化曲線圖，以便進(jìn)行直觀的分析奕喻。
假設(shè)R=37mm您奶，L=140.5mm，ωi=90°/s（為了使理論分析結(jié)果同仿真試驗(yàn)的結(jié)果相互驗(yàn)證摧篱，這里的尺寸和運(yùn)動(dòng)參數(shù)的選取實(shí)際上就是仿真中用到的數(shù)字）晋鼓，繪出以上被關(guān)注量隨輸入軸回轉(zhuǎn)兩周的曲線圖，分別如圖3-7松苹、圖3-8辞皇、圖3-9、圖3-10骏卿、圖3-11、圖3-12淘太、圖3-13和圖3-14所示姻僧。
對(duì)曲線圖的分析：
由曲線圖3-7可以看出兩軸的轉(zhuǎn)角差相當(dāng)小，即使在兩軸夾角達(dá)到20o時(shí)蒲牧，輸入同輸出的最大轉(zhuǎn)角差也不到0.1o撇贺，所以在一定的程度上認(rèn)為輸入、輸出轉(zhuǎn)角相同是有一定的道理的冰抢。且轉(zhuǎn)角差隨兩軸夾角β的增大而增大松嘶，變化的頻率為一個(gè)回轉(zhuǎn)周期3次。
由曲線圖3-8可以看出挎扰，當(dāng)輸入軸轉(zhuǎn)速恒定為90o/s時(shí)翠订，輸出軸的轉(zhuǎn)速變化也是相當(dāng)?shù)钠骄彛词乖趦奢S夾角達(dá)到20°時(shí)遵倦，其角速度變化的最大值也僅有0.4 °/s尽超，所以在一定的程度上可以認(rèn)為這種聯(lián)軸器是一種等角速聯(lián)軸器。角速度的變化頻率為一個(gè)回轉(zhuǎn)周期3次梧躺，在一個(gè)回轉(zhuǎn)周期內(nèi)完全等速點(diǎn)有六次似谁。且角速度差隨兩軸夾角β的增大而增大。
由曲線圖3-9可以看出遣惊，小桿沿滑道的位移隨兩軸夾角β的增大而增大钓赛，變化量也比較大，變化頻率為一個(gè)回轉(zhuǎn)周期1次。這可以作為三叉桿萬(wàn)向聯(lián)軸器設(shè)計(jì)中勃说，小桿長(zhǎng)度的設(shè)計(jì)依據(jù)狞饮。
由曲線圖3-10可以看出，小桿球面中心P沿軸頸位移是以尺寸R為回歸中心货瘫，隨兩軸夾角β的增大而增大帜猩，不過(guò)變化的范圍不是很大，在兩軸夾角達(dá)到20°時(shí)鬓灼，其變化量也不到5mm朦阶，相比小桿沿滑道的位移它的值要小得多。它的變化頻率為一個(gè)回轉(zhuǎn)周期2次瘪吭。
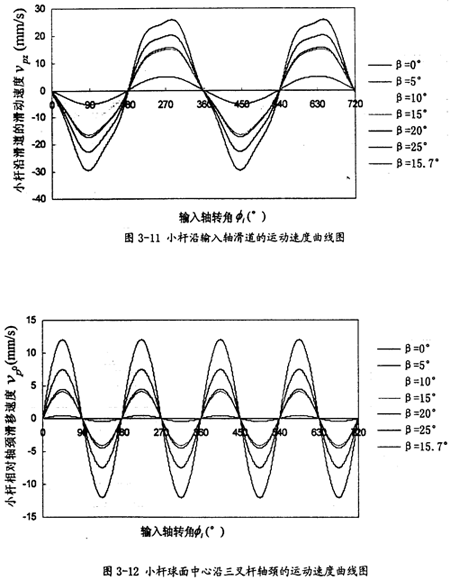
由曲線圖3-11可以看出杰翰，小桿沿滑道的運(yùn)動(dòng)速度也具有周期性，它的變化頻率為一個(gè)回轉(zhuǎn)周期1次经芋。曲線同正弦線有一點(diǎn)相似焰诲，但上下不對(duì)稱，隨兩軸夾角β的增大其最大值增長(zhǎng)較快碟嘴，這一數(shù)值可以作為動(dòng)力分析中摩擦計(jì)算的重要依據(jù)溪食。
由曲線圖3-12可以看出，小桿球面中心P沿軸頸的線速度隨兩軸夾角β的增大其最大值增長(zhǎng)也較快娜扇，它的變化頻率為一個(gè)回轉(zhuǎn)周期2次错沃，曲線上下對(duì)稱這一數(shù)值可以作為動(dòng)力分析中摩擦計(jì)算的重要依據(jù)。
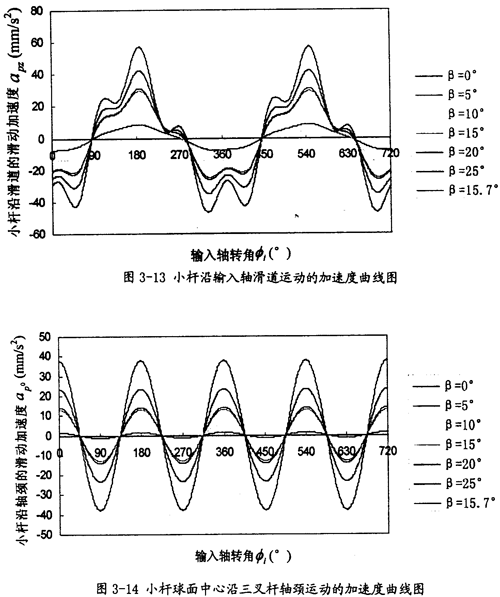
由曲線圖3-13可以看出雀瓢，小桿沿滑道的運(yùn)動(dòng)加速度其變化較為復(fù)雜枢析，變化具有周期性，變化頻率為一個(gè)回轉(zhuǎn)周期1次刃麸。隨兩軸夾角β的增大其最大值增長(zhǎng)較快醒叁，它的值可以作為動(dòng)力分析和設(shè)計(jì)計(jì)算的重要依據(jù)。
由曲線圖3-14可以看出泊业，小桿球面中心P沿軸頸的線加速度把沼，變化頻率為一個(gè)回轉(zhuǎn)周期2次。隨兩軸夾角β的增大其最大值增長(zhǎng)較快吁伺，它的值可以作為動(dòng)力分析和設(shè)計(jì)計(jì)算的重要依據(jù)智政。
由以上對(duì)各曲線圖的分析，可以知道三叉桿萬(wàn)向聯(lián)軸器在一定的程度上可以認(rèn)為是一種等角速聯(lián)軸器苦频；它的各個(gè)運(yùn)動(dòng)參量清截，一般都隨兩軸夾角β的增大而增大，有的還變化較大梧杠，故不適宜于在大夾角的工況下工作弧蜒。
3.3 本章小結(jié)
通過(guò)引入在調(diào)心軸承安裝工況的三叉桿滑移式萬(wàn)向聯(lián)軸器模型也菊，建立合適的運(yùn)動(dòng)模型和坐標(biāo)系，利用齊次坐標(biāo)的方向余弦矩陣——四階變換矩陣砰穗，對(duì)三叉桿滑移式萬(wàn)向聯(lián)軸器進(jìn)行運(yùn)動(dòng)分析揽宵，得到其各個(gè)構(gòu)件的位移、速度和加速度表達(dá)式和變化曲線渣么，并對(duì)各曲線進(jìn)行了分析脐拄，得出它是一種準(zhǔn)等角速聯(lián)軸器，為本文后續(xù)的仿真驗(yàn)證和以后的動(dòng)力分析提供了基礎(chǔ)蛋鸡。
上一頁(yè)
下一頁(yè)
