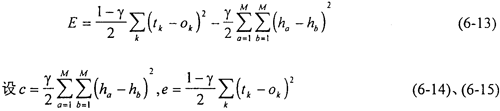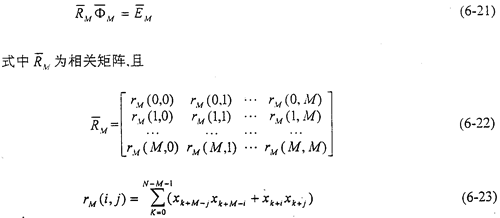6.2 基于MBP算法的設(shè)備故障智能診斷方法
普通BP訓(xùn)練算法在它的訓(xùn)練過程存在著不確定性除了上節(jié)提出的一些因素外儡首，還有一個重要的原因赎瞎，就是它的誤差函數(shù)不盡合理庸飘。它的誤差函數(shù)決定了靠近網(wǎng)絡(luò)輸出端的權(quán)在訓(xùn)練一開始調(diào)整較大肋演，而遠離輸出端的權(quán)在訓(xùn)練過程中調(diào)整始終較小，從而把網(wǎng)絡(luò)訓(xùn)練速度降低，甚至把網(wǎng)絡(luò)引入訓(xùn)練不收斂的地步。本節(jié)針對這種情況袖扛，采用一種新誤差函數(shù)，保證不管遠離還是靠近網(wǎng)絡(luò)輸出端的權(quán)在訓(xùn)練時同步調(diào)整十籍，提高了網(wǎng)絡(luò)訓(xùn)練速度和網(wǎng)絡(luò)收斂性蛆封，基于新的誤差函數(shù)的算法稱為MBP算法。算法如下：
誤差函數(shù)：
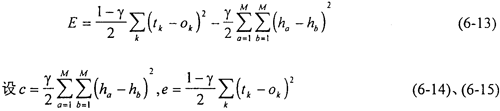
式中γ為隱層與輸入層權(quán)值參與因子勾栗，ha和hb分別為隱層的輸出惨篱。
6.2.1 誤差的反向傳播過程
1）對于輸出層與隱層之間有如下的權(quán)值調(diào)整公式
式中α和η的解釋同上節(jié)。對于小型網(wǎng)絡(luò)幌侧，γ可取較大的值令掠，一般為0.004～0.016，對于大的網(wǎng)格宽缎，γ應(yīng)取較小的值睹蜈，一般為0.00001～0.00022讶粹。
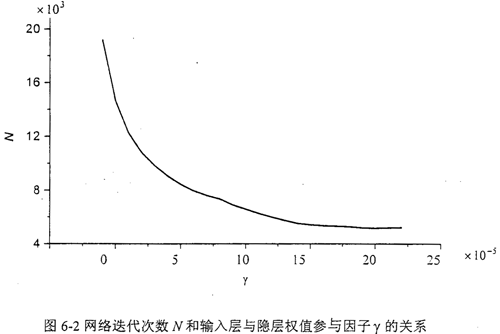
以表6-1標(biāo)準(zhǔn)訓(xùn)練樣本為例着雪，采用MBP法，網(wǎng)絡(luò)有較好的收斂性贩仇，訓(xùn)練速度有較大的提高瞎励，見圖6-2。圖中切役，當(dāng)γ=0時蒜肥，MBP法即為普通的BP算法。
6.2.2 算例
由于減速機故障樣式的多樣性蕉妇，故它的故障標(biāo)準(zhǔn)模式樣本的建立是比較困難的碟堵，需進行大量的試驗研究和實際設(shè)備故障診斷的總結(jié)和歸納。表6-5是在參考其它學(xué)者研究成果的基礎(chǔ)上腹忽，總結(jié)設(shè)備具體工作情況得出的減速機的故障標(biāo)準(zhǔn)模式樣本来累，表6-6為減速機標(biāo)準(zhǔn)訓(xùn)練樣本的訓(xùn)練結(jié)果（網(wǎng)絡(luò)規(guī)模為：輸入層節(jié)點數(shù)為：9個；一個隱層節(jié)點數(shù)為：40個窘奏；輸出層節(jié)點數(shù)為9個嘹锁；誤差精度為10-5葫录，網(wǎng)絡(luò)迭代次數(shù)為5217次）。圖6-3為某一有故障的軋鋼減速機的時域信號领猾，圖6-4為頻域信號米同。對圖6-4的頻域信號進行歸一化處理，可得待識別的故障樣本摔竿，用訓(xùn)練好的網(wǎng)絡(luò)對該樣本進行識別面粮。表6-7為該減速機故障樣本的識別結(jié)果。fa一軸頻继低，f0一軸承外圈故障特征頻率但金，fi一軸承內(nèi)圈故障特征頻率，fb一軸承滾動體故障特征頻率郁季，fmeh一齒輪嚙合頻率冷溃。
表6-5 減速機的故障標(biāo)準(zhǔn)模式樣本
| 故障類型 |
故障特征頻率及重要度 |
理想
輸出 |
| fa |
2fa |
3～4fa |
f0
2f0 |
f1
2f1 |
fb
2fb |
 |
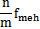fmeh |
2.3
fmeh |
| 軸 |
軸不平衡或彎曲 |
1.000 |
0.50 |
0.050 |
0.000 |
0.000 |
0.000 |
0.000 |
0.050 |
0.050 |
10000000
0 |
| 軸線不對中 |
0.800 |
1.000 |
0.080 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
01000000
0 |
| 軸生裂紋 |
1.000 |
0.800 |
0.600 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
00100000
0 |
軸
承 |
外滾道損傷類 |
0.000 |
0.000 |
0.000 |
1.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
00010000
0 |
| 內(nèi)滾道損傷類 |
0.000 |
0.000 |
0.000 |
0.000 |
1.000 |
0.000 |
0.000 |
0.000 |
0.000 |
00001000
0 |
| 滾動體損傷類 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1.000 |
0.000 |
0.000 |
0.000 |
00000100
0 |
齒
輪 |
全面點蝕或完全磨損 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
1.000 |
0.400 |
0.400 |
00000010
0 |
| 局部齒面損傷 |
0.400 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.600 |
0.600 |
00000001
0 |
| 兩齒輪軸不平行 |
0.700 |
0.400 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.600 |
0.600 |
00000000
1 |
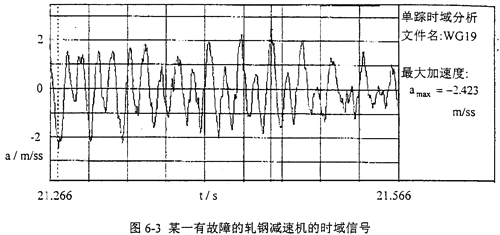
表6-6 標(biāo)準(zhǔn)訓(xùn)練樣本的訓(xùn)練結(jié)果
故障
樣本 |
軸不平衡或彎曲 |
軸線不對中 |
軸生
裂紋 |
外滾道損傷類 |
外滾道損傷類 |
滾動體損傷類 |
全面點蝕或完全磨損 |
局部齒面損傷 |
兩齒輪軸不平行 |
軸不平衡
或彎曲 |
0.9906 |
0.0000 |
0.0070 |
0.0024 |
0.0028 |
0.0031 |
0.0012 |
0.0026 |
0.0000 |
軸線
不對中 |
0.0003 |
0.9904 |
0.0085 |
0.0004 |
0.0031 |
0.0010 |
0.0013 |
0.0005 |
0.0008 |
| 軸生裂紋 |
0.0071 |
0.0081 |
0.9894 |
0.0042 |
0.0004 |
0.0014 |
0.0006 |
0.0000 |
0.0000 |
外滾道
損傷類 |
0.0015 |
0.0002 |
0.0008 |
0.9926 |
0.0034 |
0.0036 |
0.0028 |
0.0025 |
0.0000 |
外滾道
損傷類 |
0.0029 |
0.0035 |
0.0000 |
0.0031 |
0.9930 |
0.0036 |
0.0030 |
0.0018 |
0.0000 |
滾動體
損傷類 |
0.0022 |
0.0006 |
0.0000 |
0.0026 |
0.0030 |
0.9933 |
0.0027 |
0.0022 |
0.0000 |
| 全面點蝕或完全磨損 |
0.0007 |
0.0008 |
0.0000 |
0.0026 |
0.0032 |
0.0026 |
0.9929 |
0.0033 |
0.0000 |
局部齒
面損傷 |
0.0056 |
0.0000 |
0.0000 |
0.0039 |
0.0025 |
0.0023 |
0.0042> |
0.9886 |
0.0133 |
兩齒輪軸
不平行 |
0.0002 |
0.0048 |
0.0001 |
0.0007 |
0.0004 |
0.0007 |
0.0034 |
0.0105 |
0.9845 |
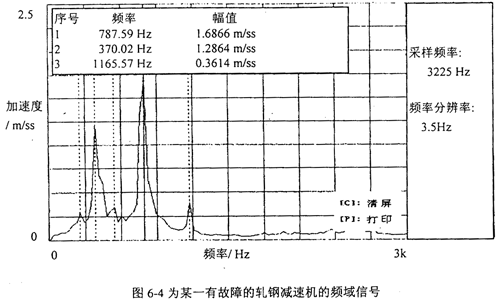
表6-7 該減速機故障樣本的識別結(jié)果
故障
類型 |
軸不平衡
或彎曲 |
軸線不
對中 |
軸生
裂紋 |
外滾道
損傷 |
內(nèi)滾道
損傷 |
滾動體
損傷 |
齒面點蝕或
完全磨損 |
局部齒
面損傷 |
齒輪軸
不平行 |
故障
程度 |
0.017 |
0.002 |
0.000 |
0.002 |
0.017 |
0.003 |
0.987 |
0.000 |
0.000 |
表6-7 識別結(jié)果與實際診斷結(jié)果一致
6.3 基于AR（M）模型的平穩(wěn)時序故障振動趨勢分析
通過對所記錄的故障振動數(shù)據(jù)序列的均值μx和方差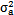
的檢驗，可判別出該振動數(shù)據(jù)序列是平穩(wěn)時間序列還是非平穩(wěn)時間序列弹双，從而為故障振動趨勢分析研究的建模提供了準(zhǔn)備碰素。對平穩(wěn)時間充列可采用較簡單的AR（M）模型建模和振動故障趨勢分析；對非平穩(wěn)時間序列可采用較實用的GM（1战辨，1）模型及AR（M）組合模型建模和振動故障趨勢分析媒邀，也可采用預(yù)報精度較高的神經(jīng)網(wǎng)絡(luò)組合預(yù)報模型，此內(nèi)容見6.5節(jié)和6.6節(jié)莱火。
6.3.1 AR（M）模型的建模
模型的建模包括以下過程：
1）數(shù)據(jù)的采集滴推；
2）數(shù)據(jù)的預(yù)處理：包括提取趨勢項、零化處理及標(biāo)準(zhǔn)化處理驻碟；
3）AR（M）模型的參數(shù)估計
對于AR（M）模型仪从，時間序列xt可表示為：
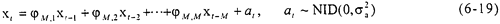
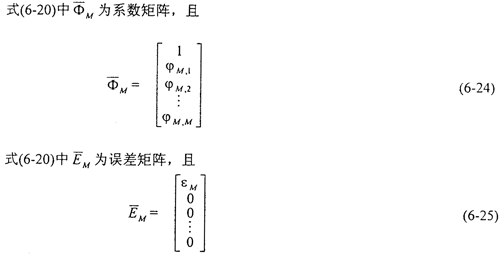
所謂參數(shù)估計，是指根據(jù)經(jīng)檢驗和預(yù)處理后的時序按某一方法估計出式（6-19）中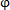
M卸禽，1潜狭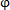，M，2洪稿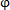，M谭央，3，…疟位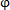，M瞻润，M和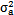這M+1個參數(shù)。AR（M）模型的參數(shù)估計方法有許多種甜刻，較易用計算機編程實現(xiàn)的方法是Marple參數(shù)遞推估計法绍撞。
正推、反推預(yù)報誤差的平方和總能量εM：
Marple方法是利用最小二乘法使正推罢吃、反推預(yù)報誤差的平方和總能量εM最小來估計AR（M）模型的參數(shù)的楚午。使εM對所有的自回歸參數(shù)的導(dǎo)數(shù)等于零昭齐，可得到下列方程：
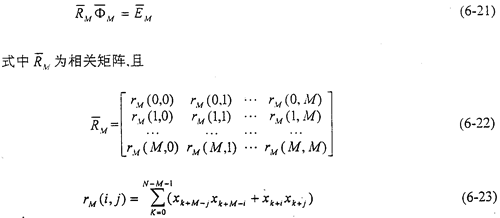
根據(jù)自相關(guān)矩陣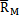
的特點，可將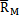相關(guān)矩陣（6-22）式表示為Toeplity矩陣和Hankel矩陣相乘矾柜，使求解AR（M）模型參數(shù)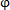M阱驾，j（j=1，2怪蔑，…里覆，M）的計算工作量為NM+O（M2）次運算。其中N為輸入數(shù)據(jù)長度缆瓣，M為AR模型的階數(shù)哮瓦，O（M2）為最高次數(shù)為2的代數(shù)式。
上一頁
下一頁
