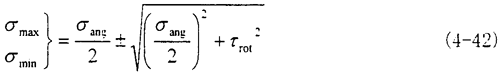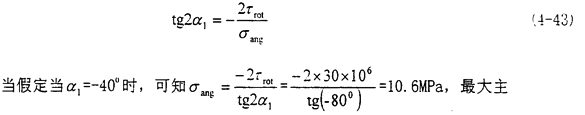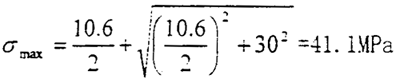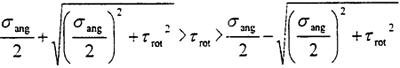4.5 角向不對中時的聯(lián)軸器的工作狀態(tài)
角向不對中時峡黍，由于兩軸之間存在一定的夾角卢掖，使得橡膠圓環(huán)最上方受到附加的拉應(yīng)力抗果，而圓環(huán)的最下端則受到附加的壓應(yīng)力吟沮，這個附加的拉應(yīng)力σang的大小和方向隨著圓環(huán)的旋轉(zhuǎn)角度改變而改變潜叛，在最上方時受拉谍钝，且絕對值最大批先，在最下方受壓，絕對值亦最大廊畔，所以其變化的過程圖形類似于余弦函數(shù)影其；由橡膠圓環(huán)旋轉(zhuǎn)扭矩產(chǎn)生的剪應(yīng)力τrot方向始終與其線速度方向相反，而線速度方向在旋轉(zhuǎn)一周的過程中不斷的變化任础。角向不對中時的應(yīng)力情況應(yīng)該是σang與τrot的疊加讲媚。所以其受力情況比較復(fù)雜。分別取四個象限點(diǎn)的位置狀態(tài)作為研究重點(diǎn)焰究，分別對單元體進(jìn)行應(yīng)力分析。
(1）角向不對中900位置：當(dāng)圓環(huán)上的單元體旋轉(zhuǎn)到最上方時怒详，也就是900位置時炉媒，單元體的應(yīng)力如下圖所示
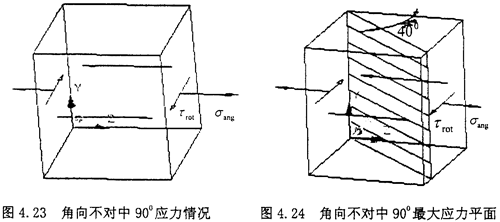
此時的受力情況其實(shí)屬于二向應(yīng)力狀態(tài)，即為拉扭結(jié)合昆烁，
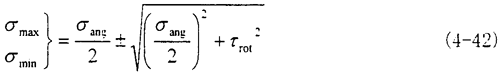
此時主平面上的正應(yīng)力平面的角度有這種關(guān)系
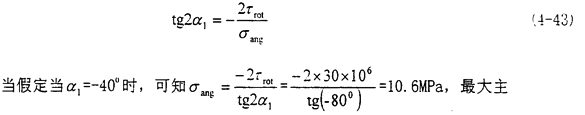
應(yīng)力平面如圖4.24所示吊骤。此時的最大應(yīng)力值為
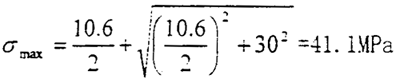
（2）角向不對中180°位置：當(dāng)圓環(huán)上的單元體旋轉(zhuǎn)到最左端時，也就是180°位置時静尼，單元體的應(yīng)力如下圖所示
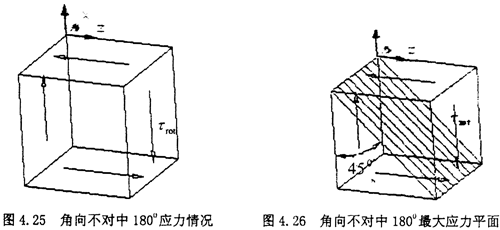
此時的受力圖中可以看出白粉，附加的拉應(yīng)力已經(jīng)減小為零，實(shí)際上單元體受力其實(shí)屬于純剪切狀態(tài)鼠渺，
此時主平面上的正應(yīng)力平面的角度有這種關(guān)系：tg2α2=-∞鸭巴，所以有α2=-45°或-135°，最大主應(yīng)力值為σmax=30MPa
（3）角向不對中270°位置：當(dāng)圓環(huán)上的單元體旋轉(zhuǎn)到最下方時拦盹，也就是270°位置時鹃祖，單元體的應(yīng)力如下圖所示
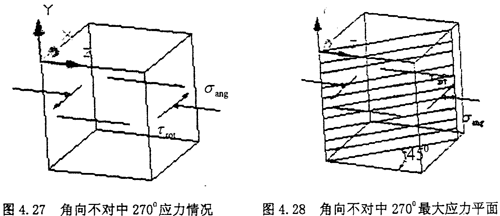
此時的受力情況其實(shí)屬于二向應(yīng)力狀態(tài)，只是這時的附加應(yīng)力變成了壓應(yīng)力普舆。即拉應(yīng)力變成了負(fù)號恬口。利用拉扭結(jié)合時的應(yīng)力分析方程可知
（4）角向不對中360°位置：當(dāng)圓環(huán)上的單元體旋轉(zhuǎn)到最右端時，也就是360°位置時速痹，單元體的應(yīng)力如下圖所示
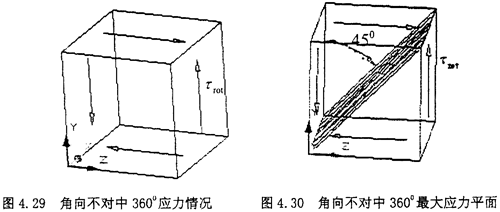
此時的受力圖中可以看出裂蝉，附加的拉應(yīng)力已經(jīng)減小為零，實(shí)際上單元體受力其實(shí)屬于純剪切狀態(tài)锦镶，
此時主平面上的正應(yīng)力平面的角度有這種關(guān)系：tg2α4=-∞虑庇，所以有α4=-45°或-135°，此時的最大應(yīng)力值為σmax=30MPa
通過角向不對中的分析可以知道拉狸，具有角向不對中的聯(lián)軸器受力情況仍然屬于兩向應(yīng)力狀態(tài)盾峭，即只有拉扭結(jié)合與純剪切的情況發(fā)，沒有三向應(yīng)力狀態(tài)，比較四個位置的最大主應(yīng)力
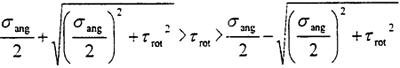
可以知道甫碉，在聯(lián)軸器旋轉(zhuǎn)一周的過程中碗履，最大主應(yīng)力在90°位置。即90°位置為角向不對中時的危險點(diǎn)蝗质。
4.6 綜合不對中時的聯(lián)軸器的工作狀態(tài)
綜合三種不對種情況勾萌，對圓環(huán)的單元體進(jìn)行綜合受力分析。由于實(shí)際工作中聯(lián)軸器兩軸之間不僅存在一定的徑向和軸向位移沈机，而且存在一定的偏角仙蛉。使得橡膠圓環(huán)受到附加的軸向拉應(yīng)力σax，附加的徑向剪應(yīng)τrad碱蒙，附加的角向應(yīng)力σang荠瘪，以及由橡膠圓環(huán)旋轉(zhuǎn)扭矩產(chǎn)生的剪應(yīng)力τrot。所以綜合不對中的應(yīng)力情況應(yīng)該是σax赛惩、τrad哀墓、σang與τrot的疊加。所以其受力情況比較復(fù)雜喷兼。仍然按照上面類似的方法分別取四個象限點(diǎn)的位置狀態(tài)作為研究對象篮绰，分別對單元體進(jìn)行應(yīng)力分析。
(l）綜合不對中90°位置：當(dāng)圓環(huán)上的單元體旋轉(zhuǎn)到最上方時季惯，也就是90°位置時吠各，單元體的應(yīng)力如下圖所示
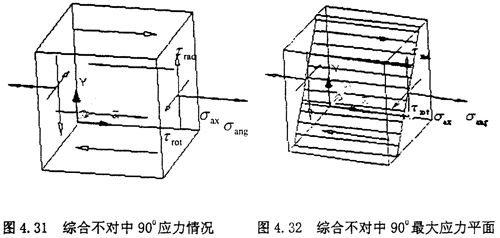
此時的應(yīng)力情況屬于三向應(yīng)力狀態(tài)，所以其分析過程和徑向不對中90°以及270°以情況相似勉抓，只是這里還有了附加的軸向拉應(yīng)力和附加的角向應(yīng)力贾漏，將各個應(yīng)力值σxx=σax+σang，σyy=0琳状，σzz=0伶葵，τxy=τrot，τyz=0菜册，τzx=τrad分別代入式（4-29）（4-30）（4-31）中蕴续，可以得到
I1=σax+σang+0+0=σax+σang
I2=0+0+0-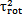
-0-
=-
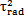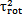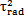
I3=0-0-0-0+0=0
再將三個應(yīng)力不變量代入方程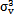
- I1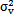
+ I2σv- I3=0中，得到
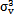-（σax+σang）-（
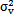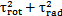）σv=0 （4-48）
解出這個方程蓄棘，可以得到三個主應(yīng)力的值
上一頁
下一頁
