3 雙環(huán)減速器環(huán)板內齒接觸分析及齒輪系統(tǒng)模態(tài)分析
3.1 雙環(huán)減速器環(huán)板內齒接觸有限元分析
因為在少齒差內嚙合中,不處于嚙合位置的齒對在進入嚙合之前以及在脫離嚙合之后讹蘑,其內、外齒廓間的間隙非常小狸眼,因此雙環(huán)減速器環(huán)板內齒輪嚙合傳動在載荷作用下杂数,因彈性變形實際接觸齒對數遠大于理論重合度妙旅,在傳遞載荷的過程中撼柳,輪齒的變形量要大于一部分齒對的間隙,這些齒對就要接觸并同時分擔載荷劫伊,這就大大提高了整個齒輪傳動裝置的承載能力拆聋。同時實際齒輪的接觸對數及接觸應力,隨著載荷增大而相應增加姊呐。因而少齒差內嚙合行星齒輪傳動的實際接觸齒對數的確定懒披,對齒輪承載能力的估算以及齒輪模數的正確確定具有重要意義。對于齒輪的接觸問題的翻默,國內外學者對此已作了不少研究缸沃,取得一些研究成果。然而這些研究有的沒有考慮誤差的影響修械,有的僅考慮內外嚙合齒輪副齒廓理論間隙,沒有考慮輪齒制造誤差和輪齒的彈性變形的影響检盼。本文對于環(huán)板內齒輪接觸問題進行了計算肯污,計算時考慮內外嚙合齒輪副齒廓理論間隙、制造誤差及輪齒彈性變形的影響吨枉,在此基礎上蹦渣,建立了少齒差內嚙合行星齒輪傳動實際接觸齒對數及各齒間載荷分配的理論分析計算的實體模型,利用I-DEAS軟件進行了環(huán)板內齒輪接觸有限元計算貌亭,并用該軟件分析計算了在不同載荷工況下的實際接觸齒對數柬唯、最大接觸應力以及兩環(huán)板上各接觸齒的載荷分配情況。
3.1.1 誤差對直齒內嚙合傳動重合度的影響分析
通常圃庭,內嚙合漸開線齒輪的理論計算是按無側隙的情況設計的锄奢,但要保證齒輪傳動靈活,不發(fā)生卡滯剧腻,必須保留足夠的齒側間隙工划,在實際制造與安裝中齒輪系統(tǒng)都必然存在尺寸誤差,這些誤差直接影響著齒輪傳動的精度占找、齒輪的強度和振動噪聲恒左。
眾所周知,內嚙合直齒圓柱齒輪傳動的理論重合度為:
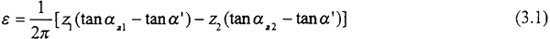
設內齒直齒輪傳動的齒輪模數為m络务,分度圓壓力角為a蔬旋,外齒輪齒數為Z1,內齒輪齒數為Z2怠鲜,外哩疲、內齒輪變位系數分別為X1霹链、X2,外里淡、內齒輪變位系數分別為S1′刃伞、S2′,外谎跨、內齒輪節(jié)圓上的齒槽寬分別為e1′钥嫌、e2′,兩嚙合齒輪節(jié)圓上的圓周側隙為jt男杈,兩嚙合齒輪非工作側齒廓沿公法線方向的側隙(法向側隙)為jn丈屹。顯然有
jn=jtcosα′=(e2′-s1′)cosα′ (3.2)

聯系式3.6與式3.8,從兩工中可以看出伶棒,計算中心距a′與嚙合角α′是一一對應關系旺垒,這樣式3.6可以表達為三種形式:
(1)由確定的齒側間隙jn與齒輪變位系數X2-X1來求中心距a′;
(2)由確定的中心距a′與齒輪變位系數X2-X1來求齒側間隙jn肤无;
(3)由確定的齒側間隙jn與中心距a′來求齒輪變位系數X2-X1先蒋。
當齒輪傳動的幾何設計參數確定后,影響實際傳動的就只有制造和安裝誤差宛渐,對于中心距a′而言竞漾,影響它的因素是制造誤差、安裝誤差窥翩,而不是齒側間隙jn與齒輪變位系數X2-X1业岁。齒輪設計是按無側隙進行的,同時不考慮制造寇蚊、安裝誤差笔时,但加工時,齒輪齒厚公差都是負偏差厕斩,即齒輪厚公差都是負偏差辨头,即齒輪必須減薄,這樣實際傳動存在齒側隙资妇。如果不考慮中心距的誤差娱背,由式3.6的第3種形式可知,齒側隙的變化必然影響到齒輪變位系數的變化水矢。顯然烂秘,這樣的變化也就會使齒輪的齒頂圓產生變化,相應的齒頂圓奢力角產生變化巩顶,進而影響齒輪嚙合重合度裳雕。
由式3.5變化為
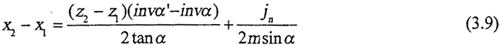
本文實驗樣機的環(huán)板齒輪設計參數見表3.1所示,根據本文實驗樣機的環(huán)板齒輪設計參數,假定嚙合角不變化帜浇,則對應齒側隙的變化辨蓄,應用MATLAB繪圖分析,得到了齒輪變位系數隨齒側隙變化時的變化規(guī)律圖项茸,見圖3.1所示祠乃。
表3.1 內嚙合齒輪參數表
|
外齒輪 |
環(huán)板內齒 |
模數 |
2 |
齒數 |
56 |
58 |
嚙合角 |
39.039° |
變位系數 |
1.37 |
1.685 |
齒頂高系數 |
0.7 |
中心距 |
2.42 |
齒頂圓直徑 |
119.519 |
120.774 |
計算重合度 |
1.124 |
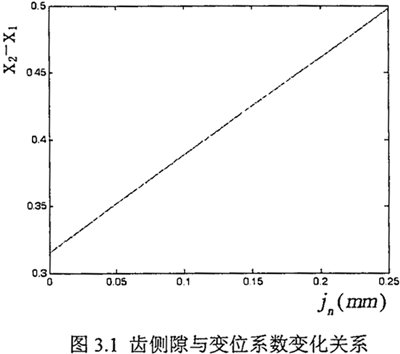
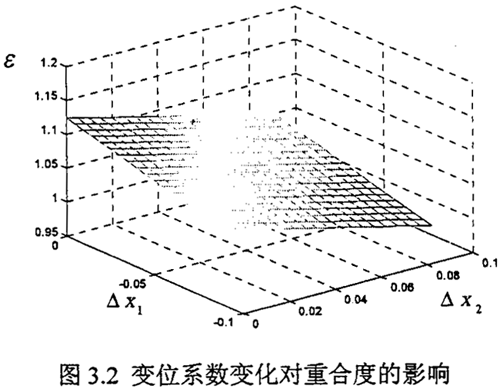
由3.2圖可以看出,當齒側隙jn由0變化至.25毫米時(查資料取較大最小側隙參考值)兑燥,齒輪變位系數差X2-X1的變化量由近0.32變化到0.50亮瓷,變化了約0.18。
對于齒頂圓直徑按德國工業(yè)標準DIN的簡單方法有:
da1=m(z1+2ha*+2x1) (3.10)
da2=m(z2+2ha*+2x2) (3.11)
由式3.10降瞳、3.11可以看出嘱支,當總變位系數xΣ=x2-x1產生變化時,必然引起起嚙合齒輪齒頂圓直徑的變化挣饥。按X1除师、X2變化最小原則,有三種可能性扔枫,即X1不變汛聚,X2變化0~0.18;或X1變化0~0.18短荐,X2不變贞岭;或X1變小,X2變大搓侄,變化范圍0~0.09。假定齒輪嚙合角不變予乏,按本文實驗樣機參數偿寥,當齒輪變位系數發(fā)生變化時,其變化量對重合度的影響狀況見圖3.2所示蟹游。從圖3.2所示可以看出填级,隨外齒輪變位變小時,齒輪嚙合重合度減小蔓捡,隨內齒輪變位變小時怜人,齒輪嚙合重合度增大,從圖中的變化趨勢為看擦灸,外齒輪變位系數的變化對重合度的影響程度與內齒輪變位系數的變化對重合度的影響程度大約是相同的癌羞,只是趨向是反向的。
對于中心距而言剂撑,查資料表35.2-60可知中心距的極限偏差為±0.011mm,假定外齒輪齒頂圓壓力角不變豌富,內齒輪齒頂圓壓力角隨變位系數變化,對于中心距變化對重合度的影響變化趨勢及變位系數變化對重合度的影響的變化趨勢比較情形見圖3.3苞毡。假定內齒輪齒頂圓壓力角不變铅乡,外齒輪齒頂圓壓力角隨變位系數變化继谚,對于中心距變化對重合度的影響變化趨勢及變位系數變化對重合度的影響的變化趨勢比較情形見圖3.4所示。
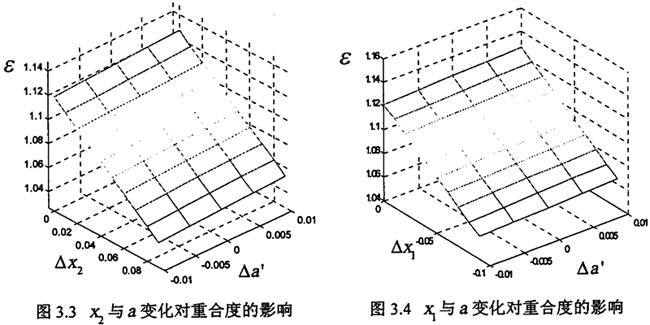
從圖3.3阵幸、3.4明顯看出中心距變化對重合度的影響程度明顯小于變位系數變化對重合度的影響程度花履。
齒輪制造誤差中對齒廓間隙影響較大的有最小齒側間隙、基節(jié)偏差挚赊、齒形誤差诡壁、齒距偏差、齒厚偏差等等咬腕,但這些因素相互關聯欢峰、相互制約、相互影響涨共,特別是基節(jié)偏差纽帖、齒形誤差、齒距偏差举反、齒厚偏差等最終影響齒側隙的變化懊直,因此最終影響齒輪傳動的主要因素仍是中心距和齒側隙的變化。分析圖3.2火鼻、3.3旱醉、3.4,在允許的制造誤差范圍內及最小齒側隙的情況下穗蚌,重合度的理論計算值變化不是很大敬育。
3.1.2 接觸分析中制造安裝誤差的引入
從上述分析可知,齒輪的制造崭守、安裝誤差對齒輪嚙合的重合度有一定的影響零勃,但就理論計算值而言,從上面的分析結果可以看出其影響程度是不大的浙辫,然而在少齒差內嚙合齒輪副中类菊,嚙合線附近兩相鄰工作齒對齒側間隙非常小。假設內齒輪固定郊檐,當輪齒承擔載荷時玩捉,兩接觸輪齒將分別產生彈性變形,外齒輪將繞其軸線旋轉一附加角茴怀,當這一附加轉角足夠大時词宴,除原有接觸齒對繼續(xù)發(fā)生接觸外,相鄰工作齒對的齒側間隙也會消失寺晌,這樣就產生了多齒承載接觸世吨。
在本節(jié)中,引入制造、安裝誤差耘婚,用有限元方法計算內齒傳動的接觸對數罢浇,同時驗證上節(jié)中討論的影響重合度的關鍵參數。用I-DEAS軟件計算環(huán)板內齒接觸問題沐祷,其關鍵是齒輪輪齒的實體建模嚷闭。對于相嚙合的齒輪,因其兩工作齒廓側面相互位置誤差的變化導致了實際齒廓間隙的變化赖临,在嚙合線附近只有少數幾對齒在我們討論范圍內胞锰,這里我們只考慮對齒廓間隙影響較大的最小齒側間隙、基節(jié)偏差兢榨、齒形誤差嗅榕、齒距偏差、齒厚偏差等吵聪。在用用I-DEAS軟件進行齒輪輪齒的實體建模時凌那,對輪齒而言,沿圓周是均勻分布的嫌盲,因此董记,齒輪的制造誤差在實體造型時,表現在齒輪輪齒的齒厚及基圓尺寸的誤差上赐赁。而經多元回歸分析檀塌,得出各變量對齒廓間隙的內在影響關系表明:齒輪的基節(jié)偏差是最主要的影響因素。
本文雙環(huán)減速器齒輪加工精度為7級雕踊,根據資料前河,查得齒輪的基節(jié)極限偏差△fpb為±0.014,對于齒厚極限偏差挺候,根據資料您风,查得齒輪齒厚的極限偏差△Es的上偏差為-128μm,下偏差為-192μm京球,將這些影響因素的極限偏差,通過幾何關系的轉換腺帽,換算到基節(jié)上怎晰,通過參數方程繪出齒輪單個輪齒的輪廓線,再由單個輪齒的齒廓沿圓周接齒輪齒數均勻復制敛苇,這樣得到整個齒輪的齒廓線妆绞,由齒廓線延伸成齒輪實體模型。
由于零部件的制造誤差枫攀,同時因裝配原因括饶,在進行整體裝配時,產生零部件間的安裝誤差,這些誤差直接影響齒輪間的嚙合狀態(tài)图焰。對于雙環(huán)減速器中的環(huán)板內齒輪嚙合傳動启盛,由于環(huán)板內齒中心與輸出齒輪中心之間的偏心距尺寸較小(本文雙環(huán)減速器的偏心距為2.42mm)技羔,因此僵闯,偏心軸的偏心距制造誤差及中心距制造安裝誤差是影響環(huán)板內齒嚙合傳動的關鍵。本文雙環(huán)減速器兩偏心軸偏心距的制造誤差為±0.011藤滥。
綜合以上誤差分析鳖粟,將環(huán)板與輸出齒輪軸按極限偏差尺寸所定的位置進行輪齒嚙合裝配,然后進行有限元接觸分析拙绊。
3.1.3 齒輪有限元模型的建立及邊界條件的確定
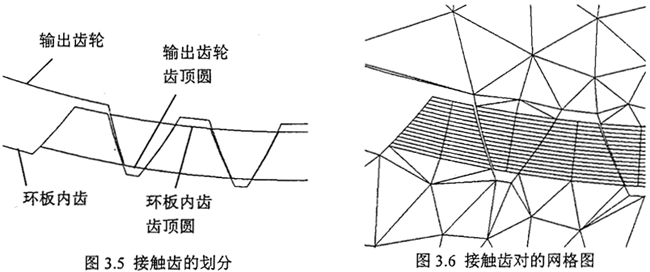
環(huán)板內齒輪與輸出軸齒輪之間的傳動是直齒輪傳動向图,為保證進行接觸計算時,有較多的有較接觸區(qū)域哟俩,齒輪輪齒部分的有限元網格采用映射網格劃分法(Mapped Meshing)對齒輪進行有限元網格劃分碉讯。同時,為保證兩對嚙合齒輪所劃分的網格接觸對相應的面能對應齊咸壮,因此齒輪嚙合的接觸面相應應當齊整拿奥。用輸出軸齒輪的齒頂面所在的輪廓曲面對環(huán)板內齒進行劃分(partition 命令),同理用環(huán)板內齒的齒頂面所在的輪廓曲面對輸出軸齒輪進行劃分漆究,這樣得到對應齊整的齒輪嚙合的接觸面母滤,如圖3.5所示。根據圖3.5所示钉榔,采用映射網格劃分法( Mapped Meshing)進行網格劃分的輪齒部分即是圖中輸出齒輪齒頂圓與環(huán)板內齒齒頂圓之間所劃分的部分城砖,而其余部分采用自由網格劃分法(Free Meshing)進行劃分,劃分網格后的部分網格圖見圖3.6所示圣钝⊥⑴担考慮實際接觸齒對數不會太多,所以每塊環(huán)板上只給出6個輪齒進行接觸計算肖喂。環(huán)板嚙合的實際過程是環(huán)板齒輪帶動輸出齒輪運動簇抵,計算時為方便,假設環(huán)板固定不動射众,設定輸出軸繞軸線轉動碟摆,將減速器的輸出功率換算為輸出扭矩,加在輸出軸的輸出端叨橱。
3.1.4 接觸計算結果分析
按考慮偏心距誤差影響及考慮齒厚誤差影響的兩個極限狀態(tài)典蜕,組合為十種情況進行計算。十種計算工況見表3.2所示罗洗∮涮颍考慮齒厚誤差影響的兩個極限狀態(tài)分別是齒輪的輪齒最薄钢猛、最厚,偏心距誤差的兩個極限狀態(tài)分別是偏心軸的偏心距最大轩缤、最小兩種情況命迈。種接觸情況的計算結果分別由表3.3~3.7列出。
3.2計算工況列表
| 序號 |
工況說明 |
序號 |
工況說明 |
| 齒厚狀態(tài) |
偏心距狀態(tài) |
兩環(huán)板狀態(tài) |
齒厚狀態(tài) |
偏心距狀態(tài) |
兩環(huán)板狀態(tài) |
| 1 |
最厚 |
無誤差 |
對稱 |
6 |
最薄 |
最大正偏差 |
對稱 |
| 2 |
最薄 |
無誤差 |
對稱 |
7 |
最厚 |
最大負偏差 |
不對稱 |
| 3 |
最厚 |
最大負偏差 |
對稱 |
8 |
最薄 |
最大負偏差 |
不對稱 |
| 4 |
最薄 |
最大負偏差 |
對稱 |
9 |
最厚 |
最大正偏差 |
不對稱 |
| 5 |
最厚 |
最大負偏差 |
對稱 |
10 |
最薄 |
最大正偏差 |
不對稱 |
3.4工況一接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況一 |
200 |
1 |
1 |
75.2 |
| 160 |
1 |
1 |
66.8 |
| 120 |
1 |
1 |
56.1 |
| 80 |
1 |
1 |
41.1 |
| 40 |
1 |
1 |
28.0 |
3.5工況二接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況二 |
200 |
1 |
1 |
75.2 |
| 160 |
1 |
1 |
66.8 |
| 120 |
1 |
1 |
56.1 |
| 80 |
1 |
1 |
41.1 |
| 40 |
1 |
1 |
28.0 |
3.6工況三接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況三 |
200 |
1 |
1 |
68.2 |
| 160 |
1 |
1 |
62.6 |
| 120 |
1 |
1 |
55.1 |
| 80 |
1 |
1 |
40.2 |
| 40 |
1 |
1 |
25.3 |
3.7工況四接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況四 |
200 |
2 |
2 |
74.6 |
| 160 |
2 |
2 |
62.1 |
| 120 |
2 |
2 |
49.0 |
| 80 |
2 |
2 |
41.8 |
| 40 |
1 |
1 |
26.6 |
3.8工況五接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況五 |
200 |
2 |
2 |
2.2 |
| 160 |
2 |
2 |
58.6 |
| 120 |
2 |
2 |
45.6 |
| 80 |
2 |
2 |
42.1 |
| 40 |
1 |
1 |
26.5 |
3.9工況六接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況六 |
200 |
1 |
1 |
76 |
| 160 |
1 |
1 |
63.2 |
| 120 |
1 |
1 |
49.7 |
| 80 |
1 |
1 |
40.5 |
| 40 |
1 |
1 |
28.5 |
3.10工況七接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
| 工況七 |
200 |
1 |
3 |
76 |
| 160 |
0 |
2 |
63.2 |
| 120 |
0 |
2 |
49.7 |
| 80 |
0 |
1 |
40.5 |
| 40 |
0 |
1 |
28.5 |
3.11工況八接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
工
況
八 |
200 |
1 |
2 |
130.0 |
| 160 |
0 |
2 |
114.0 |
| 120 |
0 |
2 |
93.4 |
| 80 |
0 |
2 |
70.2 |
| 40 |
0 |
2 |
39.0 |
3.12工況九接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
工
況
九 |
200 |
2 |
1 |
104.0 |
| 160 |
2 |
0 |
92.6 |
| 120 |
2 |
0 |
86.6 |
| 80 |
2 |
0 |
65.3 |
| 40 |
1 |
0 |
42.8 |
3.13工況十接觸情況計算表
| 誤差情況 |
載荷(N·m) |
接觸齒對數 |
最大接觸應力(MPa) |
| 環(huán)板1 |
環(huán)板2 |
工
況
十 |
200 |
2 |
1 |
136.0 |
| 160 |
2 |
0 |
117. |
| 120 |
2 |
0 |
102.0 |
| 80 |
2 |
0 |
77.4 |
| 40 |
2 |
0 |
47.6 |
由表3.2~3.13可以看出典奉,無論有無制造躺翻、安裝誤差的影響,隨著負荷的增加卫玖,齒輪實際嚙合接觸對數增加真葱,但從計算結果分析證明,負荷對接觸對的影響小于誤差對接觸對的影響辐胆。對比表中的接觸對數和接觸應力讨砍,數據表明當齒厚發(fā)生變化時,實際接觸齒對數變化比較大卸研,同時最大接觸應力也有明顯變化佩讨。從變化的趨勢上看出與前面的理論推導變化趨勢相同,這里只是更加明顯多盅。
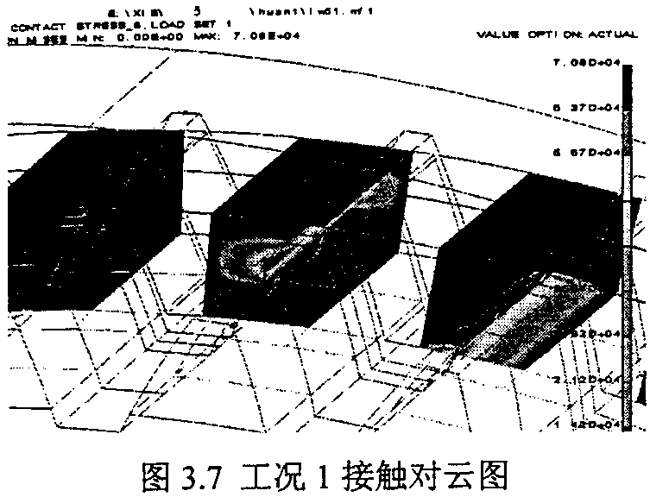
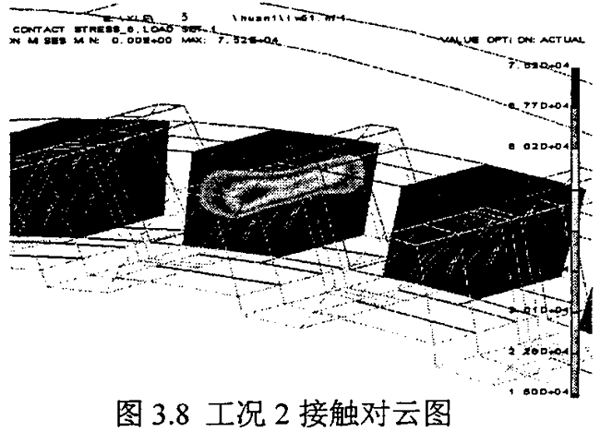
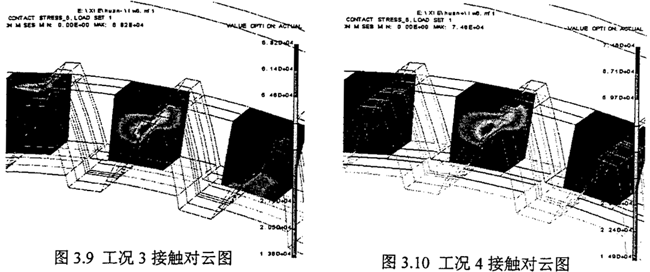
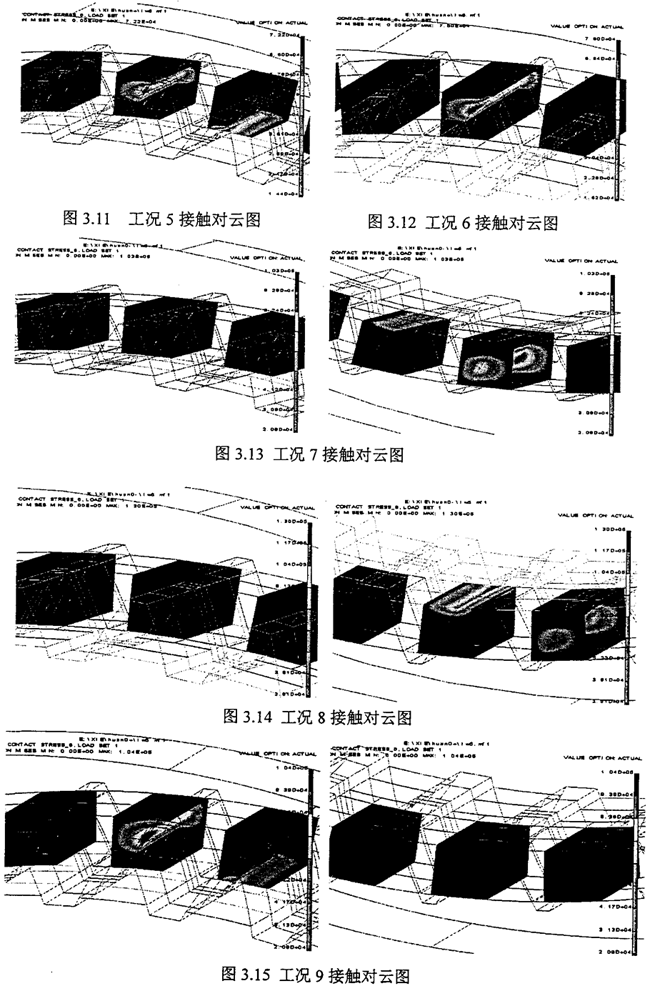
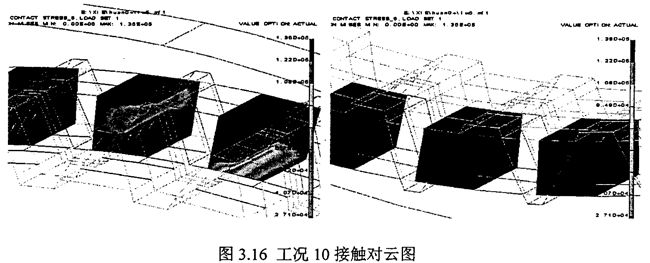
工況六至工況十這四和情況把毒,是指兩環(huán)板之間不對稱,即偏心軸的兩個偏心拐的尺寸誤差不一致勤右,這里考慮的是特殊狀況徽捶,從表3.10-3.13看出,當兩環(huán)板不對稱時虫甲,將產生嚴重的載荷不均現象淡箱,載荷偏向中心距小的環(huán)板內齒上,甚至只有一個環(huán)板承受載荷辩块。由此說明蛔六,對于雙環(huán)減速器偏心軸有加工,應特別注意兩曲捌的制造誤差废亭,應盡量使安裝好的兩環(huán)板具有較好的對稱性国章。圖3.7~圖3.12為六種工況下環(huán)板內齒的接觸齒對的應力云圖。
3.2 雙環(huán)減速器有限元模型建立及模態(tài)分析
近年來豆村,隨著齒輪振動噪聲研究的不斷深入捉腥,不僅需要考慮齒輪系統(tǒng)及其嚙合過程,還必須考慮動態(tài)嚙合力在整個齒輪系統(tǒng)中的傳遞你画,以及系統(tǒng)中各零部件的固有特性和動態(tài)響應的性質,因此桃漾,必須以整個齒輪系統(tǒng)為研究對象坏匪,建立同時包括傳動系統(tǒng)和結構系統(tǒng)的完整系統(tǒng)的分析模型拟逮。本節(jié)將在雙環(huán)減速器運動特性分析的基礎上,以整個雙環(huán)減速器齒輪系統(tǒng)為對象适滓,建立有限元動力分析模型敦迄,全面分析該系統(tǒng)的固有特性和動態(tài)響應。
齒輪系統(tǒng)的固有特性一般指系統(tǒng)的固有頻率和固有振型番恭,是齒輪系統(tǒng)的動態(tài)特性之一奖岛,它對系統(tǒng)的動態(tài)響應,動載荷的產生與傳遞坠诈,以及系統(tǒng)振動的形式等都具有重要意義淑储。此外,固有特性還是用振型疊加法求解系統(tǒng)響應的基礎扯氯。由于系統(tǒng)的固有特性表明了在哪些頻率下結構會產生共振以及在各階頻率下結構的相對變形俏堆,因此對于改善結構動態(tài)特性具有重要意義。通常烟内,研究齒輪系統(tǒng)固有特性有理論計算法和實驗測試法兩種篡呆。實驗測試將在以后的章節(jié)中研究,本章將利用數值計算法計算雙環(huán)減速器齒輪系統(tǒng)的固有特性面旋。結構系統(tǒng)固有特性的數值計算通常采用有限元模態(tài)分析方法摇龟。在有限元分析中,結構的動力學特征用微分方程組表征吟沮,則結構的固有頻率和固有振型相應地由動力學方程的特征值和特征向量所確定遮乾。所以可以說,求系統(tǒng)的固有頻率和固有振型即為求系統(tǒng)的特征值和特征向量糙箍。特征值問題的解法很多渤愁,主要有多項式割線迭代法、矢量逆迭代法深夯、廣義雅可比法抖格、子空間迭代法和行列式收縮法。動力問題有限元法是求解復雜結構的大型動力學方程組的特征值問題的有效方法咕晋。本章將用動力有限元法對雙環(huán)減速器齒輪系統(tǒng)進行特征值分析雹拄,計算其固有頻率和固有振型。
本文建立了齒輪系統(tǒng)的有限元動力學模型掌呜,用I-Deas 集成化軟件的固有模態(tài)求解模塊求解了齒輪系統(tǒng)的固有頻率和振型滓玖,并用響應動力(Response Dynamios)分析模塊研究了齒輪傳動系統(tǒng)的動態(tài)響應特性。要進行有限元模態(tài)分析质蕉,必須先建立齒輪系統(tǒng)的有限元力學模型势篡。
上一頁
下一頁










