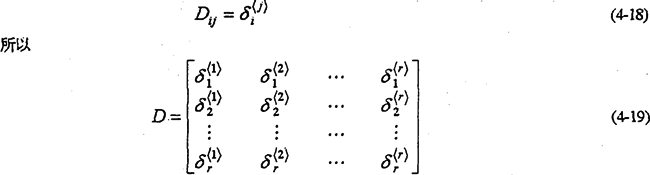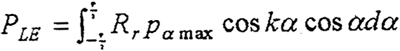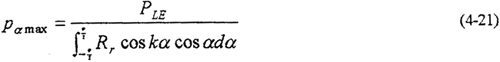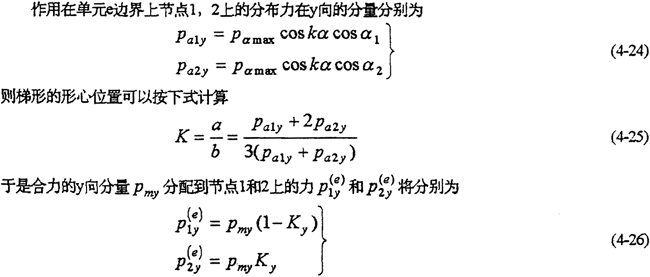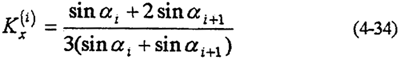內(nèi)齒行星齒輪傳動(dòng)零件的變形位移研究
4.1引言
上一章對(duì)內(nèi)齒行星齒掄傳動(dòng)機(jī)構(gòu)的動(dòng)力建模進(jìn)行了系統(tǒng)的研究乒裆。從研究中發(fā)現(xiàn)，建立位移協(xié)調(diào)補(bǔ)充方程時(shí)，都必須將變形位移與構(gòu)件的柔度或剛度聯(lián)系，變換成真正要求解的力或力矩的關(guān)系或详。對(duì)結(jié)構(gòu)簡(jiǎn)單的軸類零件以及齒輪等，可以利用現(xiàn)有的有關(guān)計(jì)算公式直接建立變形位移與力握）的關(guān)系。然而對(duì)于行星齒板徊岂、偏心套等零件，由于其結(jié)構(gòu)形狀復(fù)雜只能將變形按接觸變形進(jìn)行處理报叁，即用接觸力與接觸剛度系數(shù)之比代換位移田漓。這種方法簡(jiǎn)便，可以直接導(dǎo)出解的結(jié)果付找。適合于載荷不大歧胃，零件變形小的傳動(dòng)。但對(duì)于重載高速傳動(dòng)來(lái)說(shuō)艰争，零件的總體變形往往比較大坏瞄，特別是行星齒板的齒圈厚度是隨位置角度變化的，其變形也將隨嚙合齒變化而變化园细。
因此惦积，齒板的剛度在工作過(guò)程中變化也很大，不可能為常數(shù)猛频。行星齒板上某點(diǎn)的位移與作用在齒板上力（載荷）的關(guān)系并不象接觸變形那樣狮崩，某點(diǎn)的位移只與該點(diǎn)受載及該點(diǎn)柔度（剛度）有關(guān)。而是通過(guò)齒板的整體柔度系數(shù)矩陣聯(lián)系作用在齒板上所有外力來(lái)反映某點(diǎn)的位移鹿寻。把這種位移與力的關(guān)系叫做柔度方程睦柴。行星齒板柔度方程中的柔度系數(shù)，隨工況位置φ(j)變化毡熏，不是固定值坦敌。柔度系數(shù)可以在不同的工況時(shí)通過(guò)有限元法等數(shù)值計(jì)算方法來(lái)確定。本章用有限元法計(jì)算行星齒板及偏心套在不同工況時(shí)的柔度系數(shù)痢法，導(dǎo)出其位移與力的關(guān)系狱窘。對(duì)軸、軸承财搁、外齒輪等零件的位移與力的關(guān)系愈饲，用現(xiàn)有的理論公式表示。
4.2彈性體的柔度方程及其柔度計(jì)算
柔度方程亦是彈性體的位移表達(dá)式蝉丧。有限元法中的剛度方程就是彈性體節(jié)點(diǎn)位移與節(jié)點(diǎn)力之間的關(guān)系
由式（4-1）表達(dá)的是彈性體節(jié)點(diǎn)位移的隱函式碴纺。必須將其轉(zhuǎn)換只與彈性體外載荷有關(guān)的節(jié)點(diǎn)位移顯函式，才有用于內(nèi)齒行星齒輪傳動(dòng)的動(dòng)力分析中就留。由于式（4-1）中的總剛度矩陣K是一個(gè)奇異矩陣仇习，不存在逆矩陣何大，所以不能直接解出其位移表達(dá)式來(lái)。必須考慮實(shí)際邊界條件梆载，以及為避免出現(xiàn)剛體運(yùn)動(dòng)摇蝗，對(duì)具體的彈性體進(jìn)行某體節(jié)點(diǎn)零位移的約束處理。即對(duì)總剛度矩陣K要作相應(yīng)的變更自葡，使總剛度矩陣變?yōu)榉瞧娈惥仃嚺适摹Ｌ幚磉吔缥灰萍s束的方法見(jiàn)參考文獻(xiàn)。
經(jīng)過(guò)約束處理后恤仁，式（4-1）記作
式（4-6）就是彈性體離散化后坏榜，經(jīng)過(guò)約束處理的節(jié)點(diǎn)位移表達(dá)式，即彈性體的柔度方程隆檀。設(shè)約束處理后有n組節(jié)點(diǎn)位移摇天，即
式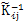
（i=1，2恐仑，…泉坐，n；j=1裳仆，2腕让，…，n）是彈性體柔度子矩陣歧斟。
所以柔度方程為
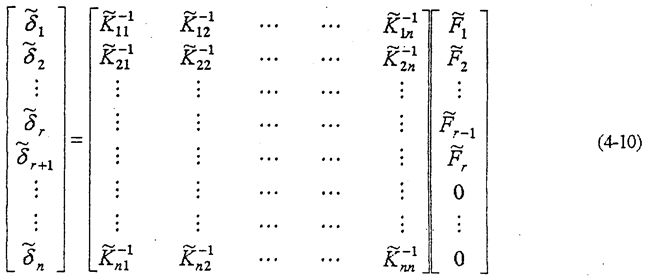
式（4-12）就是外力作用點(diǎn)位移及其作用力的關(guān)系式纯丸。
柔度矩陣戌構(gòu)件的材料、幾何形狀以及劃分網(wǎng)格形狀等因素有關(guān)静袖。其中各元素可以依次加單位載荷觉鼻，用式（4-12）計(jì)算確定。先令式（4-14）中F1=1队橙，F(xiàn)2=F3=…=Fr=0代入式（4-12）得
上式中Di1=δ<1>i就是F1作用點(diǎn)加單位載荷計(jì)算出的柔度系數(shù)值坠陈。同理可分別在F2，F(xiàn)3淮辕，…蘸错，F(xiàn)r作用點(diǎn)加單位載荷，求出其余的柔度
系數(shù)值俯炮，于是得到
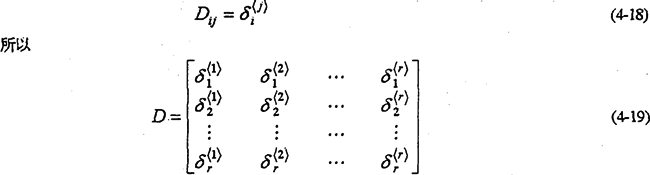
式（4-19）就是用有限元法通過(guò)加單位載荷求得的彈性體柔度矩陣
4.3偏心套及行星齒板的柔度計(jì)算
從上節(jié)介紹知苇恤，彈性體的柔度系數(shù)矩陣可以通過(guò)有限元法，加單位載荷來(lái)計(jì)算確定霹壁。因此，偏心套及內(nèi)齒行星傳動(dòng)齒板的柔度計(jì)算一步，實(shí)際上是對(duì)其進(jìn)行有限元建模分析剿稼。下面以SHQ40型三環(huán)傳動(dòng)為例，在SUN工作站上使用I-DEAS軟件中的有限元模塊計(jì)算偏心套及齒板的柔度系數(shù)。
4.3.1偏心套的有限元柔度計(jì)算
偏心套的實(shí)體模型如圖4-1所示茂禁。由于在三環(huán)傳動(dòng)中斩角，偏心套的兩側(cè)是由檔塊整面限制其位移，即有w=0瞻窗，εz=0伶丐，γzy=γzx=0，因此疯特，可以將偏心套簡(jiǎn)化為平面應(yīng)變問(wèn)題來(lái)處理哗魂。
圖4-1偏心套實(shí)體模型
用I-DEAS文件將實(shí)體模型傳輸?shù)接邢拊治鲕浖小Ｔ诖藥缀文Ｐ偷幕A(chǔ)上漓雅，對(duì)外圓周以每360°/5一個(gè)節(jié)點(diǎn)進(jìn)行等分录别，選用平面三角形單元，自動(dòng)生成如4-2所示的有限元網(wǎng)格圖邻吞。
由于偏心套是與高速軸直接套在一起组题，并通過(guò)鍵傳遞扭矩，計(jì)算偏心套的柔度時(shí)抱冷，可取偏心套與鍵接觸處節(jié)點(diǎn)法向位移崔列，以及偏心套內(nèi)圓與軸接觸處各節(jié)點(diǎn)的徑向位移為零（見(jiàn)圖4-2所示）。
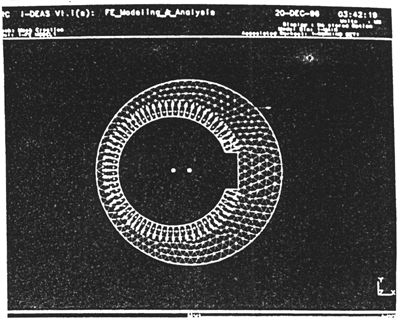
圖4-2偏心套網(wǎng)格及約束圖
齒板是通過(guò)軸承將力作用在偏心套的外圓周上旺遮，而且在不同的工況其接觸點(diǎn)不相同赵讯。因此，計(jì)算偏心套的柔度系數(shù)矩陣時(shí)趣效，需要對(duì)外圓周上的每個(gè)節(jié)點(diǎn)瘦癌，依次加單位載荷，計(jì)算出外圓周上每個(gè)節(jié)點(diǎn)的位移（亦其柔度系數(shù)值）绊叙。將這些柔度系數(shù)值整理成適合計(jì)算調(diào)用的磁盤文件PXTRD.DAT填丢。
4.3.2行星齒板的有限元柔度計(jì)算
行星齒板在內(nèi)齒行星傳動(dòng)中，既是雙曲柄機(jī)構(gòu)的連桿夸营，又是少齒差傳動(dòng)的內(nèi)齒輪敞灸，是傳遞運(yùn)動(dòng)及動(dòng)力的關(guān)鍵零件。齒板一般都是直齒圓柱齒輪贫介。其它零件與其接觸作用的力都是平行于齒板平面沿其厚度均布的区酷。在板面內(nèi)無(wú)任何外力作用，因此可以認(rèn)為板內(nèi)各點(diǎn)的六個(gè)應(yīng)力分量中所有沿Z方向（垂直于板聞）的分量均為零翠蓄，即有σz=τyz=τxz=0,剩下的三個(gè)分量σxσyτxy都是作用在和XOY平
面相平行的平面內(nèi)丛幌。行星齒板的實(shí)體模型如圖4-3所示。這樣抢纹，可以把對(duì)齒板的研究簡(jiǎn)化成平面應(yīng)力問(wèn)題來(lái)處理懒碍。
行星齒板的實(shí)體模型如圖4-3所示葱妒。將其傳輸?shù)接邢拊K中，以平面三角形單元進(jìn)行網(wǎng)格化分缝驳，如圖4-4所示连锯。高速軸孔的周邊節(jié)點(diǎn)數(shù)為360°/Z2。
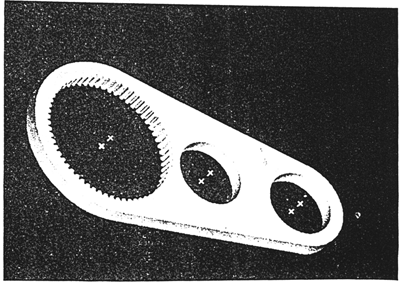
圖4-3齒板實(shí)體模型
由于在內(nèi)齒行齒輪傳動(dòng)動(dòng)力分析中用狱，計(jì)算的是外力作用點(diǎn)之間的相對(duì)位移运怖，因此，在對(duì)齒板進(jìn)行剛體位移約束時(shí)夏伊，約束水平位移的節(jié)點(diǎn)應(yīng)盡可能選在外力作用點(diǎn)之間的水平坐標(biāo)范圍之外摇展。約束鉛垂位移的節(jié)點(diǎn)應(yīng)盡可能選在外力作用點(diǎn)之間的垂直坐標(biāo)之外。這樣才不至于由于約束節(jié)點(diǎn)產(chǎn)生的反力影響外力作用點(diǎn)之間的相對(duì)位移署海。根據(jù)這個(gè)原則吗购，可令齒板最左端邊緣一節(jié)點(diǎn)的水平位移為零，以消除齒板的剛體水平位移砸狞；令齒板最上端邊緣一節(jié)點(diǎn)及中孔垂直對(duì)稱軸與齒板最上邊邊緣交點(diǎn)的節(jié)點(diǎn)位移為零捻勉，以消除齒板的剛體垂直位移和剛體角位移，如圖4-4 所示刀森。
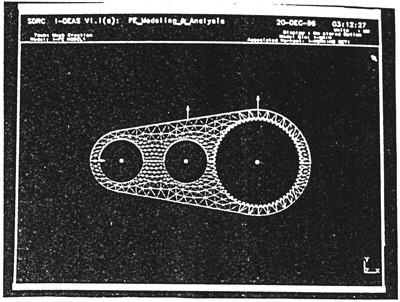
圖4-4齒板網(wǎng)絡(luò)及約束圖
單位載荷依次加在各高速軸孔內(nèi)圓周邊各節(jié)點(diǎn)踱启，以及與外齒輪嚙合的內(nèi)齒圈分度圓節(jié)點(diǎn)上，將求解出的柔度系數(shù)分為高速軸研底、內(nèi)齒圈兩大類庵恨，分別見(jiàn)磁盤文件GF1.DAT,GF2.DAT及GFN.DAT，GFN.DAT等修扁。
4.4偏心套和行星齒板的位移及其剛度系數(shù)
用有限元法計(jì)算出偏心套和齒板的柔度系數(shù)表后诀烫，就可以由式（4-12）寫出它們?cè)诓煌r時(shí)，關(guān)于嚙合力及軸承作用力的節(jié)點(diǎn)柔度方程組峡逆。但是勃拢，由軸承作用給偏心套及齒板高速軸孔的反力，是沿作用周邊非均布變化的念弧，而且作用范圍（接觸角）也很知道后涛。這給動(dòng)力分析帶來(lái)很大的困難。因此有必要對(duì)軸承作用給這兩個(gè)零件的節(jié)點(diǎn)載荷加以簡(jiǎn)化處里依播。
4.4.1軸承載荷的處理
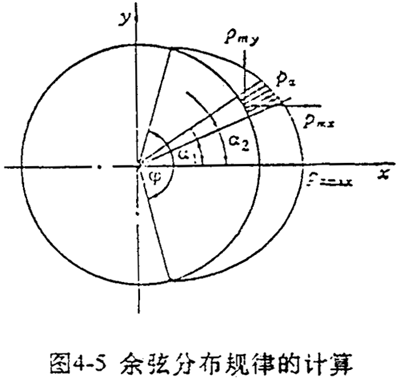
確定作用于結(jié)構(gòu)邊界上的非均布載荷是一件復(fù)雜工作口愁，往往需要進(jìn)行一些較復(fù)雜的計(jì)算，譬如采用接觸問(wèn)題有限元法進(jìn)行計(jì)算娱必。在實(shí)際應(yīng)用中常采用一些近似的假設(shè)規(guī)律來(lái)代替這些復(fù)雜的未知分布規(guī)律鸿挠。對(duì)于軸承載荷，一般假設(shè)沿周邊按余弦規(guī)律分布如圖4-5所示姻蚓，即
Pα= Pα maxcos Kα （4-20）
式中Pα二為分布載荷：
Pα max 為最大分布載荷宋梧；
由上式可寫出
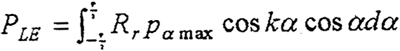
于是得到
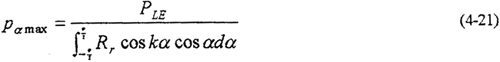
其中PLE為軸承負(fù)荷的合力秋茫；
Rr為偏心套或齒板孔半徑；
φ為接觸角乃秀。
系數(shù)K可按下式計(jì)算
當(dāng)α=φ/2時(shí)，由式（4-20）得知Pα為零：即Pα=Pα maxcosKα=0
當(dāng)分布規(guī)律求出以后圆兵，即可按下式計(jì)算接觸邊界上各節(jié)點(diǎn)之間微段上分布力的合力Pm及其X跺讯、Y軸方向上的分量Pmx和Pmy
然后，按靜力學(xué)等效原理殉农，將微段上的合力或其分量分別移置到對(duì)應(yīng)的邊界各節(jié)點(diǎn)上刀脏。因邊界上各節(jié)點(diǎn)之間的微段一般較短，可認(rèn)為各微段上的作用力近似梯形分布超凳，而Pmx愈污，Pmy就可以認(rèn)為是作用在梯形的形心上（圖4-6（a））。
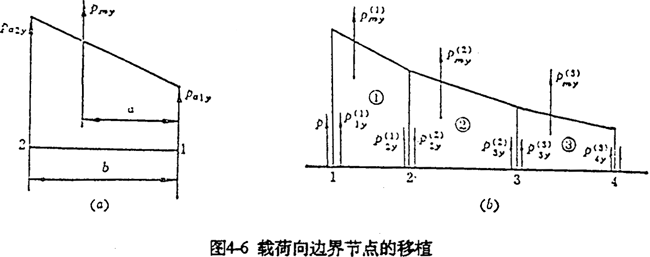
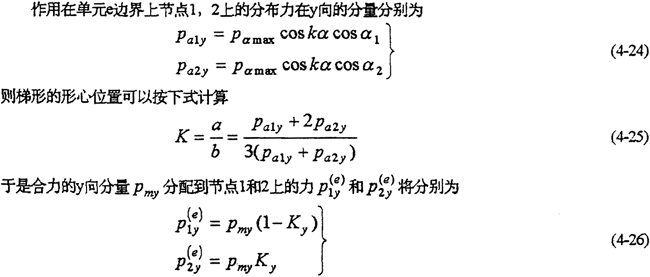
對(duì)于邊界上每一個(gè)微段轮傍，按上述方法計(jì)算完后暂雹，再對(duì)每一個(gè)邊界點(diǎn)處的力求和即得到邊界節(jié)點(diǎn)沿y向的載荷分量（圖4-6（b））。例如抱典，對(duì)于邊界節(jié)點(diǎn)2衔耕，其節(jié)點(diǎn)載荷P2y為
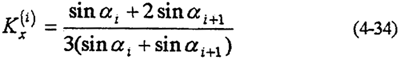
在計(jì)算中，接觸角φ的大小是預(yù)先給定的绵另，它的大小與接觸處的剛度悬鲜、間隙以及潤(rùn)滑情況等因素有關(guān)。一般情況下姨莽，在120°～180°范圍內(nèi)選取厉源，本文接觸角取φ=150°計(jì)算。
上一頁(yè)
下一頁(yè)
