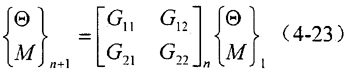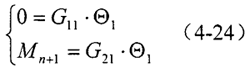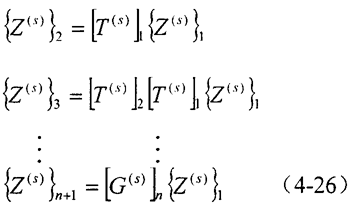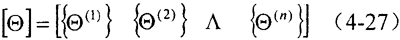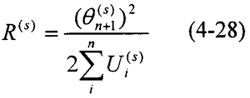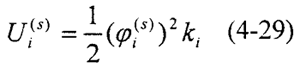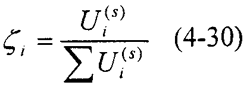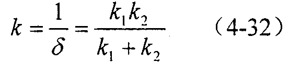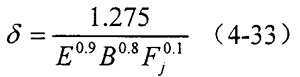|
4.4系統(tǒng)固有特性及勢(shì)能分布率
要分析和評(píng)價(jià)減速器的扭振特性匪煌,必須先計(jì)算出系統(tǒng)的各階固有頻率粟墩、相應(yīng)的主振型和各階模態(tài)柔度讨跟。
4.4.1固有頻率和主振型的確定
欲求系統(tǒng)的各階固有頻率和主振型山刨,需求解系統(tǒng)的無阻尼自由振動(dòng)方程岔冯。當(dāng)系統(tǒng)自由振動(dòng)時(shí)匾浪,激勵(lì)力矩和阻尼均為零椭吠,此時(shí)系統(tǒng)的數(shù)學(xué)模型以復(fù)數(shù)表示為:
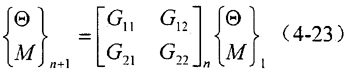
根據(jù)邊界條件,系統(tǒng)自由端狀態(tài)矢量中M=0梁促,固定端Θ=0修扁。代入式(4-23)得
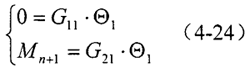
式(4-24)有非零解的充要條件是
G11=0 (4-25)
當(dāng)不計(jì)阻尼時(shí),慣性元件的傳遞矩陣是系統(tǒng)振動(dòng)頻率的平方ω2的函數(shù)榔况,彈性元件的傳遞矩陣僅與元件的剛度有關(guān),所以系統(tǒng)累積傳遞矩陣的元素G22是ω2的函數(shù)勃拢,并且ω2的階次與系統(tǒng)的慣性元件數(shù)目相同钩榄,所以滿足式(4-25)的振動(dòng)頻率均為系統(tǒng)的固有頻率。
求出系統(tǒng)的各階固有頻率ω后后涛,即可求出相應(yīng)各階主振型和系統(tǒng)主振型武也。倘若取第s階固有頻率ωs代入下式,便右逐一求出各元件的第s階狀態(tài)矢量Θ1(s)口愁、Θ2(s)耿逐、…、Θn+1(s)鸿挠。
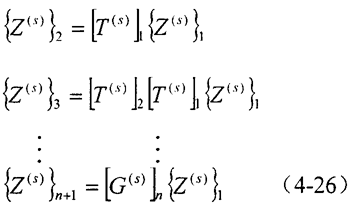
所取得的一系列Θ(s)值醇舶,便是第s階主振型{Θ(s)},它表示系統(tǒng)以ωs頻率扭振時(shí)宋梧,各慣性元件扭轉(zhuǎn)角大小的相對(duì)比值匣沼。將各階主振型向量合并即可得到系統(tǒng)的主振型。
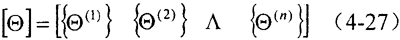
4.4.2 模態(tài)柔度和勢(shì)能分布率的確定
在建立了反映傳動(dòng)系統(tǒng)動(dòng)態(tài)特性的數(shù)學(xué)模型的基礎(chǔ)上捂龄,可對(duì)結(jié)構(gòu)進(jìn)行動(dòng)力修改或優(yōu)化設(shè)計(jì)以使所設(shè)計(jì)的系統(tǒng)具有良好的動(dòng)態(tài)特性释涛。通常的結(jié)構(gòu)動(dòng)力修改問題,是要求把結(jié)構(gòu)的振動(dòng)強(qiáng)度或動(dòng)柔度限制在一定的范圍內(nèi)倦沧。有效的修改過程是先找出結(jié)構(gòu)的薄弱環(huán)節(jié)唇撬,然后有針對(duì)性的修改薄弱環(huán)節(jié)的局部結(jié)構(gòu)它匕,從而使整個(gè)系統(tǒng)的動(dòng)態(tài)特性滿足要求。確定結(jié)構(gòu)薄弱環(huán)節(jié)并以此為依據(jù)進(jìn)行結(jié)構(gòu)修改的方法主要是考察系統(tǒng)的模態(tài)柔度和勢(shì)能分布率窖认。
由于系統(tǒng)的最大能量Emax是與振型向量{Θ}的平方成正比的豫柬,不論阻尼大小如何,這個(gè)比例關(guān)系總是一定的耀态。因此轮傍,模態(tài)柔度是一個(gè)與阻尼無關(guān)的參數(shù),其大小僅取決于系統(tǒng)的結(jié)構(gòu)參數(shù)和物理參數(shù)首装。改變結(jié)構(gòu)參數(shù)抱典、物理參數(shù)的大小和配置方式,均將使其發(fā)生明顯的變化赊偿。系統(tǒng)的第s階模態(tài)柔度R(s)的定義為
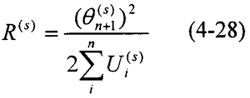
式中θn+1(s)——系統(tǒng)末端在第s階模態(tài)振動(dòng)時(shí)的扭振幅值(rad)绵另;
Ui(s)——系統(tǒng)中第i 個(gè)彈性元件在第s階模態(tài)振動(dòng)時(shí)的勢(shì)能。其值為
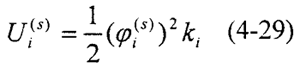
式中Ui(s)——系統(tǒng)中第i 個(gè)彈性元件在第s階模態(tài)振動(dòng)時(shí)的轉(zhuǎn)角绅鉴。
模態(tài)柔度的大小表明了該階模態(tài)的危險(xiǎn)程度姨莽。模態(tài)柔度越大,說明該階模態(tài)越危險(xiǎn)既蛙。但要找出造成該階模態(tài)危險(xiǎn)的原因仲侈,確定結(jié)構(gòu)修改的部位和修改內(nèi)容,僅憑模態(tài)柔度值還不夠蓖社,還必須考察各個(gè)彈性元件的勢(shì)能或勢(shì)能分布率秆惑。勢(shì)能分布率定義為
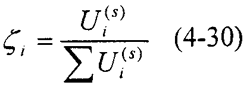
勢(shì)能分布率的大小表明系統(tǒng)中彈性元件變形能的大小,勢(shì)能分布率最大的元件也就是系統(tǒng)的最薄弱環(huán)節(jié)衍止,即造成該階模態(tài)危險(xiǎn)的主要原因哗蛋。據(jù)此可以確定相應(yīng)的改進(jìn)措施,以提高系統(tǒng)的動(dòng)態(tài)性能园担。
4.5 動(dòng)力學(xué)模型參數(shù)的確定
在滾柱活齒減速器扭振動(dòng)力學(xué)模型中届谈,其參數(shù)包括幾何參數(shù)、物理參數(shù)和外載荷參數(shù)三類弯汰。幾何參數(shù)在減速器系統(tǒng)設(shè)計(jì)完成后即己完全確定艰山,在物理參數(shù)中有質(zhì)量參數(shù)(如轉(zhuǎn)動(dòng)慣量)、剛度參數(shù)(如活齒副嚙合剛度蝙泼、傳動(dòng)軸扭轉(zhuǎn)剛度等)和阻尼參數(shù)(如軸類零件扭轉(zhuǎn)阻尼)程剥。其中,轉(zhuǎn)動(dòng)慣量在系統(tǒng)設(shè)計(jì)后即可計(jì)算求得汤踏,傳動(dòng)軸扭轉(zhuǎn)剛度可以按材料力學(xué)方法計(jì)算织鲸。下面給出活齒副嚙合剛度和軸類零件扭轉(zhuǎn)阻尼的計(jì)算方法。
4.5.1 活齒副的嚙合剛度
活齒副的嚙合剛度是指工作時(shí)活齒副共同抵抗變形的能力溪胶,它與嚙合副的綜合彈性變形有關(guān)搂擦。嚙合副的綜合彈性變形是指活齒副在嚙合過程中彈性變形的總和稳诚,表示為
δ=δ1+δ2 (4-31)
式中
δ1——活齒的彈性變形(mm);
δ2——波發(fā)生器瀑踢、活齒架或中心輪的彈性變形(mm)扳还。
活齒副嚙合剛度k可表示為:
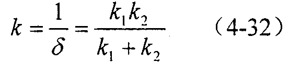
式中
k1——活齒的接觸剛度(N/mm),k1=1/δ1;
k2——波發(fā)生器咱茂、活齒架或中心輪的接觸剛度(N/mm),k2=1/δ2掰废。
只要求出活齒及與活齒嚙合件的接觸變形,即可確定嚙合綜合剛度缴碉。接觸變形的計(jì)算按下式進(jìn)行:
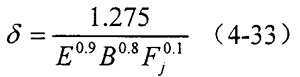
式中
E——材料彈性模量(N/mm2)敢添;
B——齒寬(mm);
4.5.2 軸類零件扭轉(zhuǎn)阻尼
軸類零件的扭轉(zhuǎn)阻尼主要是材料阻尼叁乍,根據(jù)H.H.Lin.和C.Lee.等的分析季训,其扭轉(zhuǎn)阻尼可利用下式進(jìn)行計(jì)算:

式中ks——軸類零件的扭轉(zhuǎn)剛度(N·mm/rad);
ξs——軸類零件的扭轉(zhuǎn)阻尼系數(shù)则沃,根據(jù)D.R.Houser等的試驗(yàn)研究肝庸,ξs一般取0.005~0.075;
I1,I2——分別為軸類零件兩端慣性元件的轉(zhuǎn)動(dòng)慣量(kg·mm2)章迎。
4.6 滾柱活齒減速器扭振動(dòng)態(tài)特性分析
利用前面建立的滾柱活齒減速器系統(tǒng)的動(dòng)力學(xué)模型對(duì)減速器系統(tǒng)進(jìn)行扭振分析吓死,找出系統(tǒng)的固有特性,即固有頻率和主振型焚寂。由于軸承的旋轉(zhuǎn)阻尼很小统岭,這里忽略不計(jì)。根據(jù)減速器各元件實(shí)際尺寸計(jì)算得到各慣性元件的等效轉(zhuǎn)動(dòng)慣量粉臊、彈性元件的等效扭轉(zhuǎn)剛度如表4-1所示。
表4-1慣性元件的等效轉(zhuǎn)動(dòng)慣量和彈性元件的等效扭轉(zhuǎn)剛度
| I1(kg·mm2) |
I2(kg·mm2) |
I3(kg·mm2) |
k1(N·mm/rad) |
k2(N·mm/rad) |
k3(N·mm/rad) |
| 2.2342×103 |
2.0833×104 |
7.2384×105 |
1.3313×1011 |
1.3313×1011 |
2.6864×1011 |
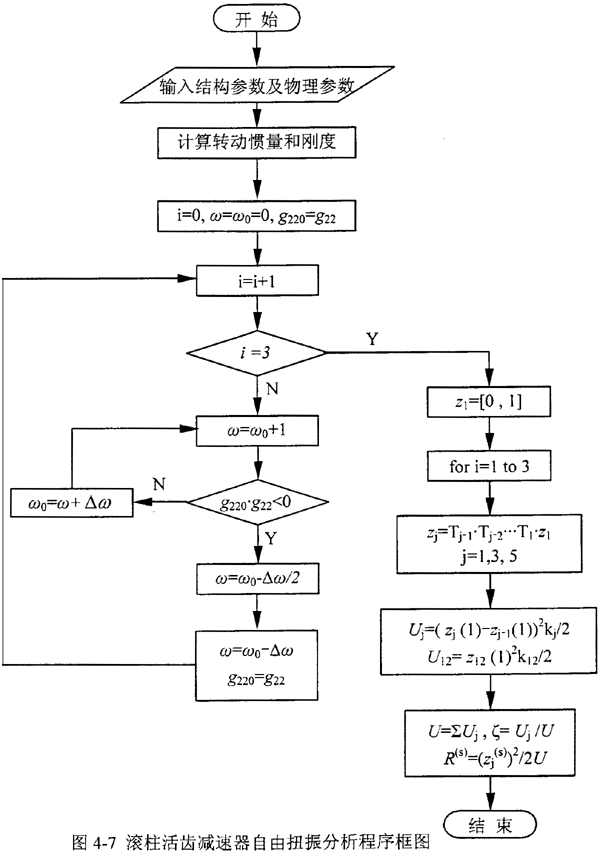
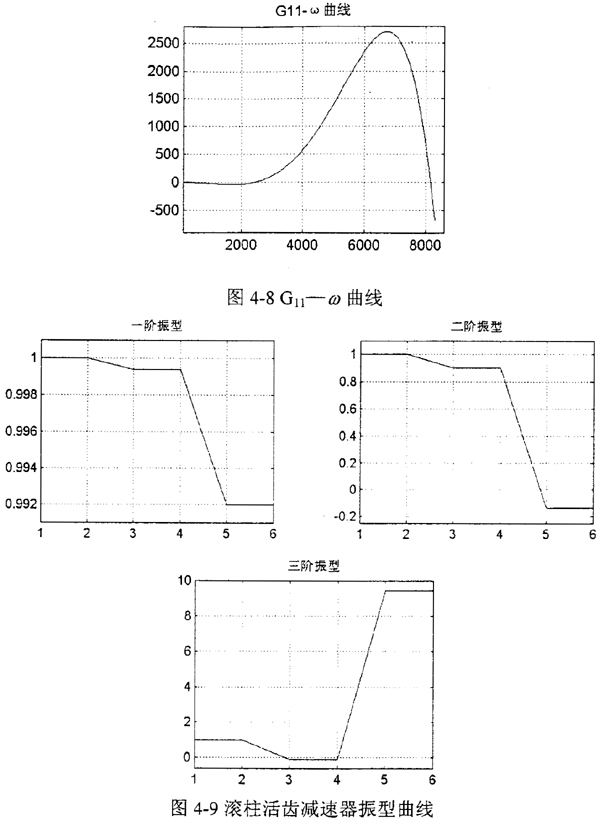
根據(jù)前面介紹的方法驶兜,在計(jì)算機(jī)上編程對(duì)減速器的扭振動(dòng)力學(xué)特性進(jìn)行分析扼仲,其程序框圖見圖4-7所示。在計(jì)算機(jī)上運(yùn)算時(shí)抄淑,按照確定的頻率步長對(duì)頻率方程掃頻屠凶,作出“G11-ω”曲線,如圖4-8所示肆资,凡G22=0時(shí)的ω值矗愧,就是系統(tǒng)的固有頻率。有關(guān)固有頻率郑原、勢(shì)能分布率和模態(tài)柔度的計(jì)算結(jié)果見表4-2唉韭。另外,利用該程序還繪制出圖4-9所示的減速器系統(tǒng)的振型曲線犯犁。
表4-2 滾柱活齒減速器扭振動(dòng)力學(xué)分析結(jié)果
| 固有頻率(×103rad/s) |
0.1896 |
2.4281 |
8.1645 |
| 主振型 |
{1.0000,0.9994,0.992} |
{1.0000,0.9011,-0.1358} |
{1.0000,-0.1186,9.4318} |
勢(shì)能分
布率 |
彈性元件1 |
0.4551 |
0.5508 |
0.0527 |
| 彈性元件2 |
0.4545 |
0.4472 |
0.00074227 |
| 彈性元件3 |
0.0904 |
0.0020 |
0.9465 |
| 系統(tǒng)模態(tài)柔度×10-7/rad(N·mm)-1 |
3.3637×10-5 |
7.6298×10-7 |
3.5234×10-4 |
通過表4-2中的分析結(jié)果我們可以看出属愤,三階(8.1645×103rad/s)系統(tǒng)模態(tài)柔度最大女器,所以該階模態(tài)是危險(xiǎn)模態(tài)。要找出造成該階危險(xiǎn)模態(tài)的具體原因岗命,我們可以考察各彈性元件的勢(shì)能分布率巨脚。從表4-2中可以看到,此時(shí)3號(hào)彈性元件的勢(shì)能分布率最大品救,這說明在扭轉(zhuǎn)時(shí)敢弟,它的彈性變形能最大,即它是最薄弱環(huán)節(jié)他景,是造成危險(xiǎn)模態(tài)的主要原因捅振。從這個(gè)結(jié)論出發(fā),便可以采取相應(yīng)措施來改進(jìn)設(shè)計(jì)方案式伶。通過適當(dāng)增加活齒架的壁厚或減小輸出軸長度來提高扭轉(zhuǎn)剛度呀琢,便可改善該減速器的動(dòng)態(tài)特性。動(dòng)態(tài)性能好的系統(tǒng)應(yīng)該是各階模態(tài)柔度小而且每階模態(tài)中各元件的能量分布均勻贡金。為了達(dá)到這個(gè)目標(biāo)壕归,可以按照上述方法繼續(xù)調(diào)整有關(guān)彈性元件的扭轉(zhuǎn)剛度,直到獲得滿意的結(jié)果為止衅侥。
在負(fù)載變化和誤差較小的情況下癞季,滾柱活齒減速器系統(tǒng)的激勵(lì)頻率就是嚙合剛度的變化頻率。它的計(jì)算如下:
ω=2πni/60i=34.7rad/s
式中ni——輸入軸轉(zhuǎn)速(rpm)倘潜;
i——傳動(dòng)比绷柒。
由表4-2中結(jié)果可知,減速器系統(tǒng)的一階基頻為189,6radis涮因,系統(tǒng)基頻遠(yuǎn)大于激勵(lì)頻率废睦,因此該減速器的振動(dòng)水平較低,振動(dòng)和噪聲較小养泡。
4.7 本章小結(jié)
1.通過將組成滾柱活齒減速器的各個(gè)零件簡化成相應(yīng)的慣性元件和彈性元件嗜湃,建立了減速器的系統(tǒng)動(dòng)力學(xué)模型;通過將各慣性元件和彈性元件轉(zhuǎn)換到輸入軸上澜掩,得到了適于用傳遞矩陣法進(jìn)行動(dòng)力學(xué)分析的鏈狀動(dòng)力學(xué)模型购披。
2.在建立起慣性元件和彈性元件動(dòng)力學(xué)數(shù)學(xué)模型的基礎(chǔ)上,利用傳遞矩陣法建立了減速器系統(tǒng)的動(dòng)力學(xué)數(shù)學(xué)模型肩榕;給出了活齒副嚙合剛度和軸類零件扭轉(zhuǎn)阻尼的計(jì)算公式刚陡。
3.利用所建立的動(dòng)力學(xué)模型,通過編程分析了井下驅(qū)動(dòng)螺桿泵采油減速器樣機(jī)的自由振動(dòng)株汉。得到了該系統(tǒng)的固有頻率筐乳、模態(tài)柔度和各階振型等動(dòng)態(tài)特性參數(shù)。結(jié)果表明,該減速器具有良好的動(dòng)態(tài)特性克酿。
4.根據(jù)所求的模態(tài)柔度和各彈性元件的勢(shì)能分布率颅唇,找到了危險(xiǎn)模態(tài)及導(dǎo)致危險(xiǎn)模態(tài)的薄弱環(huán)節(jié),為進(jìn)一步改進(jìn)其結(jié)構(gòu)限匕,提高動(dòng)態(tài)特性西练,提供了理論依據(jù)。
上一頁
下一頁
|