第五章 帶有非線性聯(lián)軸器軸系穩(wěn)態(tài)響應(yīng)計(jì)算方法的研究
5-1 帶有非線性聯(lián)軸器軸系力學(xué)和數(shù)學(xué)模型的建立
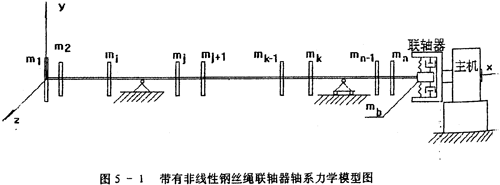
在第三章星立，根據(jù)試驗(yàn)的基礎(chǔ)建立了具有非線性遲滯特性聯(lián)軸器的恢復(fù)力模型乘碑。這一章彤悔，將研究一個(gè)帶有這種聯(lián)軸器的軸系如圖5-1所示萤榔，該軸系有n個(gè)圓盤，由鋼絲繩聯(lián)軸器與主機(jī)相連接诬忱，按以下原則建立力學(xué)模型：
1.每個(gè)圓盤均視為剛性勻質(zhì)骡侮，所有圓盤的質(zhì)量mi都有不同程度的偏心距ei。轉(zhuǎn)軸軸線垂直通過各圓盤的幾何中心忿奈；
2.設(shè)軸承辟瞄、軸承座以及聯(lián)軸器各向同性，靜坐標(biāo)系如圖5-1所示饰址，支座處理成簡(jiǎn)支坝给；
3.聯(lián)軸器從動(dòng)端處理成一集中質(zhì)量mb，由于聯(lián)軸器主動(dòng)端與主機(jī)軸相連接产舞，主機(jī)軸相對(duì)軸系軸來說魂奥，較短較粗，剛性較大易猫，變形較小耻煤，故將聯(lián)軸器主動(dòng)端、主機(jī)軸視為一體准颓，位移為零哈蝇，聯(lián)軸器從動(dòng)端與主動(dòng)端之間由非線性彈簧及非線性阻尼器聯(lián)結(jié)；
4.軸系為小位移振動(dòng)攘已，且忽略回轉(zhuǎn)效應(yīng)买鸽。
當(dāng)主機(jī)以角速度ω轉(zhuǎn)動(dòng)時(shí)，軸系在各偏心力的作用下產(chǎn)生穩(wěn)態(tài)振動(dòng)贯被，其運(yùn)動(dòng)微分方程可表示為：
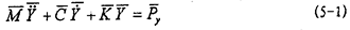
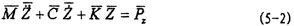
式中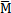
眼五，
，
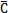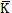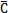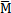彤灶，分別為軸系的質(zhì)量矩陣看幼、阻尼矩陣和剛度矩陣。其中阻尼矩陣=a+b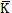鹿连，a缠染，b為比例常數(shù)。
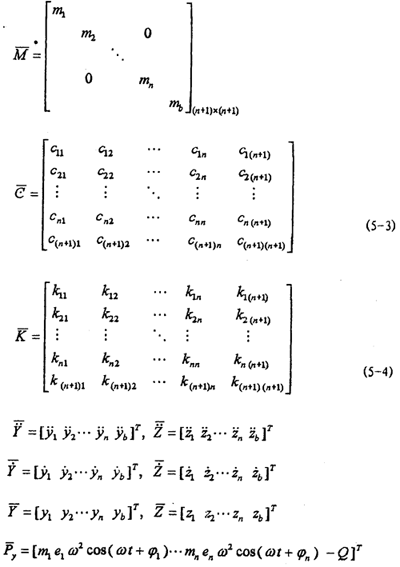
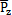=[m1e1ω2sin（ωt+
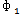）…mnenω2sin（ω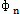t+
）
]T
其中：yi,zi分別為軸系中第i個(gè)圓盤在y,z方向的位移分量磷拧；
i=dyi/dt骡梨，
i=d2yi/dt2，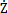
i=dzi/dt者赴，
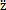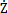b=d2zi/dt2分別為對(duì)應(yīng)于位移分量yi,zi的速度和加速度日胖，yb,zb為聯(lián)軸器從動(dòng)端集中質(zhì)量塊mb在y,z方向的位移瞎介；b=dyb/dt，b=d2yb/dt2习荚，b=dzb/dt融辈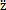，b=d2zb/dt2分別為對(duì)應(yīng)于位移分量yb,zb的速度和加速度；
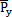仁娱，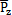
為y,z方向的激勵(lì)力向量胧蹲，其中mieiω2cos（ωt+
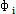），mieiω2sin（ωt+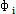）分別為y,z方向的偏心力分量囊祝；（
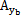殉酬，yb，b伞辛，ωt),（
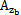黍檩，zb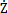，b始锚，ωt）分別為非線性彈性聯(lián)軸器恢復(fù)力在y,z方向的分量刽酱。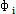為第i個(gè)圓盤質(zhì)量偏心的初相位角，即軸系靜止時(shí)瞧捌，第i個(gè)圓盤質(zhì)心和幾何中心連線與水平軸的夾角棵里。
由于假設(shè)軸承、軸承座以及聯(lián)軸器各向同性姐呐，式（5-1〕殿怜、式（5-2）解法相同，只需要討論二者之一即可曙砂。
式（5-l）表示一個(gè)局部非線性彈性和阻尼元件的振動(dòng)系統(tǒng)头谜，對(duì)這種系統(tǒng)，按現(xiàn)有常規(guī)方法來求解是非常困難的鸠澈，為此柱告，本文以GILM為基礎(chǔ)發(fā)展了一種稱為SSGILM(Separate System-Gal-erkin and Improved Levenbery-Marquar-dt）的方法來求解此類微分方程組。
5-2 SSGILM法
一.振動(dòng)微分方程組的改寫和解耦
首先把有局部非線性系統(tǒng)振動(dòng)微分方程組（5-1）式改寫成只有線性常系數(shù)的微分方程組和一個(gè)具有非線性變參數(shù)的微分方程兩部分：
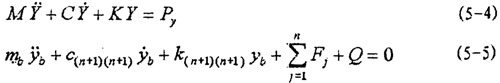
式中：
式（5-4）的Py中含有yb和b而（5-5）的Fj中含有yj颖助，j（j=1旋囤，2，… n）戏筹。這樣凯怕，軸系分成運(yùn)動(dòng)微分方程耦聯(lián)的兩個(gè)子系統(tǒng)—線性軸系子系統(tǒng)和非線性聯(lián)軸器子系統(tǒng)。
式（5-4）為線性方程缓万，按常規(guī)方法可求出無阻尼的各階固有頻率pi以及對(duì)應(yīng)的主振型Yi向量（i=1甩楷，2，…，n）催锯，Yi分別除以相應(yīng)廣義質(zhì)量的平方根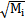
（Mi=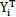
MYi）得到正則振型YNi向量滴练。引入正則振型坐標(biāo)WNi，對(duì)（5-4）式進(jìn)行坐標(biāo)變換欠诊；
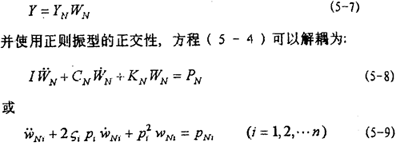
式中，WNi為正則振型向量WN中的第i個(gè)分量辟劲，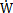
Ni和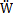
Ni臣疑，分別為它對(duì)時(shí)間t的一次導(dǎo)數(shù)和二次導(dǎo)數(shù)；I為單位矩陣徙菠；
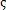i=（a+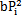
）/2Pi=cii2pimi為振型比例阻尼比讯沈；PNi為PN=
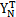Py激勵(lì)力向量中的第i個(gè)分量。
經(jīng)正則坐標(biāo)變換婿奔，雖然得到互不耦合的線性微分方程組（5-9)缺狠，但是（5-9）式仍然不能像單自由度振動(dòng)系統(tǒng)那樣求解，因?yàn)椋?-9）式中的激勵(lì)力包含未知的振動(dòng)位移yb和振動(dòng)速度b萍摊。如果yb已知挤茄，就可以從（5-9）式中解得WNi，進(jìn)而可以由（5-7）式得到各yi冰木。因此需要求得yb穷劈。
圖5-1所示軸系在主機(jī)帶動(dòng)下轉(zhuǎn)動(dòng)時(shí)，各圓盤質(zhì)量偏心將產(chǎn)生周期偏心激勵(lì)力踊沸，根據(jù)第二章的試驗(yàn)結(jié)果歇终，聯(lián)軸器非線性恢復(fù)力Q是時(shí)間的周期函數(shù)，因此當(dāng)軸系中有聯(lián)軸器這種局部非線性元件時(shí)逼龟，可以設(shè)它的位移響應(yīng)是周期性的评凝，即假設(shè)yb有下面的形式：
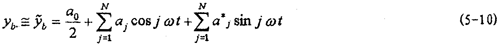
由式（5-6）、（5-8）和（5-9）可知秦代，激勵(lì)力由二類力構(gòu)成潦号，一類是質(zhì)量偏心力mieiω2cos（ωt+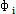），另一類是恢復(fù)力-ki（n+1）yb-ci（n+1）b蚯景，為求解（5-8）式方便昭怕，將（5-10）代入（5-8）式，并將正則激勵(lì)力分解成：
PN=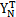Py=PN1+PN2 （5-11）
式中：
由（5-11）和（5-12）式可知服驼，若{a}已知裙都，就可以由（5-12）式求出各WNi，代WNi入（5-7）式鹅唠，可以得到各yi咽皮。由此可以把求yb的問題轉(zhuǎn)化為求{a}=[a0 a1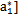 
T的問題。
上一頁(yè)
下一頁(yè)
