第5章 雙聯(lián)三叉桿式萬向聯(lián)軸器的動力仿真
5.1 引言
任何機械都有運動欣慰，任何機械都受到力的作用，各種機械因受到力的作用而運動纱扭，在運動中又會產(chǎn)生力衡怀。正是由于力和運動的相互影響棍矛，才使動力學問題相當?shù)膹碗s，這一點在空間機構中體現(xiàn)更是突出抛杨。由前面的分析可知够委，三叉桿式萬向聯(lián)軸器機構是一種運動規(guī)律非常復雜的空間機構，它的動力分析自然十分復雜怖现，如用手工去計算幾乎不可能茁帽。
動力分析是進行機械設計的基礎。只有通過動力分析知道物體的受力狀況屈嗤，才可在機械設計中對物體進行強度潘拨、剛度、疲勞饶号、壽命等機械性能進行計算铁追。由此，動力分析的重要性可見一斑对轴。
由于動力學研究的復雜性溺硼，人們常常引入一些假定，使問題簡化青竹。有時這種假定無關緊要触晃，有時則會導致計算的失誤冗吟。但隨著生產(chǎn)實踐的發(fā)展俱报，對動力學分析的準確度提出了新的要求。如果仍舊采用靜態(tài)代替動態(tài)的靜力學方法和恒定動態(tài)代替變動動態(tài)的動態(tài)靜力學方法演侍，則根本不能滿足分析的要求哼狰。為此必須進行真正的動力學分析或彈性動力學分析。
力學理論的發(fā)展色递、電子計算機的改進和廣泛應用為動力學分析方法提供了理論基礎和實踐手段痊追。目前在眾多的CAD、CAE軟件中粪趋，ADAMS以其較強的運動學蛆狱，動力學分析功能在眾多工程領域里獲得了廣泛的應用，利用它能較好的解決上述的動力學問題磺浙。
本章利用ADAMS軟件洪囤，對第四章中建立的雙聯(lián)三叉桿萬向聯(lián)軸器進行多剛體的動力分析，得到了一些有用的撕氧、可視化的結果瘤缩。
5.2 理論背景
5.2.1 機械動力學簡介
機械動力學研究機械在力作用下的運動和在運動中產(chǎn)生力的科學喇完。由于機械產(chǎn)品的高速化、精密化剥啤、輕量化锦溪、大功率化的發(fā)展趨向不斷促使機械動力學的發(fā)展，要求提出更精確府怯、更真實的反映客觀實際的動力學分析方法而摒棄以前在計算中的許多假設和簡化刻诊。
在機械動力學發(fā)展的過程中產(chǎn)生了如下四種分析方法：
靜力學分析（Static Analysis）。對于低速機械牺丙，在運動中的慣性力可以忽略不計坏逢。在機械運動過程中的各個位置采用靜力平衡的方法求解；
動態(tài)靜力學分析（Kineto-Static Analysis）赘被。隨著機械的速度的提高是整，慣性力不能再被忽略。假定構件按理想的規(guī)律運動砍篇，利用達朗貝爾原理求解以叛；
動力學分析（Dynalnic Analysis）。由于在各種力的作用下笛蛋，機械并不能維持理想的運動規(guī)律這一假定疼喝，在分析中，把原動機包括在機械系統(tǒng)之內(nèi)來進行分析绢拓。
彈性動力學分析（Elasto-dynamics Analysis）我值。在前三種分析方法中，構件均被假定為剛性的然怕，但隨著機械輕量化的發(fā)展岸零，構件柔性加大，運轉速度提高鱼灶，慣性急劇增大竞蹲，在這種情況下，構件的彈性變形會給機械運動的輸出帶來誤差信高。
機械彈性動力學是機械動力學發(fā)展的新階段闸衫，它研究把機械的構件看作是彈性的而不是剛性時的機械運動狀態(tài)，以及為抑制彈性動力響應而采取的措施和相應的機械設計方法诽嘉。目前這種方法已得到了廣泛的應用蔚出。
5.2.2 ADAMS中的動力學方程
ADAMS中采用拉格朗日乘子法建立系統(tǒng)動力方程
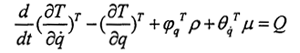
完整約束方程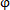
（q，t）=0
非完整約束方程θ(q虫腋，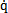
骄酗，t)=0
其中：
T——系統(tǒng)動能；
q——系統(tǒng)廣義坐標列陣；
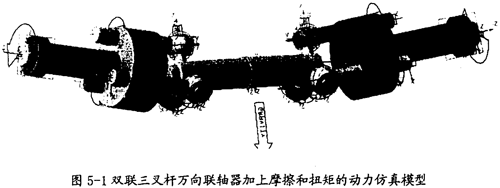
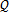——廣義力列陣酥筝；
p——對應于完整約束的拉氏乘子列陣滚躯；
μ——對應于非完整約束的拉氏乘子列陣；
通過求解此微分方程的數(shù)值解嘿歌，即可得到結果掸掏。
5.3 雙聯(lián)三叉桿式萬向聯(lián)軸器的動力仿真
5.3.1 分析模型的建立
本分析模型是在第四章中的運動分析模型（圖4-18）的基礎上通過除去運動驅動，加上驅動力宙帝、摩擦力而得到圖5-1所示的動力仿真模型丧凤。
目前在三叉桿式萬向聯(lián)軸器動力分析方面，所發(fā)表的論文大多是在忽略摩擦力與慣性力的條件下進行的步脓，僅是作最基礎的靜力學分析晰奉，或是考慮到恒定摩擦和慣性力的動態(tài)靜力學分析。而在實際應用中空崇，摩擦不僅是聯(lián)軸器實際失效的主要原因之一措抒，而且是影響效率的主要因素，另外在聯(lián)軸器高速運轉中慣性力是不可忽略的重要因素居绸。因此本章在考慮到摩擦和慣性力的情況下精克，進行真正的動力學分析（多剛體系統(tǒng)），必定會得出全新的結果因登，為這種聯(lián)軸器的進一步研究硅魁、開發(fā)打下基礎。
5.3.1.1 建立模型的的關鍵點
5.3.1.1.1 摩擦力的施加
在雙聯(lián)三叉桿式萬向聯(lián)軸器的模型中步鸣，相互運動的構件較多枯昂，各個構件之間的活動接觸面都會產(chǎn)生摩擦力的作用，不同的運動副形式醒囊，摩擦產(chǎn)生的來源也不一樣霸瘾，在施加摩擦時要根據(jù)不同的摩擦來源考慮各因素的影響。在本章的分析中弹惦，各個運動副間都被加上了摩擦力否淤。由于涉及到了如下四種運動副悄但，現(xiàn)對它們摩擦力施加的考慮因素作如下的陳述：
移動副：
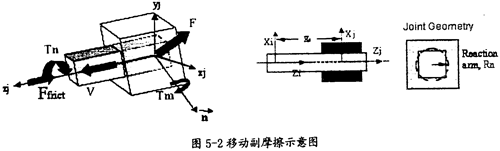
移動副產(chǎn)生摩擦的示意圖如圖5-2所示棠隐。在這種運動副中只會產(chǎn)生逆向于移動方向v（如圖5-2中藍色箭頭所示）的摩擦力Ffrict（如圖5-2中紅色箭頭所示）,它的產(chǎn)生主要由三種因素，即構件間相互作用的徑向力F檐嚣、構件間相互作用的扭矩Tn助泽、構件間相互作用的彎矩Tm（這三種力如圖5-2中綠色箭頭所示）。在施加由這些作用力產(chǎn)生的摩擦力時嚎京，要考慮徑向力F的大小嗡贺、等效作用臂長Rn（如圖5-2中右邊圖所示運動副間的重疊量和重疊量的變化情況、扭矩Tn的大小和它的等效反作用臂長Rn、彎矩Tm的大小和彎矩的反作用臂長XS（如圖5-2中間圖所示）诫睬。另外還得考慮靜摩擦系數(shù)煞茫、動摩擦系數(shù)及預載荷的作用。
圓柱副：
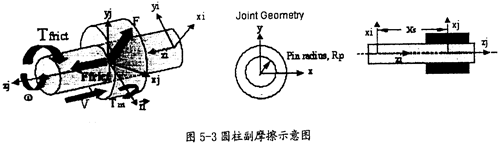
圓柱副產(chǎn)生摩擦的示意圖5-3所示摄凡。在這種動動副中會產(chǎn)生逆向于移動方向V（如圖5-3中藍色箭頭所示）的摩擦力Ffrict（如圖5-3中紅色箭頭所示）及逆向于旋轉方向ω（如圖5-3中藍色箭頭所示）的摩擦扭矩Tfnct（如圖5-3中紅色箭頭所示）续徽，它的產(chǎn)生主要由兩種因素，即構件間相互作用的徑向力F蘑慕、構件間相互作用的彎矩Tm（這兩種力如圖5-3中綠色箭頭所示）袒忿。在施加這些作用力產(chǎn)生的摩擦力時，要考慮徑向力F的大小蕊欣、圓柱半徑RP（如圖5-3中間圖所示）蓖桅、運動副間的重疊量和重疊量的變化情況、彎矩Tm的大小和彎矩的反作用臂長Xs（如圖5-2中右圖所示）愈秕，另外還得考慮靜摩擦系數(shù)舍稽、動摩擦系數(shù)及預載荷的作用。
旋轉副：
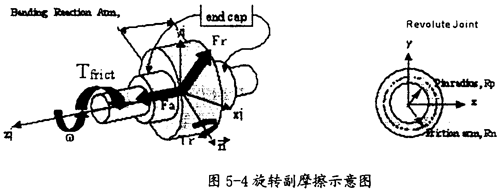
旋轉副產(chǎn)生摩擦的示意圖如圖5-4所示言盼。在這種運動副中只會產(chǎn)生逆向于旋轉方向ω（如圖5-4中藍色箭頭所示）的摩擦扭矩Tfrict（如圖5-4中紅色箭頭所示）劫丧，它的產(chǎn)生主要由三種因素，即構件間相互作用的徑向力Fr蛀家、構件間相互作用的軸向力Fa浊待、構件間相互作用的彎矩Tr（這三種力如圖5-4中綠色箭頭所示）。在施加由這些作用力產(chǎn)生的摩擦力時馅溉，要考慮徑向力Fr的大小缔类、圓柱半徑RP（如圖5-4右圖所示）、軸向力Fα的大小劲阎、摩擦半徑Rn的大谢婷恕（如圖5-4右圖所示）、彎矩Tm的大小和彎矩的反作用臂長（即旋轉副的長度悯仙，如圖5-4中左圖所示）龄毡，另外還得考慮靜摩擦系、動摩擦系數(shù)及預載荷的作用锡垄。
球面副：
球面副產(chǎn)生摩擦的示意圖如圖5-5所示沦零。在這種運動副中只會產(chǎn)生逆向于旋轉方向的摩擦扭矩Tfrc（如圖5-5中紅色箭頭所示），它的產(chǎn)生只有一種因素货岭，即構件間相互作用的徑向力F（如圖5-5中灰色箭頭所示）路操。在施加由相互作用的徑向力F產(chǎn)生的摩擦力時，要考慮徑向力F的大小和球半徑千贯，另外還得考慮靜摩擦系數(shù)屯仗、動摩擦索數(shù)及預載荷的作用搞坝。
在這一過程中分別對20個運動副添加了摩擦力，這些力在仿真中將會隨著它們的產(chǎn)生因素的變化而變化魁袜。這在后面的結果中可以見到桩撮。
5.3.1.1.2 驅動力的施加
在動力仿真中，對微分方程的求解用的都是用數(shù)值計算的方法筛毡，在迭代求解的過程中坟荤，步長不可過長，如果步長太大饼尾，則在數(shù)值計算中會不收斂挽沧，導致仿真的失敗。在動力仿真中谐昌，如果規(guī)定了時間步的步長糙官，又添加了過大的驅動力，則在仿真中物體在較短的時間內(nèi)會發(fā)生很大的空間位移筒啄，在這種情況下鱼催，數(shù)值計算將很可能不收斂．故在進行動力仿真中，應讓整個變化過程平緩的進行贤方，仿止出現(xiàn)上述的現(xiàn)象见毒。
在ADAMS中提供了階梯函數(shù)（STEP函數(shù)），它可以作為解決這一問題的工具献甘。STEP函數(shù)簡述如下：
在ADAMS中吴攒，STEP函數(shù)近似一個標準的數(shù)學STEP函數(shù)（沒有不連續(xù)性）,并逐步逼近數(shù)值，例如：驅動或者力砂蔽，向上或者向下或者打開和關閉洼怔。它的函數(shù)圖形如圖5-6所示。格式同各參數(shù)說明如下：
格式：STEP(x,x0,h0,xl,hl)
參數(shù)說明：
x一自變量左驾，可以是時間或時間的任一函數(shù)倡鲸；
x0一自變量的STEP函數(shù)開始值占遥，可以是常數(shù)或函數(shù)表達式或設計變量；
x1一自變量的STEP函數(shù)結束值梢翼，可以是常數(shù)诸痢、函數(shù)表達式或設計變量匀洪；
h0一STEP函數(shù)的初始值展运，可以是常數(shù)播掷、設計變量或其它函數(shù)表達式；
h1一STEP函數(shù)的最終值桅锄，可以是常數(shù)琉雳、設計變量或其它函數(shù)表達式；
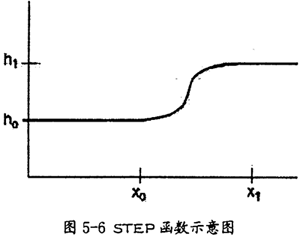
從以上說明中友瘤，可以知道翠肘，STEP函數(shù)能使數(shù)值之間的過度平緩。在本次仿真中正是利用了這一點虏向，在施加驅動力時采用了此函數(shù)档广，讓驅動力從O平緩過度到一個較大的值，使仿真平穩(wěn)地進行皇腮，避免了發(fā)散現(xiàn)象悄针。
在這一過程中分別在輸入軸同支承間的旋轉副及輸出軸同支承間的旋轉副上添加了STEP函數(shù)力矩驅動（輸出軸同支承間的旋轉副上的驅動作為負載，輸入軸同支承間的旋轉副上的驅動作為主動力矩）据值。
上一頁
下一頁
