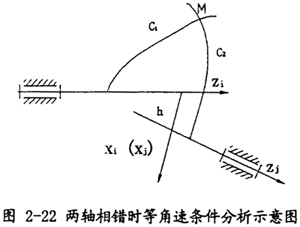
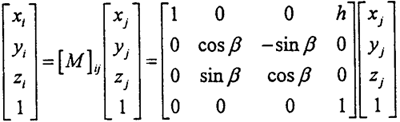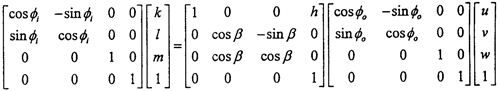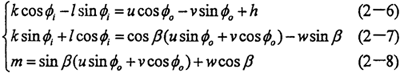2.3.2.1.2 輸入軸默徘、輸出軸相錯(cuò)時(shí)的同步性研究
假設(shè)兩軸的位置如圖2-22所示势嫁，建立模型及坐標(biāo)系如下：Zi和Zj分別為輸入軸男枝、輸出軸蔼邓，設(shè)Xi（Xj）與Zi和Zj的公垂線重合掏绍，h為兩軸間的最短距離褐澎，兩軸夾角為β岩臣。
進(jìn)行坐標(biāo)變換，則坐標(biāo)系OXjYjZj中的某點(diǎn)在OXiYiZi坐標(biāo)系中的坐標(biāo)可表示為：
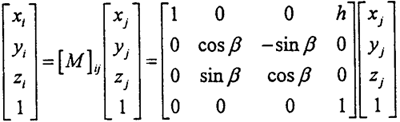
在此表示坐標(biāo)系變換矩陣向臀，兩軸嚙合點(diǎn)M的坐標(biāo)可如下求得：
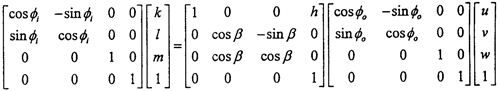
此處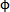
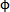i巢墅、0分別表示輸入軸、輸出軸在任意時(shí)刻轉(zhuǎn)過(guò)的任意角度隆文，由上式我們可導(dǎo)出以下的關(guān)系式：
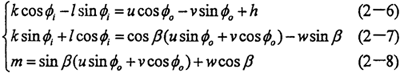
假設(shè)此時(shí)兩軸能夠?qū)崿F(xiàn)同步美卒，令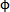i=0，則上式只有兩個(gè)未知量韧践，通過(guò)計(jì)算轿战，則可以導(dǎo)出兩軸運(yùn)動(dòng)的輪廓曲線存在著某種關(guān)系。
設(shè)（2-6）恒成立随象，通過(guò)比較兩端的系數(shù)可得：k=u载蜓，l=v，h=0
這顯然與已知不符聪蔬，因?yàn)閔≠0肄绢，可見(jiàn)假設(shè)不成立。
若再設(shè)（2-8）式恒成立无价，則有m=0,u=O,w=0,v=O详毡。代入（2-7）式中可得k=l=0，顯然這個(gè)結(jié)果是毫無(wú)意義的觅冈，因此假設(shè)不成立反璃。
通過(guò)以上的分析昵慌，我們知道假夺，兩軸相錯(cuò)時(shí)，在這種模型下斋攀，單一的萬(wàn)向聯(lián)軸器聯(lián)接不能實(shí)現(xiàn)同步的目的已卷。
2.3.2.1.3 定心式等角速萬(wàn)向聯(lián)軸器理論總結(jié)
定心式是指兩軸相交時(shí)的情況，盡管上述證明過(guò)程涉及到了兩軸相錯(cuò)時(shí)的等角速條件證明淳蔼，但未得出任何結(jié)果侧蘸，這里實(shí)際上只有定心式的等角速理論得到了證明。在證明中用到的模型傳力點(diǎn)只有一個(gè)鹉梨，這就是說(shuō)結(jié)論的得到是建立在聯(lián)軸器機(jī)構(gòu)模型中中間構(gòu)件只有一個(gè)的情況讳癌，多于一個(gè)的情況此結(jié)論就不一定正確了穿稳，因此這也限制了這一理論的應(yīng)用范圍。
2.3.2.2 定心式等角速萬(wàn)向聯(lián)軸器的產(chǎn)品
下面的兩類萬(wàn)向聯(lián)軸器在結(jié)構(gòu)上輸入軸和輸出軸始終相交于一點(diǎn)晌坤，只通過(guò)鋼球來(lái)傳遞力逢艘，是典型的定心式等角速理論的應(yīng)用。
2.3.2.2.1 球籠式萬(wàn)向聯(lián)軸器
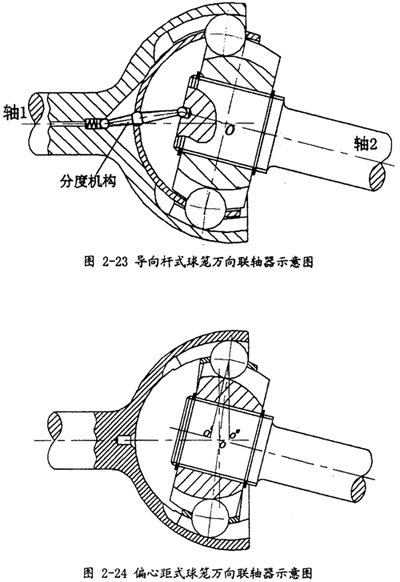
球籠式萬(wàn)向聯(lián)軸器是目前性能最優(yōu)良骤菠，應(yīng)用最廣泛的一種等角速萬(wàn)向聯(lián)軸器它改，根據(jù)結(jié)構(gòu)形式的不同可分為兩大類，即導(dǎo)向桿式球籠萬(wàn)向聯(lián)軸器和偏心距式球籠萬(wàn)向聯(lián)軸器刃傻，分別如圖2-23和圖2-24所示引苇。
導(dǎo)向桿式球籠萬(wàn)向聯(lián)軸內(nèi)外環(huán)上鋼球滾道溝槽的圓弧中心和保持架內(nèi)外球面的球心均重合確保萬(wàn)向節(jié)的中心o保持不變，如圖2-23所示鸣谒。當(dāng)兩軸線有相對(duì)的角位移時(shí)牌鹊，通過(guò)導(dǎo)向桿的作用能使鋼球分布在兩軸軸線相對(duì)角位移的等分角平面上，從而保證兩軸同步沟奸。導(dǎo)向桿式球籠萬(wàn)向聯(lián)軸器因零件數(shù)量較多飒迅、安裝不便，在應(yīng)用上受到了一定的限制懊玖。
偏心距式球籠萬(wàn)向聯(lián)軸器內(nèi)外環(huán)上鋼球滾道溝槽的圓弧中心o′和o″以相同偏心距分別置于對(duì)稱線（如圖2-24中藍(lán)色點(diǎn)劃線所示）的兩側(cè)泌弧，當(dāng)兩軸線有相對(duì)的角位移時(shí)，能使鋼球分布在兩軸軸線相對(duì)角位移的等分角平面上力鹰，從而保證兩軸同步翻框。
球籠式萬(wàn)向聯(lián)軸器的特點(diǎn)：同步性高、角位移大腺首、結(jié)構(gòu)簡(jiǎn)單信粮、體積小等許多優(yōu)點(diǎn)。已形成系列趁啸，并廣泛應(yīng)用于汽車强缘、冶金、輕工不傅、重型機(jī)械等部門旅掂。
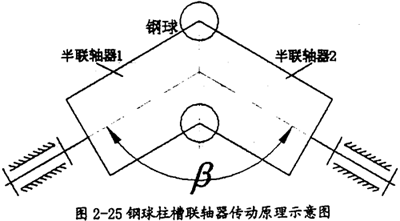
2.3.2.2.2 鋼球柱槽聯(lián)軸器
鋼球柱槽聯(lián)軸器同球籠式萬(wàn)向聯(lián)軸器一樣，它也通過(guò)鋼球來(lái)傳遞兩個(gè)半聯(lián)軸器之間的力访娶，當(dāng)兩個(gè)半聯(lián)軸器的軸線有相對(duì)的角位移時(shí)商虐，半聯(lián)軸器上的滾道能使鋼球分布在兩軸軸線相對(duì)角位移的等分角平面上（如圖2-25所示），從而保證兩軸同步崖疤。同球籠式萬(wàn)向聯(lián)軸器不同的是它的鋼球分布在一個(gè)橢圓面上秘车，而球籠式萬(wàn)向聯(lián)軸器則分布在一個(gè)球面上。
鋼球柱槽聯(lián)軸器是一種結(jié)構(gòu)極為簡(jiǎn)單且易于制造的等速聯(lián)軸器，因而具有實(shí)用價(jià)值叮趴，不過(guò)由于結(jié)構(gòu)上的限制這種聯(lián)軸器兩軸間的偏轉(zhuǎn)角較小割笙。
2.3.3 非定心式等角速萬(wàn)向聯(lián)軸器理論及其產(chǎn)品
2.3.3.1 非定心式等角速萬(wàn)向聯(lián)軸器傳動(dòng)理論
非定心式等角速理論：
輸入軸和輸出軸的相對(duì)轉(zhuǎn)動(dòng)瞬時(shí)轉(zhuǎn)軸或瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸位于或平行于兩軸的等分角平面。
理論證明如下：
2.3.3.1.1 單聯(lián)萬(wàn)向聯(lián)軸器等角速傳動(dòng)的必要條件
設(shè)單聯(lián)萬(wàn)向聯(lián)軸器的角速度為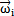
丰躺，輸出軸與輸入軸的瞬時(shí)角速度相等溅蓖，其角速度用
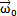來(lái)表示，兩軸線相交于0點(diǎn)攘调，偏轉(zhuǎn)角β隨時(shí)間的偏轉(zhuǎn)角速度為
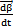剥讼。對(duì)此聯(lián)軸器可作出圖2-26所示的轉(zhuǎn)動(dòng)關(guān)系示意圖。
假設(shè)給整個(gè)系統(tǒng)加上一個(gè)角速度-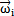拾哈，則根據(jù)理論力學(xué)中的知識(shí)可知輸出軸和輸入軸的關(guān)系仍保持不變乞芳，這時(shí)輸入軸的角速度變?yōu)榱悖斎胼S的運(yùn)動(dòng)可由下面的方法來(lái)分析染痊。
如圖2-26所示细抠，使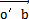
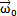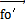矢量等于，
矢量等于-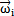组救，且∠bo′f=β喧丛，作
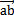平行于-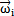，其大小等于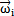辰车，則△abo′為等腰三角形缔直，由b點(diǎn)作
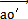的垂線，得垂足g博其，
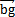垂線將△abo′等分成兩個(gè)直角三角形套才，這兩個(gè)直角三角形與△aco′為相似三角形。
由于： ∠ao′z′=
-
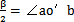
所以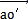
位于兩軸的等分角平面內(nèi)慕淡，因此-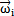和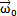的合成矢量即輸出軸相對(duì)于輸入軸的角速度
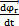也位于兩軸的等分角平面內(nèi)背伴。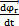的大小可通過(guò)△o′gb和△ogb來(lái)計(jì)算：
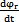=2ω0sin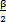
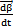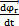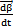由于矢量與輸入和輸出軸的軸線垂直，所以與的合成矢量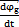
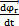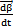=+也位于兩軸的等分角平面內(nèi)峰髓。合成矢量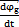的位置就是瞬時(shí)轉(zhuǎn)軸的位置傻寂。
所以軸線相交的等角速萬(wàn)向聯(lián)軸器輸出軸相對(duì)于輸入軸的相對(duì)轉(zhuǎn)動(dòng)瞬時(shí)轉(zhuǎn)軸始終位于兩軸的等分角平面內(nèi)⌒考慮到萬(wàn)向聯(lián)軸器的一般情形：輸入軸與輸出軸軸線并不位于同一平面內(nèi)疾掰，存在與輸入軸線和輸出軸線垂直的徑向位移，且有徑向移動(dòng)速度和軸向移動(dòng)速度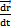
與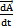
眉孩，如圖2-27所示个绍。
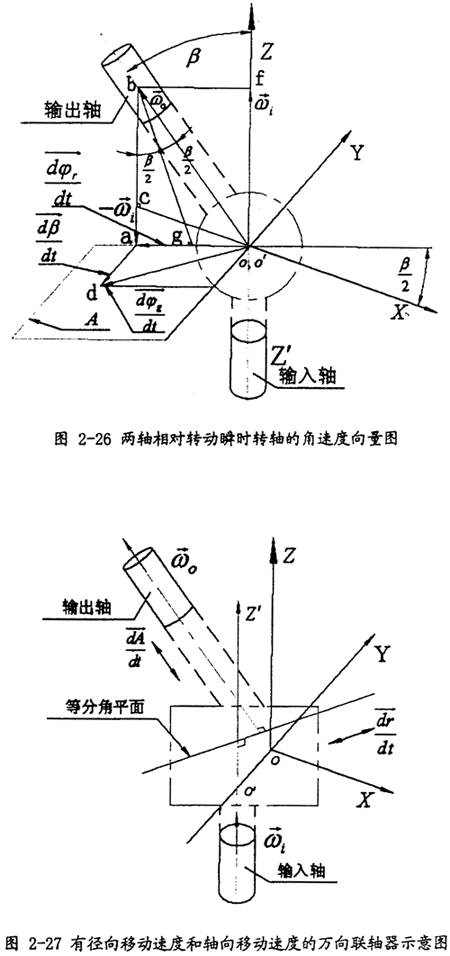
這些移動(dòng)速度不影響角速度矢量合成，即不影響瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的方位浪汪，但是對(duì)角速度所確定的瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的位置有一定影響，這時(shí)輸出軸相對(duì)于輸入軸的瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸不是位于而是平行于兩軸的等分角平面凛虽。這一結(jié)果是以兩軸角速度大小相等為前提條件推導(dǎo)出來(lái)的书吗，可以作為單聯(lián)萬(wàn)向聯(lián)軸器的普遍條件來(lái)應(yīng)用栓属，現(xiàn)將此條件簡(jiǎn)述如下：
具有等速傳動(dòng)特性的單聯(lián)萬(wàn)向聯(lián)軸器的必要條件為兩軸的相對(duì)轉(zhuǎn)動(dòng)瞬時(shí)轉(zhuǎn)軸或瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸位于或平行于兩軸的等分角平面。
上一頁(yè)
下一頁(yè)
