三環(huán)減速器建模及動態(tài)特性有限元分析計算
§3-1 引言
對三環(huán)減速器振動系統(tǒng)進行振動與噪聲的分析與研究寸宏,首先必須建立其數(shù)學模型辣铡,數(shù)學模型有理論建模和試驗建模兩類辕芳。所謂的理論建模是指由結構、機械的設計圖紙出發(fā)们豌,作出必要的假定與簡化涯捻,根據(jù)力學原理建模;而試驗建模是對振動系統(tǒng)進行激振玛痊,通過沒量獲得系統(tǒng)的輸入汰瘫、輸出數(shù)據(jù)狂打,再經(jīng)過對它們的分析擂煞、處理而建立的模型。這兩類方法各有其特點趴乡,可分別適用于自己特點的情況对省。在此,我們僅討論對三環(huán)減速器振動系統(tǒng)進行理論建模晾捏,并在SUN工作站上用I-DEAS軟件的有限元模塊及實體建模模塊對SHQ40建模并計算蒿涎,而試驗建模我們將在第六章中討論。
§3-2 描述振動系統(tǒng)的方法
振動系統(tǒng)有確定性和隨機系統(tǒng)兩大類惦辛,在這里劳秋,我們主要討論確定性振動系統(tǒng)。確定性振動系統(tǒng)通常分為分布參數(shù)振動系統(tǒng)和離散振動兩大類胖齐,不同的振動系統(tǒng)存在其相應的描述方法玻淑。
§3-2.1 分布能數(shù)振動系統(tǒng)
具有分布質(zhì)量、彈性和阻尼的系統(tǒng)茎冒,稱為分布參數(shù)或連續(xù)參數(shù)系統(tǒng)宫氛。在域D的每一點都應滿足如下的運動微分方程吆律。
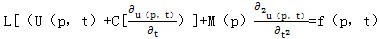
(3.1)
式中:U(p,t)——任意點p的位移间渐,它應滿足的邊界條件是:
B妈务,[u(p,t)]=0东哀,(i=0钓宗,1,2……尘斧,p)次瓣;
L—一個線性的2P階齊次數(shù)微分算子,它描述了系統(tǒng)的剛度分布星自;
C—一個類似于算子L的2P階線性齊次數(shù)分算子憾擒,它描述了系統(tǒng)的阻尼分布;
M—線性齊次微分算子塑崖,它描述了系統(tǒng)的質(zhì)量分布七冲;
f(p,t)——分布激振力规婆;
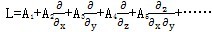
A
1澜躺,A
2……——坐標x,y抒蚜,z的函數(shù)掘鄙;
x,y嗡髓,z——p點的坐標操漠,即p(x,y饿这,z)浊伙;
B1——線性齊次微分算子;
由式(3.1)可知长捧,分布參數(shù)系統(tǒng)的運動是以偏微分方程來描述的嚣鄙,這類運動方程中所包含的參數(shù),通常是空間變量的連續(xù)函數(shù)秩纹。分布參數(shù)系統(tǒng)具有無限多個自由度幔时。所以,與一個分布參數(shù)系統(tǒng)相對應的特征解是由可數(shù)的然而是無限多個特征值和特征向量組成园撵。
為了獲得可靠的茉油、精確的分布參系統(tǒng)的數(shù)學模型,就需精確地確定運動方程中的各個參數(shù)。為此胸牲,利用如上述的試驗建模方法——振動參數(shù)識別技術是一個有效的方法蒸咏。通常,分布參數(shù)振動系統(tǒng)的參數(shù)識別方法有:(1)將分布參數(shù)系統(tǒng)離散化蝉蛙,獲得離散系統(tǒng)的模型悬坎,然后識別離散模型中的參數(shù)或與它相應的特征解;(2)直接以從布參數(shù)系統(tǒng)的響應識別分布參數(shù)系統(tǒng)運動微分方程中的各參數(shù)傅笨;(3)首先識別與實際分布參數(shù)系統(tǒng)相應的離散模型的特征解伸义,然后,利用識別的特征解來識別方程中的各個參數(shù)篮啦。
一個分布參數(shù)系統(tǒng)有無限多個的特征值與特征的向量胯恤。但是,人們不可能識別完全的特征解绰姻,通常是識別與該系統(tǒng)相應的低階特征值和特征向量枉侧。此外,目前的技術水平還不能滿足分布式測量的要求狂芋,因此榨馁,其識別工作還得借助于離散式測量來完成。
§3-2.2 離散振動系統(tǒng)
分布參數(shù)系統(tǒng)是一個非常復雜的系統(tǒng)帜矾,它給振動分析和振動參數(shù)識別帶來了很大困難翼虫,主要表現(xiàn)在:(1)系統(tǒng)的慣性、彈性屡萤、阻尼珍剑、激勵力和運動都依賴于空間坐標,因而導致數(shù)學上較難處理的偏微分方程及復雜的邊界條件死陆。因此招拙,一般情況下,除了少量的簡單結構外翔曲,很難獲得嚴格的封閉形式的解迫像;(2)不可能獲得分布的響應測量及無限多個特征解。因而误即,實際作振動分析、振動參數(shù)識別時牌君,通常將無限多個自由度的分布參數(shù)系統(tǒng)離散為有限自由度的離散振動系統(tǒng)捅腋。把分布參數(shù)系統(tǒng)離散化一般有以下幾種方法:
一、集中質(zhì)量法
把結構的質(zhì)量分別集中在若干點而形成有限個質(zhì)點的集中參數(shù)系統(tǒng)截剩。質(zhì)量元件绊寞、彈性元件和阻尼元件分別只有慣性、彈性和阻尼特性;
二条赚、廣義坐標法
把結構的變形分解為一系列具有固定形式的函數(shù)焰箩,而以廣義坐標表示結構的變形。這種方法递思,雖然理論上需要考慮無限多項影晋,但實際上只要考慮有限幾項即可獲得具有足夠精度的計算結果。如瑞利—里茲法毕删、模態(tài)坐標法等镜会。
三、有限元法
可以哈密頓原理導出的拉格朗日方程终抽,導出離散振動系統(tǒng)的一般運動微分方程式:
1.無源系統(tǒng)運動微分方程:
a.粘性阻尼系統(tǒng)運動微分方程:
M

+(C

+Kx=f(t) (3.3)
b.結構阻尼系統(tǒng)運動微分方程:
M

+(K+jD)x=

(3.4)
c.保守系統(tǒng)運動微分方程:
M

+Kx=f(t) (3.5)
2.有源系統(tǒng)運動微分方程:
M

+(G+C)

+(K+H)X=f(t) (3.6)
上式中:M——質(zhì)量矩陣戳表,正定矩陣;
C——粘性阻尼矩陣昼伴,實對稱正定式或半正定短陣匾旭;
D——結構阻尼矩陣,實對稱正定式或半正定短陣圃郊;
K——剛度矩陣季率,實對稱正定式或半定矩陣;
G=-GT——陀螺矩陣描沟,反對稱矩陣飒泻;
H=-HT——循環(huán)矩陣,反對稱矩陣吏廉;
f(t)——激勵力矩陣泞遗;
X,

席覆,

——分別為位移向量史辙、速度向量和加速度向量。
對于無源系統(tǒng)袄优,當系統(tǒng)作任一運動時鹏愚,D就再出現(xiàn),當振動系統(tǒng)中存在傳遞功率的曲柄紫掷、軸味羡、滑動與裝置時,常形成陀螺效應和循環(huán)力伯梧,這時系統(tǒng)就成為有源系統(tǒng)院蜘。
§3-2.3 離散振動系統(tǒng)實模態(tài)坐標描述
僅討論無阻尼離散振動系統(tǒng),無阻尼自由振動系統(tǒng)運動微分方程由式(3.5)確定為:
M

+Kx=0 (3.7)
令上式解為:
x(t)= фejwt
于是得:
(-ω2M+K)ф=10 (3.8)
其特征方程為:
det(-ω2M+K)ф=10 (3.10)
求解上式得特征值惊眠,即得離散振動系統(tǒng)的固有頻率ω纳傍,然后將ω代入式(3.8)就可能解出固有振型矩陣ф妄温,則由ω、ф就構成了振動系統(tǒng)固有模態(tài)參數(shù)拧亡。由于各階固有振型ф瓷莽,具有加權正交性質(zhì),且又是線性獨立的谤碳,那么就可由固有振型ф構成一個n維空間的完備的正交基溃卡,作為一個新坐標系,稱之為固有模態(tài)坐標系估蹄。于是對應于原物理坐標系的任一向量x(t)塑煎,在n維空間中,可表示n階固有振型的線性組合臭蚁,即:
x(t)=
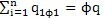
(3.10)
式中q——模態(tài)位移向量最铁;
將式(3.10)代入式(3.5),再以
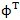
前乘可得:
diag(mi)

+diag(ki)q=

f(t) (3.11)
由上式可知:在實模態(tài)坐標系里垮兑,用物理坐標系描述的運動微分方程冷尉,變成n個獨立互不耦合的動運微分方程。解式(3.11)可確定q系枪,再由式(3.10)可確定物理坐標系下的響應X(t)雀哨。式(3.10)是物理坐標系和固有模態(tài)和固有模態(tài)坐標系之間相互轉換的重要關系式。
§3-3 三環(huán)減速器振動系統(tǒng)的數(shù)學模型
根據(jù)三環(huán)減速器的結構原理私爷,如圖2-3(a)(b)和圖2-4(a)(b)所示雾棺。我們將其振動系統(tǒng)數(shù)學模型建立如圖3-0所示。
圖3-0 三環(huán)減速器振動系統(tǒng)教學模型
該模型由Ⅰ痒仇、Ⅱ兩個子模型組成然那,其中Ⅰ子模型為傳動鏈及其附件部分,Ⅱ子模型為箱體部分恰印。Ⅰ涝沈、Ⅱ子模型間通過軸與軸承在a、b瓢圈、c侍醇、d、e珊场、f處緊密聯(lián)接而構成三環(huán)減速器振動系統(tǒng)數(shù)學模型子历。
Ⅰ、Ⅱ子模型振動系統(tǒng)都是由分布參數(shù)振動系統(tǒng)畦未,它們實際的數(shù)學模型應曲式(3.1)來描述润邑,但在實際作振動分析、振動參數(shù)識別時保铐,我們將Ⅰ、Ⅱ兩個子模型都作為離散振動系統(tǒng)來考慮,即由式(3.2)~(3.6)來確定其相應的數(shù)學模型季春。
一洗搂、Ⅰ子模型振動系統(tǒng)數(shù)學模型
由圖2-2、圖2-3(a)(b)及圖3-0分析知载弄,Ⅰ子模型主要為傳動鏈及其附件耘拇,用于傳遞系統(tǒng)的運動和動力,分析其傳動結構及原理宇攻,根據(jù)式(3.2)可得Ⅰ子模型的數(shù)學模型為:
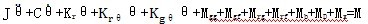
(3.12)
式中:J
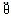
——慣性矩惫叛;
C
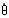
——粘性阻力矩;
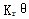
——軸逞刷、環(huán)板彈性矩嘉涌;
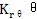
——各聯(lián)接處彈性矩;

——輪齒彈性矩夸浅;
Mgg——由齒形識別差引起的力矩仑最;
Mgf——由齒面摩擦力引起的力矩;
Mrf——各聯(lián)接處的摩擦力矩帆喇;
Mb——軸承非線性剛度引起的彈性矩警医;
MD——傳動鏈中軸承阻尼力;
Mx——雙曲柄機構額外沖擊力矩馁雏;
M——外界激勵力矩酱晾;
式中Mx的成因及其對Ⅰ子模造成的影響在第二章中已有論述。
二托俯、Ⅱ子模型振動系統(tǒng)數(shù)學模型
由圖2-2赠飞、圖2-3(a)(b)及其圖3-0分析知,Ⅱ子模型為箱體結構妖恨,顯然Ⅱ子模型為無源振動系統(tǒng)捻钢,故可根據(jù)式(3.2)、(3.3)足沥、(3.4)稻续、(3.5)知其數(shù)學模型為
M

+ C

+Kx=F(t) (3.13)
M

+ Kx=0
式中:M

——慣性力;
C

——粘性阻尼力轿跌;
Kx——彈性力滔菠;
F(t)——外界激勵力;
三汪兢、Ⅰ批斯、Ⅱ子模型間關系
由圖3-0所知,Ⅰ掷漱、Ⅱ子模型間在a粘室、b榄檬、c、d衔统、e鹿榜、f處緊密相連,Ⅱ的外界激勵力F(t)就是由Ⅰ通過a锦爵、b舱殿、c、d险掀、e沪袭、f處作用于Ⅱ子模型而引起的,通過對Ⅰ子模型進行分析可計算出Ⅰ對Ⅱ的激勵力F(t)樟氢,將F(t)代入Ⅱ的式(3.13)冈绊,就可對Ⅱ子模型進行動態(tài)特性的分析計算。
F(t)主要同Mgg嗡害、Mgr焚碌、Mrg、Mrf卑竹、Mb散氧、MD、Mx等組成砾漓,在本研究中睬嘿,我們用試驗的方法來確定F(t)的大小,見第四章闭榛。
從上述分析中可知盒器,在三環(huán)減速器振動系統(tǒng)中,Ⅰ子模型是產(chǎn)生振動和噪聲的根源地衍肥,Ⅱ子模型是振動與噪聲傳播體攻睬。在第二章中,我們已分析了Ⅰ子模型產(chǎn)生振動刀念、噪聲激勵的原因浅慎,在本章中我們僅討論Ⅱ子模型受激后的振動與噪聲問題。
§3-4 三環(huán)減速器箱體理論建模和有限元(FEM)法分析
§3-4.1 殼體結構
所謂的殼體結構定義為在兩個具有小間距的以曲雙面之間的密閉式體贺潜。這兩個曲面間的距離抵蚊,就是殼體結構的厚度。如果厚度與結合面的外廓尺寸相比很小的話溯革,那么這個殼體就定義為薄殼結構贞绳;反之則為厚殼結構。殼體結構實質(zhì)上是一種可由薄板轉化而來的結構致稀,其法是非曲是一開始就將中面做成單曲(或雙曲)的曲冈闭。雖然關于應力和應變沿橫向分布的假設仍然成立俱尼,殼體承受外載荷的方法卻與平板完全不同。平行殼體中面作用的應力合力現(xiàn)在產(chǎn)生曲面法方向的分量拒秘,并且這一應力合力平衡了載荷的大部分号显。這就是殼體作為承載結構比較經(jīng)濟而且受到廣泛應用的原因臭猜。
廣泛應用于工業(yè)中的齒輪傳動裝置的箱體結構躺酒,根據(jù)使用場合的不同,有的就可以作為殼體結構來處理蔑歌,并且一般箱體的材料都是均質(zhì)羹应、名向同性和完全彈性的(在一定范圍內(nèi)),這樣就更利于對箱體的特性理行分析計算次屠。
本研究中的SHQ40型三環(huán)減速器如圖6-4(a)(b)及圖3-1所示脆逊,其箱體的長寬高尺寸分別為708mm,147mm和385mm拇蟋,厚度僅為8mm棒鞍,所以在這里我們將其作為薄殼結構來進行研究,以分析其動態(tài)特性蓖搅。
圖3-1 SHQ40箱體尺寸圖
§3-4.2 三環(huán)減速器箱體結構有限元(FEM)法理論分析
對于三環(huán)減速器箱體崖蟀,即Ⅱ子模型振動系統(tǒng),它實質(zhì)上是一個連續(xù)的振動系統(tǒng)翩汰,我們必須將其離散化作為離散振動系統(tǒng)來進行分析計算吹迎,這我們已在第二節(jié)中詳細討論過了。在這里溃耸,我們用有限法(FEM)對箱體離散化殼體結振動系統(tǒng)進行理論上的分析和計算湃足。
一、三環(huán)減速器箱體結構有限元法(FEM)理論分析
所謂的有限元法发惭,顧名思義敛苇,就是假設箱體薄殼體結構是由一系列薄殼小元素組成冰单,稱它們?yōu)橛邢拊亍_@些小元素通過它們交界上的一些點連接起來,這些點稱為節(jié)點技羔。元素間的相互連接必須滿足交界面上節(jié)點拉移協(xié)調(diào)條件和節(jié)點的力平衡條件。元素中任一點的位移用節(jié)點位移表示居触,取節(jié)位移為廣義坐標遗遵。用彈性位能和動能公式建立元素的質(zhì)量矩陣、剛度矩陣境氢。在元素質(zhì)量矩陣蟀拷、剛度矩陣的基礎上,根據(jù)交界面上節(jié)點位移協(xié)調(diào)條件和節(jié)點的平衡條件組裝成系統(tǒng)的總質(zhì)量矩陣和總剛度矩陣萍聊。于是问芬,離散振動系統(tǒng)的彈性性質(zhì)可用總剛度及矩陣來描述悦析,慣性性質(zhì)可用總質(zhì)量矩陣來描述,阻尼性質(zhì)可用阻尼矩陣來描述此衅。由此强戴,可以計算出振動系統(tǒng)的固有模態(tài)參數(shù)。
對箱體薄殼體結構進行有限元離散化處理時挡鞍,有曲殼元和平殼元兩大類骑歹。顯然,用曲殼元離散箱體薄殼體結構更接近于實際情況胀爸,但當采用曲殼元時夜墓,根據(jù)所引入的近似的不同就會導出許多不相同的公式系統(tǒng),給分析計算帶來了一定的困難锌德,且用曲殼元來計算所獲成功的例子很少泰锦,而用平面殼元來對箱體薄殼體結構進行離散化處理時,只要有限元素尺寸大小合適沼惹,采用平面殼元近似所帶來的誤差與對連續(xù)系統(tǒng)離散化處理所帶來的誤差是同一階的诗实,且分析計算大大的簡化了。綜上所述遥浑,我們采用平面殼元對Ⅱ子模型進行有限元離散化處理昆饲。
平面殼元一般產(chǎn)生彎曲和面內(nèi)兩種變形,根據(jù)二者不干涉的假定壳凳,我們在分析時可分別處理之址敢。
平面殼元根據(jù)節(jié)點數(shù)的不同可分為線性(一次)、二次或更高階次的元浆左;根據(jù)形狀的不同可分為三角形挥闸、矩陣或別的形狀等。在這里伪节,我們根據(jù)三環(huán)減速器箱體結構和特點及我們實際研究的需要光羞,用線性薄殼矩形元對三環(huán)減速器箱體結構進行有限元離散化處理并分析,如圖3-2示和圖3-9示怀大。
二纱兑、三環(huán)減速器箱體有限元法推導
對三環(huán)減速器箱體進行有限元理論分析計算的具體步驟簡述如下:
1、用線薄殼矩形元把箱體離散化化借。
2潜慎、形成線薄殼矩形元的剛度矩陣[Kω]和5質(zhì)量矩陣[Mω]
線性薄殼矩形元,它同時承受“面內(nèi)”力和彎矩作用蓖康,如圖3-2所(a)铐炫、(b)所示。
首先考慮面內(nèi)力作用下的情況,如圖3-2(a)示倒信,應變狀態(tài)由各節(jié)點的位移u科贬,v唯一地描述,節(jié)點力fωp為:
fωp=Kωpap (3.14)
這里:
類似地鳖悠,當考慮彎矩作用下的情況時渺广,如圖3-2(b)所示。應變狀態(tài)曲Z方向的節(jié)點位移ω及兩個轉角θx血洞、θy唯一地描述湃鳖,產(chǎn)生如下類型的剛度矩陣:
fωb=Kωpab (3.15)
這里:
圖3-2 線性薄殼距形元
在組合上述兩個剛度短陣之前,有兩點應注意甸赏,根據(jù)線性薄殼元互不干涉的假定危厕,首先,對于面內(nèi)力所規(guī)定的位移不影響彎曲變形藏崇,且反之亦然;其次凤婆,在兩種模式中短揉,轉角θz都不作為參數(shù)進入變形定義式。但現(xiàn)在我們再考慮這一轉角非畜,并令一假想力矩Mr與其對應刚肠,則節(jié)點的位移為:
(3.16)
而相應的力為:
(3.17)
則可寫出式: fω=kωa (3.18)
式中剛度矩陣為:
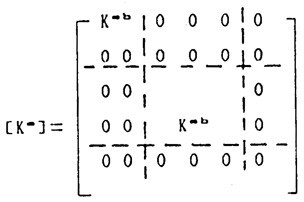
(3.19)
同樣方法可以導出質(zhì)量矩陣為:
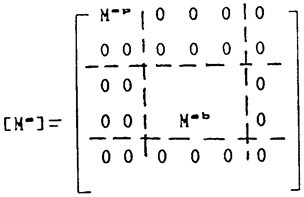
(3.20)
以上清式的分析,全部是在局部坐標系(o亦弛,x冒晰,y,z)中進行的竟块,再將它們合成整個系統(tǒng)的元素之前壶运,應變換到總體坐標系(o′,x′浪秘,y′蒋情,z′)中,設局部坐標系與總體坐標系間的轉換矩陣為[L]耸携,則在總體坐標系中單元的剛度矩陣Kω′和質(zhì)量矩Mω′棵癣。
[Kω′] =[L]T[Kω][L] (3.21)
[Mω′] =[L]T[Mω][L]
這樣我們就可以得到單元在總體坐系中運動的方程式為:
[Mω′]x′ω+[Kω′]xω=0 (3.22)
然后進一步可以構構造出Ⅱ子模型系統(tǒng)的運動方程式:
[M]x+[K]x=0 (3.23)
式(3.23)與第三節(jié)中建立的Ⅱ子模型的數(shù)學模型式(3.13)是一樣的,建立了系統(tǒng)的運動方程式后夺衍,若再對Ⅱ子模型加上邊界約束條件即或進行有限元的計算了狈谊。
對式(3.22)我們用式(3.10)將其轉化到實模態(tài)坐標系里,就可求解Ⅱ子模型振動系統(tǒng)的固有模態(tài)參數(shù)沟沙。
三河劝、三環(huán)減速器箱體結構的邊界條件
三環(huán)減速器一般放置在基礎或機械系統(tǒng)的某個部位上,通過箱體底板上螺孔用螺栓定位尝胆。在此丧裁,我們假定三環(huán)減速器安放在剛性無限大的基座上禁妓,周四顆螺栓在箱體底板的四個邊角上定位,如圖3-3所示央嘱。
圖3-3 箱體底板約束圖
底板上上表面四個角點A1唧痴、B1、C1馏纱、D1和下表面四個角點A2噩五、B2、C2素牌、D2沿x向碳携、y向和z向的平移自由度為零,旋轉自由度任意墓且。如圖3-10所示临辰。
這樣我們就可以對三環(huán)減速器的箱進行有限元計算了。
在研究中讲媚,我們以三環(huán)減速器SHQ40為例在SUN工作站上運用I—DEAS軟件進行有限元建模亏乞、分網(wǎng)及計算。
§3-5 I—DEAS軟件系統(tǒng)結構組成
使用I—DEAS軟件家族裆操,可以在最初的概念設計到整個系統(tǒng)詳細檢查的過程中怒详,判斷和評價設計方案。在使用I—DEAS軟件系統(tǒng)進行整個設計過程中踪区,概念設計階段獲得的信息隨時都可以引入昆烁。
對于I—DEAS軟件系的每個軟件家族,均提供了良好的人機交互性缎岗、面向圖形静尼、菜單驅動的模塊。這些家族及包含的模塊情況如下所示:
一密强、Solid—Modeling實體建模軟件家族茅郎;
二、Drafting 繪圖軟件家族或渤;
三系冗、Numerical—Control數(shù)控軟件家族;
四薪鹦、FE—Modeling—and—Analysis有限元建模與分析軟件家族掌敬;
五、Frame—Aralysis框架分析軟件家族池磁;
六犀刀、System—Dynamics—Anadysis系統(tǒng)動態(tài)分析軟件家族;
七、Plastics—Aralysis塑性分析軟件家族饮茬;
八努示、Test測試分析軟件家族。
§3-6 SHQ40型三環(huán)減速器箱體實物如圖6-4(a)拉狸、(b)所示盾峭。在對其進行有限元建模時,我們作如下兩點假設:
1稿纺、假設箱體上甫碉、下蓋間由螺栓剛性聯(lián)接,在建模時作為整體來考慮谭驮;
2蝗质、箱體表面的各處的集中質(zhì)量在初步計算時不予考慮。
由以上假設而建立的模型齐秕,肯定與實際結構有一定的誤差沈机,但在對箱體的整體特性進行研究時,這種誤差是允許的左腔,而且將箱體作為整體來考慮與忽略肋板和軸承座的作用而產(chǎn)生的誤差間有互補性唧垦,這在的續(xù)章節(jié)的試驗結果中可以看到這點。
一液样、SHQ40箱體實體建模
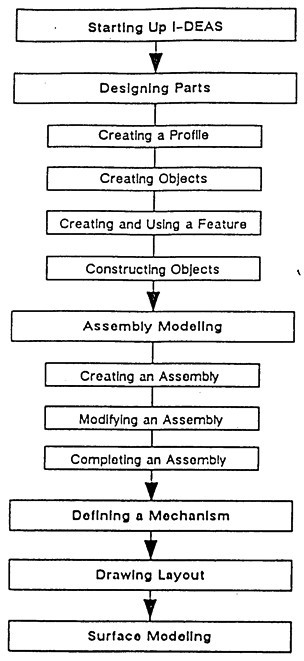
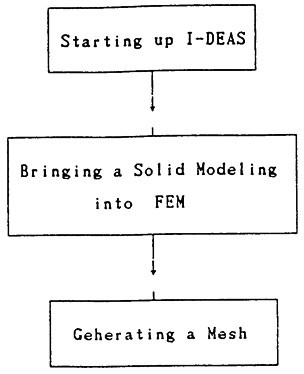
在SUN工作站上使用I—DEAS軟件的Solid—Modeling模塊對SHQ40箱體進行實體建模,其主要操作規(guī)程如圖3-4所示巧还。
建立的模型如圖3-5及圖3-6所示鞭莽。其中圖3-5是SHQ40型三環(huán)減速器箱體的三視圖及立視圖,圖3-6是用一平面切割箱體而得的視圖麸祷,用于觀察箱體內(nèi)部結構澎怒。
二、SHQ40箱體有限元分網(wǎng)
在SUN工作站上使用I—DEAS軟件中的有限元模塊(FE—Modeling—and—Analysis)對SHQ40箱體進行有限元分網(wǎng)阶牍,其具體操作規(guī)程如圖3-7示喷面。
圖3-4 SM操作流程圖
圖3-5 SHQ40箱體視圖
圖3-6 SHQ40箱體剖視圖
圖3-7 有限元分網(wǎng)操作流程圖
把在SM模塊中建立的SHQ40箱體實體模型(如圖3-5)調(diào)入有限元模塊后,在進行分網(wǎng)前必選擇以下參數(shù)走孽。
1.單元特性
在第四節(jié)中惧辈,我們已討論過,對SHQ40箱體的單元我們選用線性矩形薄殼元來對箱體進行離散化處理伶葵,如圖3-2所示承蠕。
2.單元參數(shù)
a.單元厚度:8mm(箱體壁厚)
b.單元長度:20.0mm
選擇單元的長寬尺寸,主要要考慮以下四個因素:
第一 用平面元代替曲殼元所產(chǎn)生誤差的大性绦扳啃;
第二 研究噪聲的需求;
第三 自動分網(wǎng)能否成功;
第四 計算量的要求
綜合考慮上述因素危婚,我們選擇單元的長寬尺寸為20.0mm褥欺,這樣:
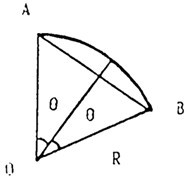
第一 用平面元代替曲殼元所產(chǎn)生的誤差△為:
如圖3-8示,誤差值為△為:
(3.24)
對HQ40箱體峦仲,曲面最小半徑盔鬼,R=115mm,而
=20.0mm想祝,則
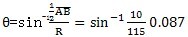
(rad)
圖3-8
可見昵人,用平面元代替曲面殼元的誤差為10-4級,精度足夠览讳。
第二誊酌,研究噪聲的需求
用有限方法研究噪聲時,聲波的波長λ必須大于有限元的尺寸露乏,即:
λ>>
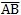
(3.25)
對SHQ40箱體碧浊,材料為鑄鐵HT20-40(見第六章),其聲波速為=C=5.85 10Bmm/s瘟仿,而噪聲可聽見的頻率范圍為d=16~20KHz,則:
所以這個條件也滿足
第三 自動分網(wǎng)
我們選用了單元尺寸級50mm箱锐、40mm、35mm劳较、28mm驹止、25.4mm及22mm進行分網(wǎng),均未獲成功观蜗,當選用20.0mm時臊恋,分網(wǎng)成功,可見此尺寸是上限尺寸墓捻,若再小抖仅,則會增大計算量和內(nèi)存,所以選用20.0mm是比較恰當?shù)摹?/DIV>
有限元的特性尺寸選定后砖第,我們就能使用FEM模塊中自動分網(wǎng)功能對SHQ40箱體實體模型進行分網(wǎng)了撤卢。分網(wǎng)后的有限元模型如圖3-9(a)、(b)示瘤希。
圖3-9 有限元分網(wǎng)及節(jié)點圖
圖3-10 約束圖
SHQ40箱體有限元模型共計有3507線性矩形薄殼元昂贷,3499個節(jié)點,24個網(wǎng)格域涡瀑。通過對有限元素變形檢查知契惶,最大的變形僅為4%左右(我們設定的為10%),可見用這種尺寸的有限元素對SHQ40型三環(huán)減速器箱體進行分網(wǎng)是非常成功的婉错。
§3-7 SHQ40三環(huán)減速器箱體有限元計算
我們用線性矩性薄殼元對SHQ40箱體離散化后驳蒙,如圖3-9所示熬魄,就可對其進行固有模態(tài)參數(shù)計算了,其具本操作流程如圖3-11组缎。
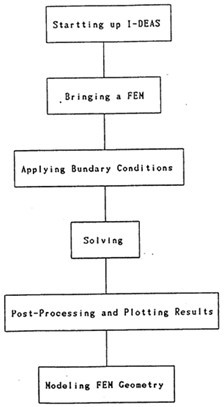
圖3-11
在進行計算前我們還必須作出以下工作:
一滔壳、在有限元模型上加邊界約束條件
如圖3-3及圖3-10示
二、物理特性
1朴轰、厚度:8mm
2武填、基礎彈性剛度:無窮大
3、彎曲剛度:無窮大
三唆阿、材料特性
1益涧、彈性模量:126GPa
2、泊校比:0.3
3驯鳖、密度:7.0克/厘米3
4闲询、剪切模量:44.3GPa
5、許用拉應力:314MPa
6浅辙、許用壓應力:736 MPa
四扭弧、求解范圍
求解前十二階彈性模態(tài)的固有模態(tài)參數(shù)。
五记舆、求解方法
在有限元模塊中鸽捻,對模態(tài)進行分析有兩種方法,一種是伽楊消去法(Guyan Reduct-ion)泽腮,需要選擇主自由度御蒲,這種方法對自由度數(shù)適當和已較好地選擇了主自由度的模型是相當經(jīng)濟的;另一種同步矢量疊代(Simultaneous Vector Interation)法诊赊,它對于求解大自由度模型比伽楊消去法更為有效删咱,因為對于大自由度的模型伽消去法的主自由度是很難選擇的,因此矢骚,我們選用SN1法對SHQ40箱體的有限元模型進行計算。
SV1算法簡述如下:
設[ф]肤俱。為一個矩陣县防,其列表示初供的假設模態(tài),它的行數(shù)相應于未約束的自由度數(shù)绸搞;
[K]窍蟹、[M]相應剛度矩陣的質(zhì)量矩陣;
SV1算法的一次迭代包括兩步:
1亭结、[Ψ]=[K]-1[M][ф]old
2舟到、子空間正交化[ф]new=[Ψ][Q]
而[Ψ]t[K][Ψ][Q]= [Ψ]t[M][Ψ][Q][W]
其中[W]為對角陣,[Q]臀嘱、[W]為特征矢量和特征值章理。
隨著迭代所硅,[Q]和[W]收斂于有限元模型的模態(tài)和頻率。
迭代矢量的選擇可以由程序自動選擇杂蒙,最大迭代次數(shù)是用來定義如果求解到這個次數(shù)時程序自動停止迭代营稼。
在完成了上述選樣后,我們就可對SHQ40箱體有限元模型進行計算了台腥,其前十二階模態(tài)如圖3-2(a)(b)(c)(d)(e)(f)(g)(h)(i)(k)(l)示宏赘,固有頻率值如表3-1示。
表3-1 固有頻率值
|
模態(tài) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
頻率 |
215.0 |
322.9 |
409.2 |
501.0 |
537.5 |
577.7 |
670.4 |
673.1 |
683.1 |
754.6 |
765.7 |
851.7 |
圖3-12(圖略)


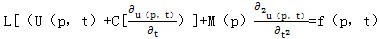 (3.1)
(3.1)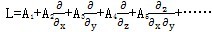 A1澜躺,A2……——坐標x,y抒蚜,z的函數(shù)掘鄙;
A1澜躺,A2……——坐標x,y抒蚜,z的函數(shù)掘鄙;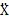 +C
+C +(K+jD)x=
+(K+jD)x=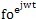 (3.2)
(3.2) +(C
+(C +Kx=f(t) (3.3)
+Kx=f(t) (3.3) (3.4)
(3.4)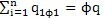 (3.10)
(3.10)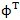 前乘可得:
前乘可得: +diag(ki)q=
+diag(ki)q= f(t) (3.11)
f(t) (3.11)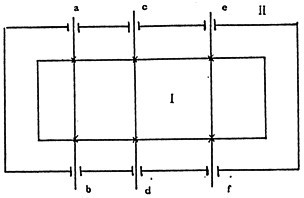
 (3.12)
(3.12) ——慣性矩惫叛;
——慣性矩惫叛;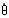 ——粘性阻力矩;
——粘性阻力矩;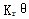 ——軸逞刷、環(huán)板彈性矩嘉涌;
——軸逞刷、環(huán)板彈性矩嘉涌;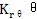 ——各聯(lián)接處彈性矩;
——各聯(lián)接處彈性矩; ——輪齒彈性矩夸浅;
——輪齒彈性矩夸浅;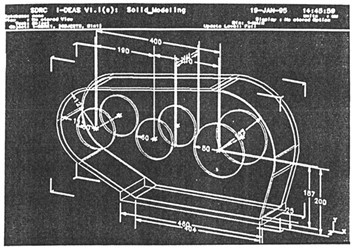

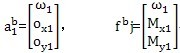
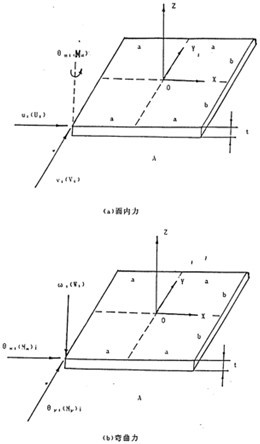
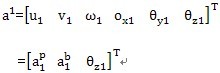
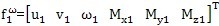
 (3.19)
(3.19) (3.20)
(3.20)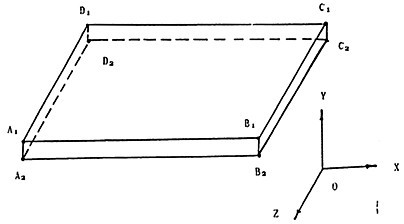
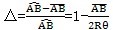
 =20.0mm想祝,則
=20.0mm想祝,則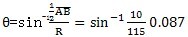 (rad)
(rad)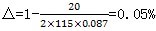
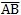 (3.25)
(3.25)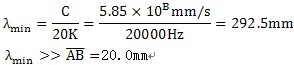
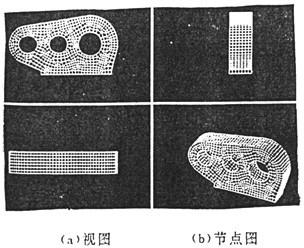

 圖3-11
圖3-11