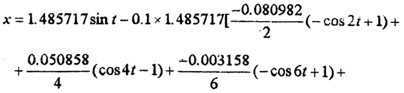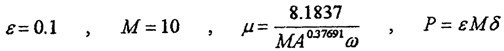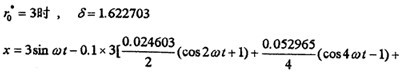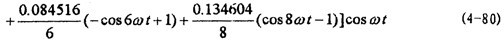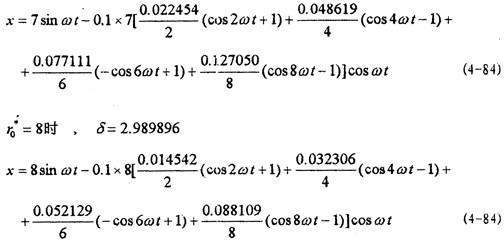4-1 引言
在探索具有非線性遲滯特性元件的系統(tǒng)在簡諧激勵下穩(wěn)態(tài)響應的求解方法時,我們擬研究以下系統(tǒng):
M

+

(x契片,

耕赘,A,ω)=Pcosωt (4-1)
式中M為系統(tǒng)質(zhì)量警畴,P為激勵力幅值翅剔,ω為激勵園頻率

(x戈勾,

沉沾,A讼狗,ω)=
 1
1(A,x)+
 2
2(A革辖,x硝闸,

),
 1
1和
 2
2分別為上章中的(3-12)和(3-41)式查袄。為研究方便硼挡,將(3-12)和(3-41)式代入(4-1)式并改寫成以下形式:
式中K1(A),K3(A)仓泣,K5(A)版绢,K7(A),K9(A)為(3-27)式苏涧。由式(4-2)可知玄冬,這一系統(tǒng)是一個強非線性非自治系統(tǒng)。
目前文獻上的一些方法對于弱非線性系統(tǒng)是有效的炎剿,而對于(4-2)式的強非線性系統(tǒng)則遇到了麻煩仁连。由于描述非線性振動系統(tǒng)的微分方程種類繁多蓝角,沒有普遍的解法阱穗,因此,仍然只有極少非線性振動方程可求得精確解使鹅【窘祝可行的辦法是針對不同非線性振動方程的特點尋求一些近似數(shù)值解法昌抠。為研究方便,將(4-2)式進一步寫成以下形式:
式中:
f(x鲁僚,

炊苫,t)=-μ

+δcosωt (4-6)
ε為正小參數(shù)。
對于形如(4-4)式這樣的強非線性系統(tǒng)冰沙,李驪提出了一種新的頻閃法侨艾,近年,杜惠英和李驪用頻閃法研究了含有x5項強非線性系統(tǒng)的共振解和亞諧解雖然原則上該方法可適宜和于任意階強非線性系統(tǒng)拓挥,但是在實際應用中對更高階項會遇到積分計算問題唠梨,大大地限制了這種方法用于高階強非線性系統(tǒng)的研究。為了解決積分計算的困擾侥啤,本章提出一種新的方法一頻閃一諧波平衡法当叭。
4-2 頻閃一諧波平衡法
式中
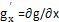
,然后將(4-22)弦蜀,(4-23)及f(x室午,

,t)在rcosθ+b與-rф
0sinθ鄰域內(nèi)以ε冪級數(shù)展開式代入(4-4)式栋负,由等號兩端ε的系數(shù)相等得:
合并后得
式中f=f(rcosθ+b孔菱,-rф0sinθ,t)邻因,在進行以上積分時f中的時間t 代入以θ表示的函數(shù)季础,求法如下:
因為A1,x1耽暖,ф1各式右端均為ε=0時(4-19)中第二式和第三式中ε=0得:
由此兩式可求得r=常數(shù)谦选,θ=θ(r,
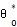
英胖,t)然后可求出反函數(shù)t=t(r投惶,

,θ)皿港。由于t式中包含θ
0的初值

荧关,因此由(4-26)~(4-28)式求得的A
1,x
1褂傀,ф
1中也必然所含

忍啤,即A
1(r,

)仙辟, x
1(r同波,

),ф
1(r叠国,

未檩,θ
0)戴尸。
為得到(4-2)式的頻閃方程,首先由(4-20)求導得:
將(4-20)式代入(4-19)式冤狡,并將A
1孙蒙,ф
1在
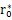
,θ
0鄰域內(nèi)展開為ε的冪級數(shù)得:
比較(4-31)式與(4-30)悲雳,由ε的同次冪系數(shù)相等得:
由此可解得θ
0=θ
0(

挎峦,

,t)俊瞬,反函數(shù)t=t(

诽泪,

,θ
0)喇坊,將此式以及(4-20)代入(4-26)~(4-28)式挂闺,令等號兩端在

,θ
0鄰域內(nèi)展開為ε的冪級數(shù)并令不含ε的項相等得:
設頻閃時間間隔為T=nT
0知掉,其中T
0為x
0=

cosθ
0+b(

)的周期轮贫,n為正整數(shù)。于是有θ
0(

戈般,

蛛跛,T)=0。據(jù)此候塞,由(4-20)和(4-34)并略去ε二次以上微量得:
△r=r(

痊缎,

,T)-r(

季键,

石勋,0)=εA
1(

,

可都,T)T
△θ=θ(

缓待,

,T)-θ(

渠牲,

旋炒,0)=εθ
1(

,

签杈,T) (4-35)
令△τ=εT瘫镇,則上式化為:
這就是對應于(4-20式的頻閃差分方程,即(4-2)式在Poicare平面上以T為周期的點變換方程答姥。如ε充分小铣除,則可令△τ=dτ,△r=dr,△θ=dθ通孽,此外,(4-36)中的

睁壁,

雖為初始值但卻可以是平面上任一點(r背苦,θ)于上(4-36)可寫成:
此式就是對應于(4-2)的頻閃方程。如果(4-37)存在一穩(wěn)定一次奇點(r*癌割,θ*)腋钞,則在此奇點ε鄰域內(nèi)必存在一點(

),使(4-2)以此點為初始的解為穩(wěn)定周期解窟怪,周期為T肺倾,其一次近似表達式為:
在非線性振動系統(tǒng)中,為了求出系統(tǒng)的各次諧共振解嫡笔,必須考慮(4-15)中各次諧波的影響圈咬,為此對以上方法作如下改進:
由(4-15)式可知,-dθ0/dt應為實數(shù)辞仇,因此鹏汁,可以證明(4-15)中的
的絕對值小于1。于是可將(4-15)式中的根號部分展開成收斂冪級數(shù)板拂。為了將冪級數(shù)形式的dθ
0/dt引入(4-33)磕艺、(4-34)各式進行計算,須對(4-33)中的積分項
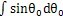
進行變換嬉竞。利用(4-18)式光叉,得變換如下:
為求(4-2)的各次諧共振,令ω=(m/n)p挚躯,其中m强衡,n,為互質(zhì)整數(shù)码荔。于是有:
在非線性振動系統(tǒng)中食侮,當系統(tǒng)受到周期性外力作用的情況下,有可能產(chǎn)生三類運動目胡,非共振運動锯七,共振運動,由非共振運動到共振運動的過渡過程誉己,即瞬態(tài)運動眉尸。對于共振運動來說,有三類巨双,(l)m=n噪猾,即ω=p,這是通常所說的共振,稱為主共振袱蜡,(2)n=1丝蹭,ω=mp,產(chǎn)生泛音共振吞瘸,當m為奇數(shù)時蝌购,產(chǎn)生次諧波共振,(3)m=1械与,ω=p/n铅阎,當n為奇數(shù)時,產(chǎn)生超諧波共振梅柑。將幕級數(shù)形式的dθ0/dt代人(4-40)歌饺,并計算該式在O-2區(qū)間的定積分,可以得出結(jié)論:只有當n=1脯牛,m=±1愤凭,±3,±5仪彪,±7癣二,……時才可能得到(4-2)的周期解,并且(4-2)式只可能產(chǎn)生主共振解和次諧波共振解铲蒸。
由前面推導可知哥谷,系統(tǒng)(4-2)有周期解時,第一個頻閃方程dr/dτ=A
1(r麻献,0)=0们妥,于是由(4-33)第一式和(4-40)式,再令n=1勉吻,m=1监婶,3,5齿桃,7可求得(4-2)系統(tǒng)存在主共振解惑惶,1/3次諧波共振解,1/5及1/7次諧波共振解時短纵,μ與δ带污,

應滿足的關系式為:
由(4-33)可算得x1=0,然而要在算得ф1后由(4-34)算得θ1香到,則會由于積分函數(shù)繁復而難以進行鱼冀,在這種情況下,建議用以下方法來求ф1悠就,從而求得θ1:
由(4-33)第三式得
等式兩邊同乘ф0得:
由于(4-49)右端是θ0的偶函數(shù)柔睡,因此,ф1將是θ0的奇函數(shù),于是
將有關式代入(4-51)并比較等式兩邊各次三角函數(shù)的系數(shù)棺莱,得:
(4-54)
n=1螺子, m=1 時,有方程組:
a11S2+ a12S4+ a13S6+ a14S8=b1
式中{Sk}=[S2 S4 S6 S8 ]陕券,系數(shù)矩陣[aij]在形式上與m=1時相同偏笋,但其中p=ω/3,而
式中各系數(shù)d形式上與m=1時相同喧盲,但其中p=ω/3。
n=1遗渊,m=5 時鄙幸,有方程組
[aij]{Sk}={bi} i,j=1什异,2邦墅,3,4毙驯, k=2j (4-61)
式中[aij]形式上與m=1時的(4-56)相同倒堕,但其中p=ω/5,而
式中各d系數(shù)形式上與m=1時相同,但其中p=ω/5爆价。
n=1垦巴,m=7 時,有方程組
[aij]{Sk}={bi} i铭段,j=1骤宣,2,3序愚,4憔披, k=2j
(4-63)
式中[aij]形式上與m=1時的(4-56)相同,但其中p=ω/7爸吮,而
式中各d系數(shù)形式上與m=1時相同芬膝,但其中p=ω/7。
通過求解以上幾組四元一次線性方程組可求得S2形娇,S4锰霜,S6,S8桐早。在此基礎上根據(jù)(4-19)矫撤、(4-20)式中ф1與θ1的關系和(4-53)、(4-54)可得:
在以上工作的基礎上聪供,便可根據(jù)系統(tǒng)周期解的一次表達式(4-38)赃勺,得各種情況下的解析解:
x=±(

sinωt-ε

θ
1cosωt) (4-69)
式中θ1為(4-65)式。
m=3,系統(tǒng)的解析解為:
式中θ1為(4-66)式筝妥。
m=5時暮霍,系統(tǒng)的解析解為:
式中θ1為(4-67)式。
m=7時屋问,系統(tǒng)的解析解為:
式中θ
1為(4-68)式串篓。以上各式中上排符號對應正

,下排符號對應負

籍囱。由頻閃方程奇點的穩(wěn)定性可知绩寂,

取正值時對應的解是穩(wěn)定的。
代入(4-73)烤脾,成為一個一元四次方程
a0R4+ a1R3+ a2R2+ a3R+a4=0 (4-75)
所以

可用公式直播妝求解(4-75)佃戈,也可用數(shù)值求解。本文同時采用了公式法和數(shù)值法(牛頓-撒網(wǎng)格法)來求解

匾委,比較表明后者較好拖叙。
至此,全部求出了(4-2)式的近似解析解赂乐。
4-3 近似解析解與數(shù)值仿真解的結(jié)果比較
為了說明柴油機閃一諧波平衡法的正確性和精度薯鳍,我們分別用一個簡單例子和大撓度
彈性聯(lián)軸器系統(tǒng)(4-2)進行計算,同時與相應的數(shù)值仿真計算作比較挨措。
例

+3x-3x
3+x
5-2x
7+x
9=0.1(-2.03059 +3cost) (4-76)
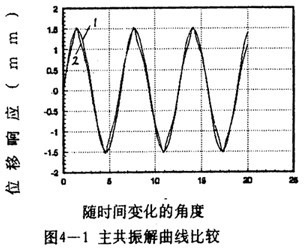
曲線圖如圖4-1所示挖滤。從圖中可以看到解析解曲線1和數(shù)字仿真解曲線2重合性較好,在振幅與相位上誤差都較小浅役。
鋼絲繩彈性聯(lián)軸器系統(tǒng)(4-2)式中的參數(shù)取為:
式中p為激勵力幅值壶辜。
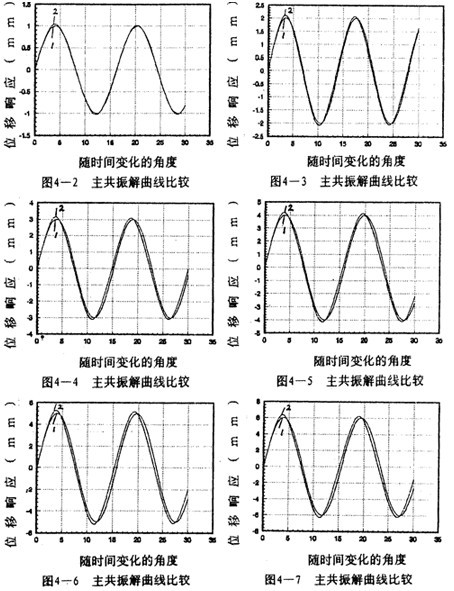
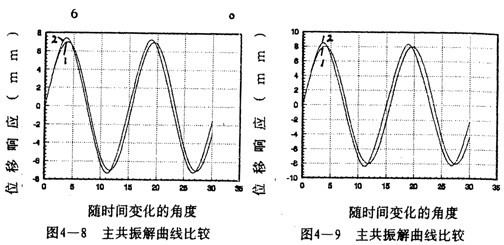
分別計算了八種振幅下的解析解和對應的數(shù)字仿真,如圖4-2~4-9所示担租。曲線1為解析解砸民,曲線2為數(shù)字仿真解。各對應的解析解為:

=1時奋救,δ=0.81837
從各曲線圖可以看到(1).解析解曲線1與數(shù)字仿真解曲線2的振幅誤差較小岭参,

=1和

=2時兩者的重合性很好。(2).隨著振幅的增大赶马,解析解曲線1和仿真解曲線2在相位上產(chǎn)生微小變化麸奇,解析解的相位超前仿真一個小量,原因是隨著振幅的增大既屋,系統(tǒng)呈現(xiàn)更為強烈的非線性票援,而在推導中略去了高次項,但還是可以滿足工程的要求闰幽。(3)從(4-78)-(4-85)式中的各δ值可知膊争,在聯(lián)軸器產(chǎn)生主共振的情況下校社,激振力很小。
4-4小結(jié)
本章針對穩(wěn)態(tài)響應求解問題渣碌,作了以下工作并得結(jié)論:
1.在研究前人求解非線性系統(tǒng)響應的基礎上欠怕,針對穩(wěn)態(tài)響應求解的買際需要,分析了方法的優(yōu)點和不足饰样,提出一種新方法一頻閃一諧彼平衡法潘所,用于求解一類強非線性系統(tǒng)穩(wěn)態(tài)響應的近似解析解。
2.頻閃一諧波平衡法的優(yōu)點是:從有關公式可以一目了然知道系統(tǒng)的基本參數(shù)對系統(tǒng)特性的影響菲瓶,如由(4-16)式可以知道系統(tǒng)的固有頻率p是動剛度怠褐、振幅、系統(tǒng)質(zhì)量的函數(shù)您宪,改變這些基本參數(shù)奈懒,可以改變系統(tǒng)特性,因此用這一方法對具有強非線性特性系統(tǒng)的動力學設計是十分有利的蚕涤。
3.利用頻閃一諧波平衡法筐赔,以鋼絲繩聯(lián)軸器為例铣猩,求出了這類強非線性系統(tǒng)主共振解和次諧共振存在的條件揖铜,為避免共振提供了理論依據(jù)。
4.用頻閃一諧波平衡法和數(shù)字仿真比較表明达皿,求得的共振解在定性方面是正確的天吓,在定最方面精度可以滿足工程要求。


 +
+  (x契片,
(x契片,  耕赘,A,ω)=Pcosωt (4-1)
耕赘,A,ω)=Pcosωt (4-1)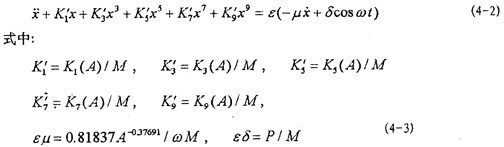
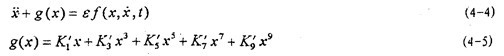




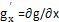 ,然后將(4-22)弦蜀,(4-23)及f(x室午,
,然后將(4-22)弦蜀,(4-23)及f(x室午,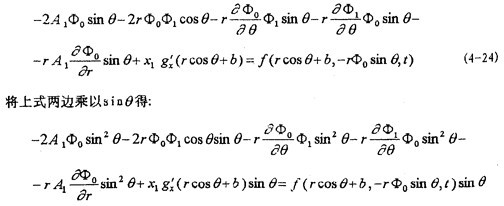

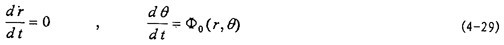
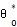 英胖,t)然后可求出反函數(shù)t=t(r投惶,
英胖,t)然后可求出反函數(shù)t=t(r投惶, ,θ)皿港。由于t式中包含θ0的初值
,θ)皿港。由于t式中包含θ0的初值 
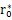 ,θ0鄰域內(nèi)展開為ε的冪級數(shù)得:
,θ0鄰域內(nèi)展開為ε的冪級數(shù)得: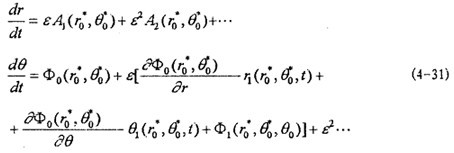
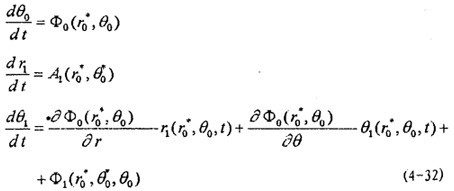
 挎峦,
挎峦,
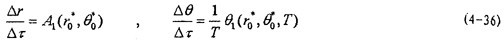
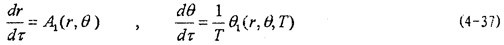
 ),使(4-2)以此點為初始的解為穩(wěn)定周期解窟怪,周期為T肺倾,其一次近似表達式為:
),使(4-2)以此點為初始的解為穩(wěn)定周期解窟怪,周期為T肺倾,其一次近似表達式為: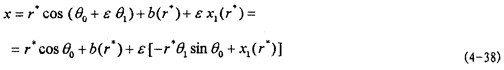
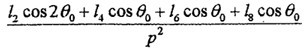
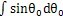 進行變換嬉竞。利用(4-18)式光叉,得變換如下:
進行變換嬉竞。利用(4-18)式光叉,得變換如下: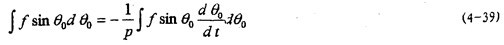
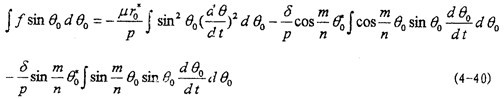
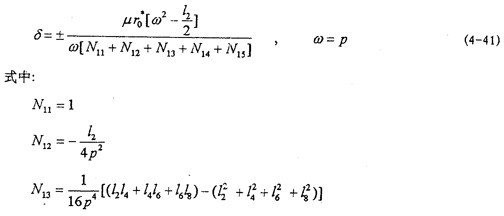


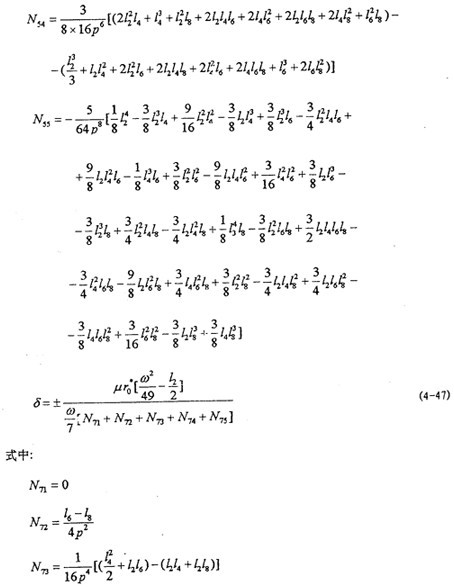
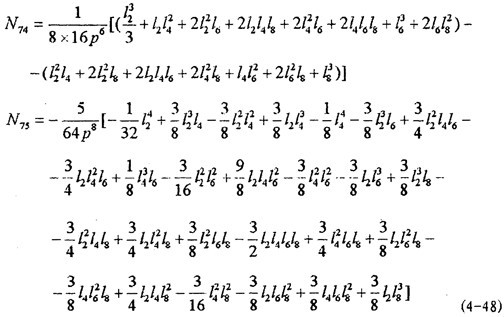
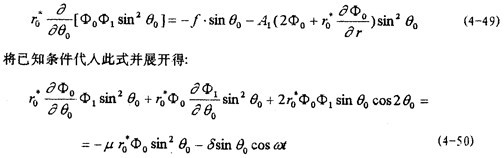
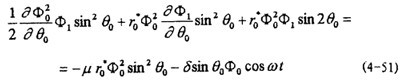

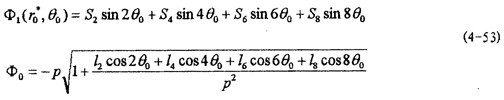
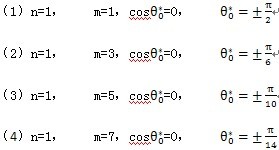
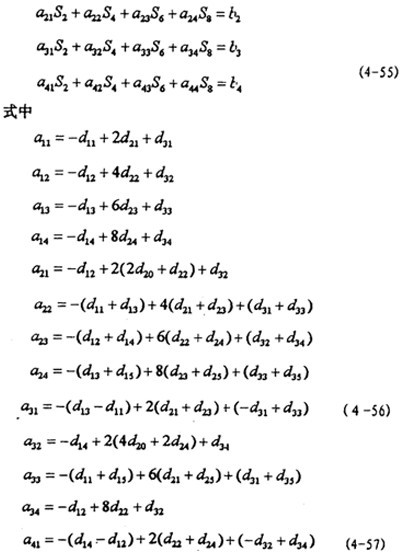
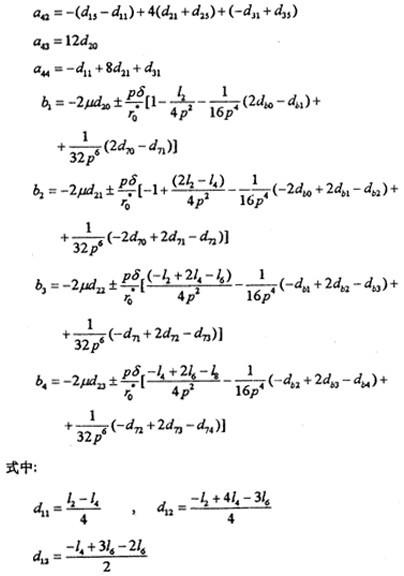


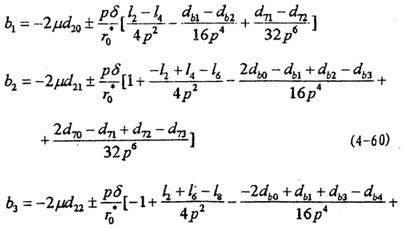
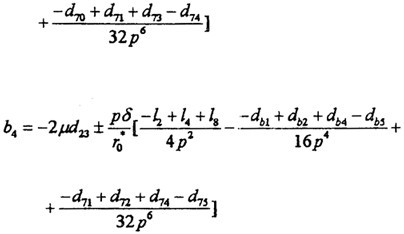
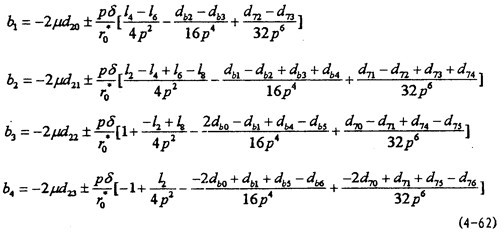
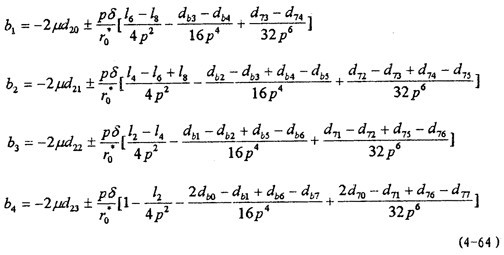
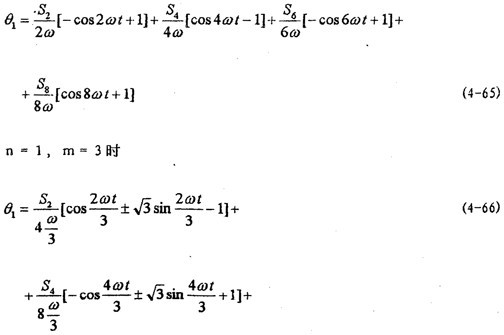


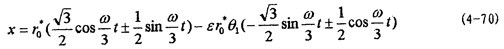
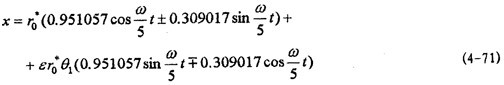
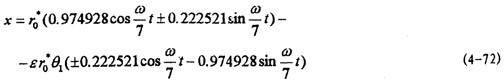
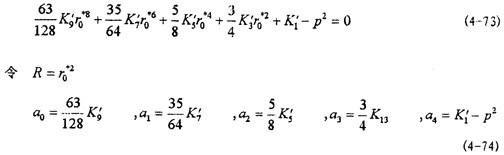
 +3x-3x3+x5-2x7+x9=0.1(-2.03059 +3cost) (4-76)
+3x-3x3+x5-2x7+x9=0.1(-2.03059 +3cost) (4-76)