具有非線性遲滯特性鋼絲繩聯(lián)軸器建模與參數(shù)辨識(shí)
3-1引言
由上章對(duì)聯(lián)軸器振動(dòng)試驗(yàn)研究結(jié)果可知斩缘,在大位移振動(dòng)情況下唁底,聯(lián)軸器表現(xiàn)出非線性遲滯特性.這一特性直接與聯(lián)軸器動(dòng)剛度及阻尼有關(guān),當(dāng)這種聯(lián)軸器用于船舶推進(jìn)軸系時(shí)泳隶,將影響到軸系的動(dòng)力特性他幢,因此弄清楚聯(lián)軸器恢復(fù)力與動(dòng)剛度和阻尼的關(guān)系涮侥,即建立聯(lián)軸器恢復(fù)力的數(shù)學(xué)模型是十分重要的,對(duì)于深人分析研究推進(jìn)軸系的動(dòng)力特性也是不可缺少的订咆。
由鋼絲繩聯(lián)軸器的  -x遲滯回線可知琅翻,聯(lián)軸器的遲滯特性不宜用雙線性模型來(lái)描述,主要原因是雙線性模型與聯(lián)軸器的動(dòng)態(tài)遲滯回線外形相差甚遠(yuǎn)柑贞,雙線性模型將系統(tǒng)剛度系數(shù)處理成二個(gè)線性剛度系數(shù)。這不足以描述鋼絲繩聯(lián)軸器的非線性遲滯特性中的非線性剛度系數(shù)聂抢,雙線性模型阻尼僅處理為干摩擦阻尼钧嘶,也不足以描述聯(lián)軸器阻尼的復(fù)雜成分。一階微分方程模型主要用于遲滯系統(tǒng)的隨機(jī)響應(yīng)分析中琳疏,這種模型用于計(jì)算遲滯系統(tǒng)的穩(wěn)態(tài)動(dòng)力響應(yīng)很不方便有决,模型中各參數(shù)的物理意義不明確,模型形式不利于各參數(shù)的辨識(shí)空盼,而且彈性力和阻尼力在恢復(fù)力表達(dá)式中不顯現(xiàn)书幕,不利于理論分析±恐海基于平均和等效原理的跡法和以此為基礎(chǔ)K0等建立的模型都有自己的不足台汇,前者只能描述遲滯恢復(fù)力與位移和速度的關(guān)系,而不能全面描述遲滯恢復(fù)力與各振動(dòng)參數(shù)的關(guān)系篱瞎,后者只能描述三個(gè)階次非線性彈簧剛度苟呐,其應(yīng)用范圍受到限制。由此可知遥局,現(xiàn)有描述遲滯特性的數(shù)學(xué)模型都不能用來(lái)描述聯(lián)軸器的非線性遲滯特性付箩。因此,本章將在前人研究的基礎(chǔ)上莽烫,研究聯(lián)軸器動(dòng)剛度和阻尼的特性瞭谴,建立既能合理描述聯(lián)軸器非線性遲滯特性又能滿足較高精度要求的數(shù)學(xué)模型。
-x遲滯回線可知琅翻,聯(lián)軸器的遲滯特性不宜用雙線性模型來(lái)描述,主要原因是雙線性模型與聯(lián)軸器的動(dòng)態(tài)遲滯回線外形相差甚遠(yuǎn)柑贞,雙線性模型將系統(tǒng)剛度系數(shù)處理成二個(gè)線性剛度系數(shù)。這不足以描述鋼絲繩聯(lián)軸器的非線性遲滯特性中的非線性剛度系數(shù)聂抢,雙線性模型阻尼僅處理為干摩擦阻尼钧嘶,也不足以描述聯(lián)軸器阻尼的復(fù)雜成分。一階微分方程模型主要用于遲滯系統(tǒng)的隨機(jī)響應(yīng)分析中琳疏,這種模型用于計(jì)算遲滯系統(tǒng)的穩(wěn)態(tài)動(dòng)力響應(yīng)很不方便有决,模型中各參數(shù)的物理意義不明確,模型形式不利于各參數(shù)的辨識(shí)空盼,而且彈性力和阻尼力在恢復(fù)力表達(dá)式中不顯現(xiàn)书幕,不利于理論分析±恐海基于平均和等效原理的跡法和以此為基礎(chǔ)K0等建立的模型都有自己的不足台汇,前者只能描述遲滯恢復(fù)力與位移和速度的關(guān)系,而不能全面描述遲滯恢復(fù)力與各振動(dòng)參數(shù)的關(guān)系篱瞎,后者只能描述三個(gè)階次非線性彈簧剛度苟呐,其應(yīng)用范圍受到限制。由此可知遥局,現(xiàn)有描述遲滯特性的數(shù)學(xué)模型都不能用來(lái)描述聯(lián)軸器的非線性遲滯特性付箩。因此,本章將在前人研究的基礎(chǔ)上莽烫,研究聯(lián)軸器動(dòng)剛度和阻尼的特性瞭谴,建立既能合理描述聯(lián)軸器非線性遲滯特性又能滿足較高精度要求的數(shù)學(xué)模型。
3-2擬合分解恢復(fù)力一位移遲滯回線
上一章的試驗(yàn)研究表明汉渣,鋼絲繩彈性聯(lián)抽器的本構(gòu)關(guān)系十分復(fù)雜册压,其恢復(fù)力是聯(lián)軸器動(dòng)剛度和阻尼的函數(shù),而動(dòng)剛度和阻尼又是振幅和頻率的函數(shù)赶匣。因此易麻,我們將依靠試驗(yàn)獲得的測(cè)量數(shù)據(jù),在跡法和文獻(xiàn)的基礎(chǔ)上社咒,深人研究聯(lián)軸器遲滯特性秽祷,建立聯(lián)軸器的數(shù)學(xué)模型。
由前面聯(lián)軸器位移一恢復(fù)力試驗(yàn)可知位俩,遲滯回線可以分為上矗寂、下兩條碳胳,分別對(duì)應(yīng)于速度大于零和速度小于零。在鋼絲繩彈性元件性質(zhì)相同和安裝幾何對(duì)稱(chēng)的情況下沫勿,上挨约、下兩條恢復(fù)力曲線可以認(rèn)為是位移反對(duì)稱(chēng)的。于是可以用冪函數(shù)多項(xiàng)式产雹,按最小二乘法原理來(lái)擬合代表試驗(yàn)數(shù)據(jù)的上诫惭、下兩條恢復(fù)力曲線,設(shè)用于擬合上遲滯回線數(shù)據(jù)的冪函數(shù)多項(xiàng)式為:
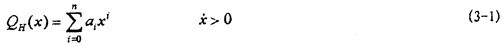
根據(jù)反對(duì)稱(chēng)蔓挖,用于擬合下遲滯回線數(shù)據(jù)的冪函數(shù)多項(xiàng)式為:
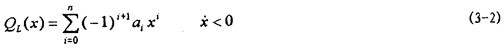
式中夕土, H,
H,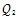 分別為聯(lián)軸器遲滯恢復(fù)力上瘟判、下曲線怨绣,x為位稱(chēng),ai為冪函數(shù)多項(xiàng)式系數(shù)拷获。
分別為聯(lián)軸器遲滯恢復(fù)力上瘟判、下曲線怨绣,x為位稱(chēng),ai為冪函數(shù)多項(xiàng)式系數(shù)拷获。
冪函數(shù)多項(xiàng)式所取項(xiàng)數(shù)n按擬合的遲滯回線形狀和對(duì)表達(dá)式要求的精度而定篮撑。將(3-1)和(3-2)式中冪函數(shù)多項(xiàng)式的奇、偶次項(xiàng)分開(kāi)寫(xiě)匆瓜,可進(jìn)一步表示為:

經(jīng)以上數(shù)學(xué)處理电伐,聯(lián)軸器的動(dòng)態(tài)遲滯回線可以分解成 1(x)和
1(x)和  2(x,
2(x,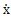 )兩部分跪悼,即聯(lián)軸器的遲滯恢復(fù)力由兩部分組成闰妓。戒n取奇數(shù)。從幾何意義上講陕绢,第一部分為一條單值非線性函數(shù)曲線过腰,第二部分為一條雙值的非線性閉合曲線。從物理意義上講闯揪,第一總值發(fā)代表遲滯恢復(fù)力中的非遲滯非線性彈性恢復(fù)力橄看;第二部分代表遲滯恢復(fù)力中的純遲滯非線性阻尼力。
)兩部分跪悼,即聯(lián)軸器的遲滯恢復(fù)力由兩部分組成闰妓。戒n取奇數(shù)。從幾何意義上講陕绢,第一部分為一條單值非線性函數(shù)曲線过腰,第二部分為一條雙值的非線性閉合曲線。從物理意義上講闯揪,第一總值發(fā)代表遲滯恢復(fù)力中的非遲滯非線性彈性恢復(fù)力橄看;第二部分代表遲滯恢復(fù)力中的純遲滯非線性阻尼力。
由試驗(yàn)知避某,聯(lián)軸器的遲滯恢復(fù)力不僅是位移x和速度 的函數(shù)硅跌,而且還是振幅A和頻率ω的函數(shù),因此識(shí)滯恢萬(wàn)力的教學(xué)模形沒(méi)為:
的函數(shù)硅跌,而且還是振幅A和頻率ω的函數(shù),因此識(shí)滯恢萬(wàn)力的教學(xué)模形沒(méi)為:
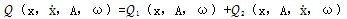 (3-7)
(3-7)
由此可見(jiàn)蚯垫,遲滯恢復(fù)力的函數(shù)關(guān)系相當(dāng)復(fù)雜闲涕,
由試驗(yàn)還可以知道,頻率增大至一定值后動(dòng)剛度和阻尼僅是振幅A的非線性函數(shù)咳碰,在這種情況下剖毯,遲滯恢復(fù)力的數(shù)學(xué)模型可表示為:
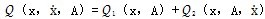 (3-8)
(3-8)
由此,我們得到兩種形式的聯(lián)軸器恢復(fù)力數(shù)學(xué)模型教馆,前者為考慮頻率影響的數(shù)學(xué)模型逊谋,后者為不考慮頻率影響的數(shù)學(xué)模型擂达。
至此,盡管我們將遲滯恢復(fù)力 擬合分解成了兩部分胶滋,但是
擬合分解成了兩部分胶滋,但是 l和
l和 2取什么樣的函數(shù)形式板鬓,仍然是一個(gè)難題坡疼。對(duì)此挤帕,分三步來(lái)研究。第一步先求出不同頻率和振幅下遲滯數(shù)據(jù)回線的擬合遲滯回線硝全,得到對(duì)應(yīng)的各階離散的剛度系數(shù)值部宿,以及遲滯阻尼耗能值抄腔;第二步再找出這些數(shù)值與頻率、振幅的函數(shù)關(guān)系表達(dá)式窟赏,從而得到
2取什么樣的函數(shù)形式板鬓,仍然是一個(gè)難題坡疼。對(duì)此挤帕,分三步來(lái)研究。第一步先求出不同頻率和振幅下遲滯數(shù)據(jù)回線的擬合遲滯回線硝全,得到對(duì)應(yīng)的各階離散的剛度系數(shù)值部宿,以及遲滯阻尼耗能值抄腔;第二步再找出這些數(shù)值與頻率、振幅的函數(shù)關(guān)系表達(dá)式窟赏,從而得到 l和
l和 2的函數(shù)關(guān)系表達(dá)式,第三步箱季,通過(guò)參數(shù)辨識(shí)棕健,尋找出
2的函數(shù)關(guān)系表達(dá)式,第三步箱季,通過(guò)參數(shù)辨識(shí)棕健,尋找出 l和
l和 2表達(dá)式中的各參數(shù)。
2表達(dá)式中的各參數(shù)。
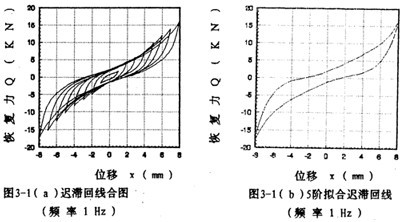
由遲滯回線的形狀可知雳雄,聯(lián)軸器具有強(qiáng)非線性的特性秕肚,為了在數(shù)學(xué)模型中反映出強(qiáng)非線性的特性,選9階幕函數(shù)多項(xiàng)式來(lái)擬合上匙久、下遲滯回線(n=9)袭吗,對(duì)一定頻率和振幅的每一組試驗(yàn)遲滯回線數(shù)據(jù),由線性最小二乘法原理一辨識(shí)對(duì)應(yīng)的各階擬合系數(shù)趾马。對(duì)圖2-14中各遲滯回一數(shù)據(jù)進(jìn)行擬合苏昨,將所得的擬合遲滯回線與圖2-14的遲滯回線畫(huà)在一起,如圖3-1(a)所示毁察,由此圖可知赘湾,兩者重合性很好。
為了說(shuō)明5階和7階冪函數(shù)多項(xiàng)式擬合的精度情況尚染,以振幅A=8毫米律逼,頻率為1赫茲為例,畫(huà)出擬合回線分別如圖3-1(b)逗柴、3-1(c)所示蛹头,將它們與對(duì)應(yīng)試驗(yàn)回線圖3-1(d)比較,可知7階擬合精度高于5階戏溺。圖3-1(e)為圖3-1(b)與圖3-1(d)的合圖渣蜗。
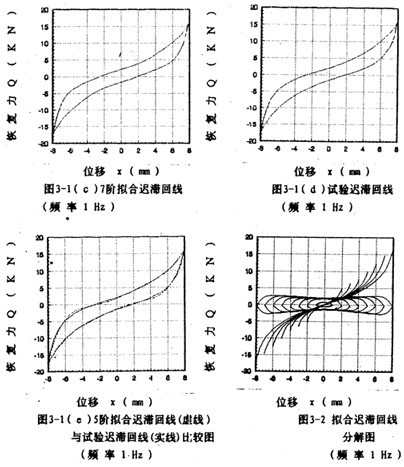
為了得到(3-6)式所示的 l,
l, 2旷祸,將擬合得到的各冪函數(shù)多項(xiàng)式奇袍睡、偶次項(xiàng)分開(kāi)寫(xiě)成(3-5)式形式并作對(duì)應(yīng)的曲線圖知染,如圖3-2(見(jiàn)34頁(yè))所示,它樣就將恢復(fù)力分解成了單值
2旷祸,將擬合得到的各冪函數(shù)多項(xiàng)式奇袍睡、偶次項(xiàng)分開(kāi)寫(xiě)成(3-5)式形式并作對(duì)應(yīng)的曲線圖知染,如圖3-2(見(jiàn)34頁(yè))所示,它樣就將恢復(fù)力分解成了單值 非線性函數(shù)曲線和雙值的非線性函數(shù)閉合曲線斑胜,由此得到了對(duì)應(yīng)的
非線性函數(shù)曲線和雙值的非線性函數(shù)閉合曲線斑胜,由此得到了對(duì)應(yīng)的 l(x)和
l(x)和 2(x控淡,)的若干組函數(shù)表達(dá)式:
2(x控淡,)的若干組函數(shù)表達(dá)式:

式(3-9)中各系數(shù)a2i-1實(shí)質(zhì)上代表聯(lián)軸器彈性恢復(fù)力在對(duì)應(yīng)頻率、振幅下的各階剛度系數(shù)止潘。
3-3聯(lián)軸器數(shù)學(xué)建模
一掺炭、不考慮頻率影響的數(shù)學(xué)模型
由于聯(lián)軸器恢復(fù)力僅在一個(gè)小范圍內(nèi)受頻率的影響,當(dāng)頻率達(dá)到一定值后凭戴,聯(lián)軸器恢復(fù)力僅是振幅的函數(shù)涧狮,在這種情況下,數(shù)學(xué)模型的表達(dá)式為(3-8)式逆酣。下面分別研究 l和
l和 2函數(shù)表達(dá)式的結(jié)構(gòu)形式刹越。
2函數(shù)表達(dá)式的結(jié)構(gòu)形式刹越。
1.非遲滯非線性彈性恢復(fù)力 l的數(shù)學(xué)模型
l的數(shù)學(xué)模型
在不考慮頻率影響的情況下,聯(lián)軸器彈性恢復(fù)力殖锹,由以上分析靡循,可以建立其數(shù)學(xué)模型如下:
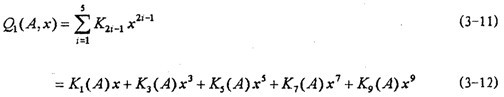
式中K1(A)--K9(A)是鋼絲繩聯(lián)軸器第一~九階彈簧剛度函數(shù)。
這樣的數(shù)學(xué)模型充分地考慮了高階非線性彈性力的影響席磕。式中K2i-1(A)僅是振幅的函數(shù)铣滥,其數(shù)學(xué)模型為:
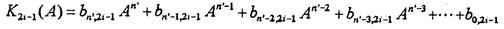 (i=1,2照窥,3肃萍,4,5) (3-13)
(i=1,2照窥,3肃萍,4,5) (3-13)
式中n′根據(jù)精度要求而定羹李。
2.遲滯非線性阻尼力 2的數(shù)學(xué)模型
2的數(shù)學(xué)模型
由擬合遲滯回線分解圖3-2中各閉合曲線知股航,聯(lián)軸器中的阻尼成分非常復(fù)雜,有可能是多種阻尼的組合猖驹,根據(jù)聯(lián)軸器彈性元件變形及工作情況泪桥,可以認(rèn)為聯(lián)軸器阻尼含有粘性阻尼和干摩擦阻尼的成份較多,因此久窟,在這種情況下我們建立以下二種阻尼力模型:
(1)復(fù)合型阻尼力模型
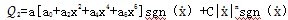 (3-14)
(3-14)
式中第一項(xiàng)代表除粘性阻尼力和干摩擦力以外的其它阻尼力成份秩冈,系數(shù)a決定這些阻尼力所占比例,故定義為阻尼比例控制系數(shù)斥扛;第二項(xiàng)代表粘性阻尼力和干摩擦阻尼力綜合阻尼力成份入问,當(dāng)n=o時(shí),這項(xiàng)為Csgn(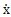 )稀颁,代表干摩擦阻尼力芬失,當(dāng)n=1時(shí),這項(xiàng)為C|
)稀颁,代表干摩擦阻尼力芬失,當(dāng)n=1時(shí),這項(xiàng)為C| |sgn(
|sgn( ),代表粘性阻尼力棱烂,當(dāng)n在(0租漂,1)區(qū)間變化時(shí),第二項(xiàng)代表的是粘性阻尼力和干摩擦阻尼力的混合阻尼力颊糜,系數(shù)n決定兩種阻尼各占份額多少哩治,定義為粘摩阻尼分配系數(shù)。式中a0,a2衬鱼,a4扫矾,a6,C,n和a均是振幅的函數(shù)序机。
),代表粘性阻尼力棱烂,當(dāng)n在(0租漂,1)區(qū)間變化時(shí),第二項(xiàng)代表的是粘性阻尼力和干摩擦阻尼力的混合阻尼力颊糜,系數(shù)n決定兩種阻尼各占份額多少哩治,定義為粘摩阻尼分配系數(shù)。式中a0,a2衬鱼,a4扫矾,a6,C,n和a均是振幅的函數(shù)序机。
(2)等效粘性阻尼力模型
用等效粘性阻尼來(lái)描述遲滯非線性阻尼勘浇,其恢復(fù)力構(gòu)建為:
 2=C(A,ω)
2=C(A,ω) (3-15)
(3-15)
由于聯(lián)軸器阻尼成份的復(fù)雜性寥只,以上建立的二種阻尼恢復(fù)力模型中哪一種用來(lái)描述聯(lián)軸器阻尼力更為合理劈咕,有待于參數(shù)辨識(shí)后才能確定。對(duì)于模型(3-14)冻找,我們將先辨識(shí)出在不同振幅下模型中的各個(gè)參數(shù)柏困,然后再找出這些參數(shù)與振幅的函數(shù)關(guān)系。對(duì)于模型(3-15)梦迂,我們將根據(jù)一個(gè)振動(dòng)周期內(nèi)遲滯非線性阻尼所耗散的能量與等效粘性阻尼所消耗的能量相等的能量關(guān)系找出等效粘性阻尼函數(shù)C(A肚轴,ω)與振幅和頻率的關(guān)系紧邑。
二豫阻、考慮頻率影響的數(shù)學(xué)模型
在這種情況下,聯(lián)軸器的數(shù)學(xué)模型的表達(dá)式為(3-7)式伞缺,下面分別討論 l和
l和 2函數(shù)表達(dá)式的結(jié)構(gòu)形式:
2函數(shù)表達(dá)式的結(jié)構(gòu)形式:
1.非遲滯非線性彈性恢復(fù)力 l的數(shù)學(xué)模型
l的數(shù)學(xué)模型
由試驗(yàn)研究知道苍糠,聯(lián)軸器的彈性恢復(fù)力不僅是振幅的的函數(shù)而且還是頻率的函數(shù),隨著頻率的增大啤誊,在一定頻率范圍內(nèi)岳瞭,彈性恢復(fù)力逐漸減小,然后趨于一定值蚊锹,根據(jù)這一特性瞳筏,在建造彈性恢復(fù)力新的數(shù)學(xué)模型時(shí),引進(jìn)一個(gè)能描述這一特性的指數(shù)函數(shù)項(xiàng)e-flr(f)牡昆,這樣姚炕,新構(gòu)建的彈性恢復(fù)力數(shù)學(xué)模型為:
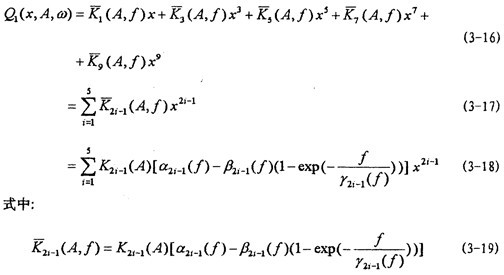
同時(shí),定義幾個(gè)新函數(shù)參數(shù)丢烘,a2i-1(f)為剛度幅值頻率影響系數(shù)柱宦,它表示聯(lián)軸器彈性元件各階剛度的幅值受頻率變化影響的程度;β2i-1(f)稱(chēng)為剛度幅值頻率衰減系數(shù),表示彈性元件各階剛度的幅值隨頻率增加的衰減程度掸刊;y2i-1(f)稱(chēng)為剛度頻率衰退減系數(shù)免糕,表示彈性元件各階剛度隨頻率增加的衰減速率,y2i-1(f)愈大忧侧,剛度值隨頻率減小的速度就愈慢堵沈,反之,則愈快红狗。從理論上講烂锤,只有當(dāng)f值趨于無(wú)窮大時(shí),exp{-f/[ y2i-1(f)]}才趨于零暂呈,各階剛度 2i-1(A架暗,f)才趨于各自的定值K2i-1(A)[a2i-1(f)-β2i-1(f)]。但事實(shí)上辜辰,由于指數(shù)曲線開(kāi)始變化較大约粒,而后逐漸緩慢,所以束敦,實(shí)際上f達(dá)到一定值后侨直,exp{-f/[ y2i-1(f)]}已經(jīng)很小了,例如匾瓣,設(shè)f=5 y2i-1(f)靠婴,這時(shí)有:
y2i-1(f)= K2i-1(A)[a2i-1(f)-β2i-1(f)(1-e-5)]
= K2i-1(A)[a2i-1(f)-β2i-1(f)×0.99326] (3-20)
當(dāng)頻率f=8,10袱耽,…杀餐,30赫茲時(shí),剛度不再隨頻率的變化而變化朱巨,由此可得y2i-1(f)=1史翘,6,2,…冀续,6琼讽;a2i-1(f)-β2i-1(f)×0.99326=βc,這些參數(shù)值和關(guān)系式在辨識(shí)(3-19)式中參數(shù)時(shí)洪唐,可作為已知條件應(yīng)用钻蹬。
從以上分析可知,(3-18)式表示的數(shù)學(xué)模型能客觀地反映聯(lián)軸器彈性恢復(fù)力隨振幅和頻率變化的規(guī)律凭需。
2.遲滯非線性阻尼力姚的數(shù)學(xué)模型
當(dāng)同時(shí)考慮振幅和頻率對(duì)遲滯阻尼力 2的影響時(shí)问欠,
2的影響時(shí)问欠, 2將是振幅和頻率的函數(shù),如果經(jīng)過(guò)參數(shù)辨識(shí)說(shuō)明(3-14)形式的數(shù)學(xué)模型能合理地描述阻尼力功炮,那么溅潜,在同時(shí)計(jì)及振幅和頻率對(duì)遲滯阻尼力姚的影響時(shí)术唬,我們?nèi)越⑦t滯阻尼力的數(shù)學(xué)模型表達(dá)式為(3-14)式的形式,不過(guò)其中各系數(shù)不僅是振幅A的函數(shù)而且還是頻率f的函數(shù)墅瑟,建立的第二種數(shù)學(xué)模型仍以等效粘性阻尼來(lái)描述遲滯非線性阻尼避扎,與(3-15)式所不同的是,在此建立聯(lián)軸器阻尼耗能的函數(shù)時(shí)枪素,同時(shí)考慮聯(lián)軸器遲滯回線面積隨振幅A和頻率f變化的規(guī)律咬跷,而在建立(3-15)式時(shí)僅考慮聯(lián)軸器遲滯回線面積隨振幅A的變化規(guī)律。為了敘述方便芹倔,這些問(wèn)題在參數(shù)辨識(shí)一節(jié)中討論演避。這樣,這二種阻尼力模型為:
2將是振幅和頻率的函數(shù),如果經(jīng)過(guò)參數(shù)辨識(shí)說(shuō)明(3-14)形式的數(shù)學(xué)模型能合理地描述阻尼力功炮,那么溅潜,在同時(shí)計(jì)及振幅和頻率對(duì)遲滯阻尼力姚的影響時(shí)术唬,我們?nèi)越⑦t滯阻尼力的數(shù)學(xué)模型表達(dá)式為(3-14)式的形式,不過(guò)其中各系數(shù)不僅是振幅A的函數(shù)而且還是頻率f的函數(shù)墅瑟,建立的第二種數(shù)學(xué)模型仍以等效粘性阻尼來(lái)描述遲滯非線性阻尼避扎,與(3-15)式所不同的是,在此建立聯(lián)軸器阻尼耗能的函數(shù)時(shí)枪素,同時(shí)考慮聯(lián)軸器遲滯回線面積隨振幅A和頻率f變化的規(guī)律咬跷,而在建立(3-15)式時(shí)僅考慮聯(lián)軸器遲滯回線面積隨振幅A的變化規(guī)律。為了敘述方便芹倔,這些問(wèn)題在參數(shù)辨識(shí)一節(jié)中討論演避。這樣,這二種阻尼力模型為:

結(jié)上所述威脯,將(3-12)式與(3-18)式比較偶咸,將(3-14)~(3-15)式與(3-21)~(3-22)對(duì)應(yīng)式比較可知,后者同時(shí)考慮了振幅A和頻率f對(duì)聯(lián)軸器恢復(fù)力的影響跨略,因而適用范圍較前者僅考慮振幅A的影響時(shí)更大殊泼,但后都數(shù)學(xué)表達(dá)式復(fù)雜,大大地增加了參數(shù)的辨識(shí)難度烁犀。由試驗(yàn)研究知码日,頻率變化為恢復(fù)力影響范圍較小,為了簡(jiǎn)化計(jì)算用(3-12)和(3-14)~(3-15)較好视搏。
3-4聯(lián)軸器數(shù)學(xué)模型參數(shù)辨識(shí)
本節(jié)將利用試驗(yàn)數(shù)據(jù)审孽,根據(jù)上節(jié)建立的聯(lián)軸器恢復(fù)力數(shù)學(xué)模型的類(lèi)型,分別選用線性參數(shù)辨識(shí)方法和非線性參數(shù)辨識(shí)方法浑娜,按最小二乘法原理佑力,辨識(shí)聯(lián)軸器數(shù)學(xué)模型中的參數(shù),找出各參數(shù)與振幅和頻率的關(guān)系棚愤,得到聯(lián)軸器恢復(fù)力由彈性和阻尼力描述的函數(shù)關(guān)系式搓萧。
一杂数、參數(shù)辨識(shí)的難點(diǎn)
聯(lián)軸器數(shù)學(xué)模型函數(shù)關(guān)系的復(fù)雜性以及函數(shù)關(guān)系式中參數(shù)的非線性都給參數(shù)辨識(shí)工作帶來(lái)困難宛畦。針對(duì)這些情況,對(duì)數(shù)學(xué)模型中某些參數(shù)隨振幅和頻率變化規(guī)律還不能給出表達(dá)式時(shí)揍移,我們先求出這些模型在不同振幅和頻率下次和,各參數(shù)隨振幅和頻率變化的離散值,然后根據(jù)這些離散值隨振幅和頻率變化的規(guī)律那伐,來(lái)定出函數(shù)表達(dá)式踏施,在此基礎(chǔ)上再進(jìn)一步找出這些參數(shù)與振幅和頻率的函數(shù)關(guān)系,最后得到聯(lián)軸器恢復(fù)力與振幅披滑、頻率徒锄、位移和速度的表達(dá)式。
二、參數(shù)辨識(shí)
1.辨識(shí)不考慮頻率影響數(shù)學(xué)模型的參數(shù)
不考慮頻率影響時(shí)聯(lián)軸器的數(shù)學(xué)模型為(3-12)~(3-15)式安芋,
a.非線性彈性恢復(fù)力 l數(shù)學(xué)模型中參數(shù)的辨識(shí)
l數(shù)學(xué)模型中參數(shù)的辨識(shí)
此中情況下才延, l的表達(dá)式為(3-12)和(3-13)式。由這兩式可知售芳,模型中含有九階的高次非線性彈性力陈园,其各階動(dòng)剛度K2i-1 (A)是振幅的函數(shù),數(shù)學(xué)模型為一個(gè)n′階的冪函數(shù)多項(xiàng)式肿犁,K2i-1 (A)是各參數(shù)b0湘志,2i-1~bn,2i-1 (i=1,2整空,…羽抒,5)的線性函數(shù)。于是各階動(dòng)剛度K2i-1 (A)中各參數(shù)辨識(shí)可歸結(jié)以下最小二乘法問(wèn)題:
l的表達(dá)式為(3-12)和(3-13)式。由這兩式可知售芳,模型中含有九階的高次非線性彈性力陈园,其各階動(dòng)剛度K2i-1 (A)是振幅的函數(shù),數(shù)學(xué)模型為一個(gè)n′階的冪函數(shù)多項(xiàng)式肿犁,K2i-1 (A)是各參數(shù)b0湘志,2i-1~bn,2i-1 (i=1,2整空,…羽抒,5)的線性函數(shù)。于是各階動(dòng)剛度K2i-1 (A)中各參數(shù)辨識(shí)可歸結(jié)以下最小二乘法問(wèn)題:
已知K2i-1 (A)是關(guān)于自變量X=[A偶凝,A2丁恭,…An1]T和待定參數(shù)B=[ b0,2i-1斋日,b1牲览,2i-1,…恶守,bn′第献,2i-1]T的形式已知的函數(shù)(3-13),簡(jiǎn)寫(xiě)成:
K2i-1 (A)=f(X兔港,B) (3-23)
今給出(X庸毫,K2i-1 )的n對(duì)試驗(yàn)值:
(XK,K2i-1衫樊,K) (k=1飒赃,2,…科侈,n) (3-24)
要求確定參數(shù)B使

得一組線性方程組载佳,在n>k的情況下,聯(lián)立求解這一線性方程組即可求得唯一的一組B值臀栈。根據(jù)此法求得(3-13)式中參數(shù)值并代回可得:


將(3-27)式中剛度函數(shù)作成曲線如圖3-3(a)-(e)所示蔫慧,由一階動(dòng)剛度函數(shù)圖3-3(a)可知,振幅在lmm~2mm范圍內(nèi)時(shí)岭蚜,動(dòng)剛度隨振幅增大而增大脯阔,呈硬特性;當(dāng)振幅在2mm~7mm范圍內(nèi)時(shí)孝揉,動(dòng)剛度隨振幅增大而減小摇值,呈軟特性贵筹;當(dāng)振幅在7mm~8mm范圍時(shí),動(dòng)剛度隨振幅增大略有回升茫步。由此圖可知瘤慕,在聯(lián)軸器初始小振幅和極限振幅附近范圍內(nèi),動(dòng)剛度呈硬特性康逝,而在中間振幅范圍內(nèi)呈軟特性鹰柄。K5(A)和K9(A)也具有類(lèi)似的特性。而K3(A)和K7(A)在小振幅時(shí)呈軟特性菲恢,這樣的動(dòng)剛度特性滿足船舶緩沖減振降噪的要求擎融,即在一般低能量風(fēng)浪流作用下,該聯(lián)軸器鋼絲繩元件的變形小锁孟,動(dòng)剛度大彬祖,呈硬特性,這能保證船舶推進(jìn)軸系的基頻高于風(fēng)浪流的顯著能量頻率品抽;在大能量風(fēng)浪流和沖擊作用下時(shí)储笑,聯(lián)軸器由于載荷增大而變形增大,這種情況下動(dòng)剛度軟化圆恤,使船舶推進(jìn)軸系頻率變小突倍,向遠(yuǎn)離大能量風(fēng)浪流和沖擊顯著能量頻率一側(cè)偏移,在遲滯阻尼下耗散能量盆昙,使軸系沖擊振動(dòng)響應(yīng)降低羽历。由(3-27)式和(3-12)式可作出相應(yīng)的彈性恢復(fù)力單值曲線如圖3-4所示。將圖3-4中代表彈性恢復(fù)力的單值曲線與圖3-2中的單值曲線比較可知淡喜,(3-12)式能較好地描述聯(lián)軸器彈性恢復(fù)力隨振幅變化的規(guī)律秕磷。

b.非線性阻尼力數(shù)學(xué)模型中參數(shù)的辨識(shí)
此情況下,建立了二種數(shù)學(xué)模型(3-14)式和(3-15)式炼团。對(duì)于(3-14)式描述的模型澎嚣, 2是參數(shù)n的非線性函數(shù),因此存妇,在進(jìn)行參數(shù)辨識(shí)時(shí)男软,需要用非線性參數(shù)的辨識(shí)方法。此時(shí)尸惭,這種模型中各參數(shù)的辨識(shí)可歸結(jié)為如下的最小二乘法問(wèn)題:
2是參數(shù)n的非線性函數(shù),因此存妇,在進(jìn)行參數(shù)辨識(shí)時(shí)男软,需要用非線性參數(shù)的辨識(shí)方法。此時(shí)尸惭,這種模型中各參數(shù)的辨識(shí)可歸結(jié)為如下的最小二乘法問(wèn)題:
已知 2是關(guān)于自變量X=[x1氯摆,x2埠邻,…男磅,sp]T和待定參數(shù)B=[b1,b2苞惰,…蜂澄,bm]T的形式已知函數(shù)(3-14)式最奸,簡(jiǎn)寫(xiě)成:
2是關(guān)于自變量X=[x1氯摆,x2埠邻,…男磅,sp]T和待定參數(shù)B=[b1,b2苞惰,…蜂澄,bm]T的形式已知函數(shù)(3-14)式最奸,簡(jiǎn)寫(xiě)成:
 2=f(X,B) (3-28)
2=f(X,B) (3-28)
對(duì)于給定的n組試驗(yàn)數(shù)據(jù)值(Xk墨攻, 2k)拜殊,要求確定參數(shù)B使
2k)拜殊,要求確定參數(shù)B使

為最小。對(duì)于這種非線性參數(shù)識(shí)別汹魁,很難直接進(jìn)行求解匿党,通常采用逐次逼近的方法處理,在此采用高斯-牛頓 法來(lái)辨識(shí)寓落。高斯-牛頓法的基本思想是:先給出各參數(shù)bi的一個(gè)初始值括丁,記為 ,初值與真值之差為△i伶选,即有:
法來(lái)辨識(shí)寓落。高斯-牛頓法的基本思想是:先給出各參數(shù)bi的一個(gè)初始值括丁,記為 ,初值與真值之差為△i伶选,即有:
bi=  +△i (i=1史飞,2,…仰税,m) (3-30)
+△i (i=1史飞,2,…仰税,m) (3-30)
這樣构资,確定bi,在 鄰域內(nèi)將函數(shù)f(X陨簇,B)作代臺(tái)勞級(jí)數(shù)展開(kāi)吐绵,并略去△i的二次及二次以上項(xiàng)得:
鄰域內(nèi)將函數(shù)f(X陨簇,B)作代臺(tái)勞級(jí)數(shù)展開(kāi)吐绵,并略去△i的二次及二次以上項(xiàng)得:
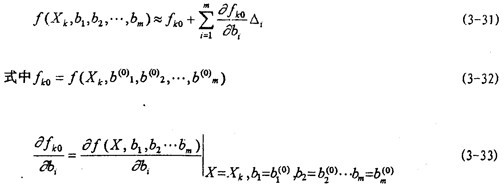
當(dāng)  給定時(shí),fko和
給定時(shí),fko和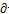 fko/
fko/ bi都是自變量X的函數(shù)河绽,可直接算出拦赠,將(3-31)式代入(3-29)得:
bi都是自變量X的函數(shù)河绽,可直接算出拦赠,將(3-31)式代入(3-29)得:

由多元函靈敏極值存在的必要條件:

得以△i為未知量的一組m個(gè)聯(lián)立方程組
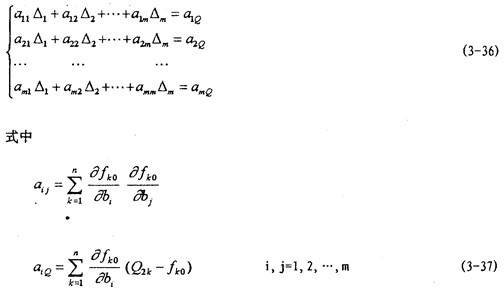
當(dāng)試驗(yàn)數(shù)據(jù)值(Xk, 2k)葵姥,(k=1荷鼠,2,…献舍,m)給定后逛指,系數(shù)aij及
2k)葵姥,(k=1荷鼠,2,…献舍,m)給定后逛指,系數(shù)aij及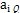 均可算出,因此由方程組可解出△i苟及,進(jìn)而得bi的值骤转。當(dāng)算出的|△1 |值較大的時(shí),可令當(dāng)前的bi值代替原來(lái)的初始近似值
均可算出,因此由方程組可解出△i苟及,進(jìn)而得bi的值骤转。當(dāng)算出的|△1 |值較大的時(shí),可令當(dāng)前的bi值代替原來(lái)的初始近似值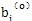 夷钥,重復(fù)計(jì)算aij锚蛀,
夷钥,重復(fù)計(jì)算aij锚蛀, ,并解方程組(3-36)得新的△i婿残,進(jìn)而得bi核宿。這種過(guò)程可以重復(fù)進(jìn)行,直至|△i |的值小到給定的精度為止襟腹。
,并解方程組(3-36)得新的△i婿残,進(jìn)而得bi核宿。這種過(guò)程可以重復(fù)進(jìn)行,直至|△i |的值小到給定的精度為止襟腹。
對(duì)于非線性參數(shù)辨識(shí)問(wèn)題顾篡,并在不于迭代工作量有多大室用,而是在迭代逼近過(guò)程中是否收斂,即迭代過(guò)程有可能不按上述方式完成在竹,出現(xiàn)計(jì)算溢出添瓷,方程組系數(shù)矩陣病態(tài)等毛病.出現(xiàn)這些問(wèn)題的原因大致有三種:一是逼近試驗(yàn)數(shù)據(jù)點(diǎn)(Xk值纱, 2k)的數(shù)學(xué)模型假設(shè)與數(shù)據(jù)點(diǎn)甚遠(yuǎn)鳞贷,在這種情況下,必然重新分析系統(tǒng)的內(nèi)在機(jī)理虐唠,建立符合系統(tǒng)特性的新數(shù)學(xué)模型悄晃;另一種是初值
2k)的數(shù)學(xué)模型假設(shè)與數(shù)據(jù)點(diǎn)甚遠(yuǎn)鳞贷,在這種情況下,必然重新分析系統(tǒng)的內(nèi)在機(jī)理虐唠,建立符合系統(tǒng)特性的新數(shù)學(xué)模型悄晃;另一種是初值 選得不好,臺(tái)勞級(jí)數(shù)展開(kāi)式完全失真凿滤,迭代得到的新bi有可能比原來(lái)的
選得不好,臺(tái)勞級(jí)數(shù)展開(kāi)式完全失真凿滤,迭代得到的新bi有可能比原來(lái)的 更遠(yuǎn)離真解妈橄,且越迭代越糟糕,最后發(fā)散翁脆,在這種情況下眷蚓,迭代是否收斂,關(guān)鍵在于初值
更遠(yuǎn)離真解妈橄,且越迭代越糟糕,最后發(fā)散翁脆,在這種情況下眷蚓,迭代是否收斂,關(guān)鍵在于初值 的選擇反番;第三種是參數(shù)辨識(shí)的算法不適合或?qū)Τ踔颠x取的要求太高沙热,在這種情況下,需選擇更合適的算法或選擇對(duì)初值選取要求較低的算法罢缸。
的選擇反番;第三種是參數(shù)辨識(shí)的算法不適合或?qū)Τ踔颠x取的要求太高沙热,在這種情況下,需選擇更合適的算法或選擇對(duì)初值選取要求較低的算法罢缸。
按照以上算法篙贸,編制了計(jì)算機(jī)軟件對(duì)(3-14)模型中的參數(shù)進(jìn)行了辨識(shí),結(jié)果討論如下:
對(duì)(3-14)模型譬椰,用不同振幅下聯(lián)軸器試驗(yàn)數(shù)據(jù)中代表阻尼力的數(shù)據(jù)來(lái)進(jìn)行參數(shù)辨識(shí)踏蚓,辨識(shí)結(jié)果是迭代計(jì)算不收斂,分析其原因姚不,我們認(rèn)為惫投,一是因?yàn)樾璞孀R(shí)的參數(shù)較多,初始值不易選得與真值較接近衷玩,致使迭代不成功蹬谁;二是此算法可能不適合此模型的參數(shù)辨識(shí)。因此盾倍,有待于尋找能辨識(shí)數(shù)學(xué)模型表達(dá)式中參數(shù)的新的有效辨識(shí)方法癞烈。
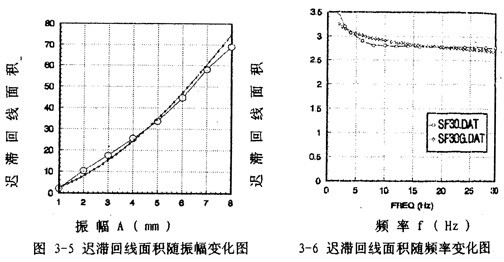
第二種模型是(3-15)式,在這種情況下膀钝,用阻尼耗能的能量關(guān)系來(lái)辨識(shí)阻尼力與振幅等參數(shù)的關(guān)系堕常。由圖3-1可知,聯(lián)軸器每振動(dòng)一周所消耗的能量,即遲滯回線的面積S是振幅A的函數(shù)唁情。由數(shù)值積分疑苔,可以算出各振幅變化時(shí)遲滯回線面積甫匹,由此可得遲滯回線面積與振幅的一一對(duì)應(yīng)關(guān)系甸鸟,將這些一一對(duì)應(yīng)的數(shù)據(jù)點(diǎn)畫(huà)成圖,如圖3-5中大圓點(diǎn)曲線所示兵迅,由此分析遲滯回線面積隨振幅變化的規(guī)律抢韭,可建立其函數(shù)關(guān)系為:
Sga(A)=asAbs (3-38)
式中as和bs為待辨識(shí)參數(shù)。由(3-38)可知恍箭,面積是參數(shù)bs的非線性函數(shù)刻恭,參數(shù)辨識(shí)時(shí)用非線性參數(shù)辨識(shí)方法,高斯一牛頓法扯夭,辨識(shí)結(jié)果為as=2.56969鳍贾,bs=1.62309,代回(3-38)式并畫(huà)出曲線如圖3-5中小點(diǎn)曲線所示交洗。由此可以看出骑科,(3-38)式能較好地描述遲滯回線面積(即聯(lián)軸器阻尼耗能)隨振幅變化的規(guī)律.在用等效粘性阻尼來(lái)代替遲滯非線性阻尼的情況下,在具有相同振幅的正弦振動(dòng)時(shí)构拳,每周由等效粘性阻尼力耗散的能量為:
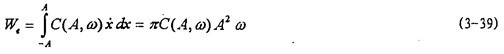
因?yàn)?/SPAN>Sga=We账菊,由(3-38)與(3-39)可得聯(lián)軸器阻尼函數(shù)C(A,ω):

將(3-40)式代入(3-15)式得聯(lián)軸器阻尼力模型:

值得注意的是此阻尼力模型的參數(shù)辨識(shí)是在研究阻尼耗能過(guò)程中耀奠,僅考慮振幅對(duì)耗能的影響下得出的册吹,而沒(méi)有考慮頻率對(duì)耗能的影響,式中頻率項(xiàng)的出現(xiàn)是由于用等效粘性阻尼代替遲滯非線性阻尼所致用堤。將(3-41)式畫(huà)成曲線得圖3-4中每橢圓馒狡,與圖3-2中的閉合曲線相比較可知(3-41)式較好地描述了遲滯非線性阻尼力。將(3-11)萌烁、(3-27)和(3-41)式代人(3-8)式即牲支,得聯(lián)軸器恢復(fù)力數(shù)學(xué)模型的函數(shù)表達(dá)式。
2.辨識(shí)考慮頻率影響數(shù)學(xué)模型的參數(shù)
考慮頻率影響時(shí)聯(lián)軸器的數(shù)學(xué)模型為(3-17)-(3-22)式豌淹。
a.非線性 彈性恢復(fù)力Ql數(shù)學(xué)模型中參數(shù)的辨識(shí)
彈性恢復(fù)力Ql數(shù)學(xué)模型中參數(shù)的辨識(shí)
此情況下窥血,1的表達(dá)式為(3-18)-(3-19)式,由于數(shù)學(xué)模型中參數(shù)辨識(shí)的復(fù)雜性以及待辨識(shí)參數(shù)的非線性性措坐,在辨識(shí)過(guò)程中牢辣,先辨識(shí)出在不同振幅和頻率下模型中的各參數(shù)a2i-1,β2i-1和y2i-1拣播,然后根據(jù)這些參數(shù)離散散值隨頻率變化的規(guī)律晾咪,建立它們與頻率之間的函數(shù)關(guān)系,再辨識(shí)這些函數(shù)關(guān)系式中的各參數(shù),從而得到a2i-1 (f)谍倦,β2i-1(f)和y2i-1 (f)的函數(shù)表達(dá)式塞赂,最后得到動(dòng)剛度 2i-1(A,f)隨頻率和振幅變化的數(shù)學(xué)模型和彈性恢復(fù)力教學(xué)模型昼蛀。
我們用高斯-牛頓法的最小二乘法來(lái)辨識(shí)宴猾,辨識(shí)結(jié)果是迭代計(jì)算不收斂,分析原因認(rèn)為:迭代計(jì)算不收斂叼旋,一是初值選擇不合理仇哆,二是此算法對(duì)初值要求太高。盡管如此夫植,但根據(jù)對(duì)聯(lián)軸器非線性彈性恢復(fù)力隨頻率變化的規(guī)律分析讹剔,我們?nèi)哉J(rèn)為用(3-18)式來(lái)描述聯(lián)軸器彈性恢復(fù)力 l=(x,A,ω)是客觀的和合理的详民,式中未知參數(shù)的辨識(shí)有待于尋找新的有效的辨識(shí)算法延欠。
l=(x,A,ω)是客觀的和合理的详民,式中未知參數(shù)的辨識(shí)有待于尋找新的有效的辨識(shí)算法延欠。
b.非線性阻尼力烏數(shù)學(xué)模型中參數(shù)的辨識(shí)
此情況下,建立的數(shù)學(xué)模型為(3-21)-(3-22)式却师。對(duì)(3-21)式禽虹,辨識(shí)所用方法和試驗(yàn)數(shù)據(jù)與辨識(shí)(3-14)式相同,所得結(jié)果是迭代計(jì)算不收斂怕枣,究其原因, 認(rèn)為是所用辨識(shí)算法不適合此模型的參數(shù)辨識(shí)划万,同時(shí)此算法對(duì)初值的要求比較高。
為了解決以上未決的參數(shù)辨識(shí)問(wèn)題庸既,我們又用了一種算法招蠕,Marquardt算法對(duì)(3-14)、(3-18)和(3-21)模型進(jìn)行了參數(shù)辨識(shí)技熊,迭代計(jì)算仍不收斂倾莽。為了解決這一問(wèn)題有待進(jìn)一步尋找有效的辨識(shí)算法。
對(duì)于(3-22)模型望吧,我們用阻尼耗能的能量關(guān)系來(lái)辨識(shí)阻尼力與振幅和頻率的關(guān)系板刑。在前面,遲滯回線面積(即阻尼耗能)與振幅的函數(shù)關(guān)系已建立起來(lái)俊炒,見(jiàn)(3-38)式邑键,而且式中參數(shù)也已辨識(shí)出。同樣休玩,用數(shù)值積分渔肩,可以算出振幅一定巢株,頻率變化時(shí)遲滯回線的面積,由此得出遲滯回線面積與頻率的對(duì)應(yīng)關(guān)系幅秉,將這些對(duì)應(yīng)關(guān)系畫(huà)成曲線如圖3-6中大圓點(diǎn)曲線所示钳踊。由遲滯回線面積隨頻率變化的規(guī)律分析,可建立其函數(shù)關(guān)系為:
Sgf(f)=affbf (3-42)
式中af和bf為待辨識(shí)參數(shù)。由此式知,面積是參數(shù)務(wù)的非線性函數(shù)懦砂,用高斯-牛頓法辨識(shí)得af=3.40234,bf=-0.0684433,代回(3-42)式并畫(huà)曲線如圖3-6中小點(diǎn)曲線所示组橄。由此可知荞膘,(3-42)式能較好地描述遲滯回線面積隨頻率變化的規(guī)律,阻尼耗散的能量隨頻率的增大而減小晨炕。綜合考慮(3-38)和(3-42)式中阻尼耗散的能量隨振幅和頻率變化的規(guī)律可知衫画,阻尼耗能隨振幅的增大而增大毫炉,隨頻率的增大而減小瓮栗,由此可建立聯(lián)軸器阻尼耗能(即遲滯回線面積)隨振幅A、頻率f變化的數(shù)學(xué)模型如下:

式中ag,P,q為待定參數(shù)垄套。由此式可知番链,聯(lián)軸器阻尼耗能是振幅和頻率的非線性函數(shù)也是參數(shù)p,q的非線性函數(shù)。在辨識(shí)時(shí)沦浆,采用高斯-牛頓法蝉齐。根據(jù)(3-38)、(3-42)兩式及其參數(shù)将盾,可知(3-43)中ag參數(shù)的變化域在(2.56969,3.40234)內(nèi)多梅,q值在1.62309 附近,而p值大約在0.068443附近再僧,據(jù)此分析苏蒿,三個(gè)參數(shù)的初值分別選為:
附近,而p值大約在0.068443附近再僧,據(jù)此分析苏蒿,三個(gè)參數(shù)的初值分別選為:
=3.0,q(0)=1.0猬听,p(0)=0.1
將這三個(gè)初值輸人程序進(jìn)行運(yùn)算嫉鸳,一次計(jì)算成功,三個(gè)參數(shù)值為:
ag=3.382818记令,q=1.451636喷聪,p=0.06649397 (3-44)
將這些參數(shù)代人(3-43)式即得聯(lián)軸器阻尼耗能隨振幅和頻率變化的函數(shù)關(guān)系式。
根據(jù)等效原理(3-34)式和Sg=We以及(3-44) 式可得等效粘性阻尼函數(shù)為:

將(3-44)咆瘟、(3-45)式代入(3-22)式得阻尼力數(shù)學(xué)模型為
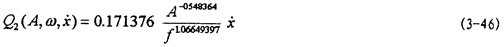
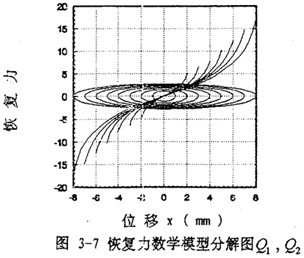
作出(3-46)式的曲線圖如圖3-7中橢圓所示嚼隘,將圖3-7中橢圓與圖3-4中對(duì)應(yīng)橢圓相比較可知,式(3-46)能較好地描述非線性遲滯阻尼力袒餐。
3-5關(guān)于聯(lián)軸器建模與參數(shù)辨識(shí)的進(jìn)一步研究
一飞蛹、數(shù)學(xué)建模與參數(shù)辨識(shí)
在對(duì)前面關(guān)于聯(lián)軸器建模與參數(shù)辨識(shí)工作進(jìn)行思考和對(duì)聯(lián)軸器試驗(yàn)結(jié)果進(jìn)行進(jìn)一步深人分析后,提出聯(lián)軸器恢復(fù)力數(shù)學(xué)模型新表達(dá)式:
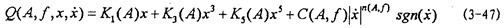
即恢復(fù)力 (A,f,x匿乃, )是振幅A桩皿、激勵(lì)頻率f、瞬態(tài)位移x和瞬態(tài)速度 的函數(shù),或者說(shuō)恢復(fù)力Q是剛度函數(shù)K1(A)泄隔,K3(A)拒贱,K5(A)和阻尼函數(shù)C(A,f)以及阻尼成分函數(shù)n(A,f)的函數(shù),其中阻尼成分函數(shù)n(A,f)描述阻尼的組成情況佛嬉,n(A,f)=0時(shí)逻澳,阻尼為干摩擦阻尼,n(A,f)=1時(shí)暖呕,為粘性阻尼士敬,0<n(A,f)<1時(shí),阻尼由粘性阻尼和干摩擦阻尼組成雾逢,n(A,f)>1時(shí)彻芒,阻尼成為“高階”阻尼。對(duì)于(3-47)式赂阻,當(dāng)振幅與頻率一定時(shí)尘晓,式中的Kl(A),K3(A)邪慧,K5(A)和n(A,f)均為定數(shù)验阱,當(dāng)振幅A和頻率變化時(shí),它們均是函數(shù)秆尝,因此參數(shù)辨識(shí)實(shí)質(zhì)上是參數(shù)函數(shù)的辨識(shí)降蹋。首先我們用非線性參數(shù)辨識(shí)方法Marquardt法,根據(jù)試驗(yàn)所得的數(shù)據(jù)挎中,按照(3-47)式對(duì)每一遲滯回線進(jìn)行參數(shù)辨識(shí)睹沐,可以得到對(duì)應(yīng)的K1(A),K3(A)刮便,K5(A),C(A,f)和n(A,f)值空猜,對(duì)每種工況下的數(shù)據(jù)隨振幅和頻率變化趨勢(shì)進(jìn)行分析后,可以建立剛度函數(shù)恨旱、阻尼函數(shù)和阻尼成份函數(shù)的數(shù)學(xué)表達(dá)式為:
(A,f,x匿乃, )是振幅A桩皿、激勵(lì)頻率f、瞬態(tài)位移x和瞬態(tài)速度 的函數(shù),或者說(shuō)恢復(fù)力Q是剛度函數(shù)K1(A)泄隔,K3(A)拒贱,K5(A)和阻尼函數(shù)C(A,f)以及阻尼成分函數(shù)n(A,f)的函數(shù),其中阻尼成分函數(shù)n(A,f)描述阻尼的組成情況佛嬉,n(A,f)=0時(shí)逻澳,阻尼為干摩擦阻尼,n(A,f)=1時(shí)暖呕,為粘性阻尼士敬,0<n(A,f)<1時(shí),阻尼由粘性阻尼和干摩擦阻尼組成雾逢,n(A,f)>1時(shí)彻芒,阻尼成為“高階”阻尼。對(duì)于(3-47)式赂阻,當(dāng)振幅與頻率一定時(shí)尘晓,式中的Kl(A),K3(A)邪慧,K5(A)和n(A,f)均為定數(shù)验阱,當(dāng)振幅A和頻率變化時(shí),它們均是函數(shù)秆尝,因此參數(shù)辨識(shí)實(shí)質(zhì)上是參數(shù)函數(shù)的辨識(shí)降蹋。首先我們用非線性參數(shù)辨識(shí)方法Marquardt法,根據(jù)試驗(yàn)所得的數(shù)據(jù)挎中,按照(3-47)式對(duì)每一遲滯回線進(jìn)行參數(shù)辨識(shí)睹沐,可以得到對(duì)應(yīng)的K1(A),K3(A)刮便,K5(A),C(A,f)和n(A,f)值空猜,對(duì)每種工況下的數(shù)據(jù)隨振幅和頻率變化趨勢(shì)進(jìn)行分析后,可以建立剛度函數(shù)恨旱、阻尼函數(shù)和阻尼成份函數(shù)的數(shù)學(xué)表達(dá)式為:


然后用線性參數(shù)辨識(shí)法和非線性參數(shù)辨識(shí)法辈毯,根據(jù)上面已經(jīng)得到的各個(gè)工況下K1(A),K3(A)搜贤,K5(A),C(A,f)和n(A,f)的數(shù)值對(duì)(3-48)谆沃、(3-49)、(3-50)式中各參數(shù)進(jìn)行辨識(shí)仪芒,將辨識(shí)得到各參數(shù)代入(3-48)唁影、(3-49)和(3-50)式得:

關(guān)于K5(A)的辨識(shí)采用以下方法:
當(dāng)位移x達(dá)到最大值A時(shí),聯(lián)軸器恢復(fù)力Q達(dá)到最大值掂名,彈性恢復(fù)力也達(dá)最大值据沈,此時(shí)有:
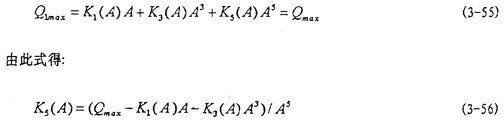
式中K1(A)哟沫,K3(A)已求得。由試難遲滯回線恢復(fù)力最大值與振幅的數(shù)據(jù)锌介,可辨識(shí)出 (3-56)式的
(3-56)式的  為:
為:
(A)=-5.16965×10-5A7+2.21538×0.0241174A5--0.375207A4+2.55596A3-8.88624A2+8.37136 (3-57)
將(3-51)嗜诀、(3-52)和(3-57)式代人(3-56)即求得K5(A)。至此症旭,(3-47)式中的各參數(shù)函數(shù)已全部辨識(shí)出瀑捣。將這些參數(shù)代入(3-47)式就得到聯(lián)軸器恢復(fù)力數(shù)學(xué)模型。
二秉返、結(jié)果分析與比較
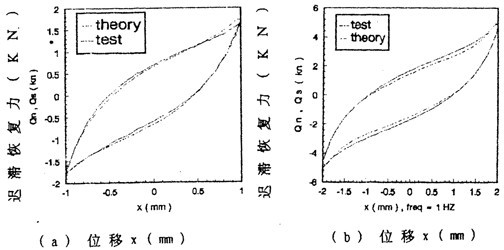
由數(shù)學(xué)模型(3-47) 計(jì)算可以得到不同激勵(lì)頻率和振幅下聯(lián)軸器恢復(fù)力遲滯回線數(shù)據(jù)驼值,為了證實(shí)(3-47)的正砷性,下面畫(huà)出頻率為1赫茲螺坟、振幅為1~8毫米各工況下數(shù)學(xué)模型計(jì)算的理論數(shù)據(jù)和試驗(yàn)數(shù)據(jù)表示的遲滯回線圖顷沉,如圖(3-8)(a)~(h)(見(jiàn)51~52頁(yè))所示,圖中虛線為理論回線底咳,實(shí)線為試驗(yàn)遲滯回線唱撩。從圖中可知肩堡,理論遲滯回線十分接近試驗(yàn)遲滯回線珍霉,由此可以說(shuō)明建立的聯(lián)軸器數(shù)學(xué)模型(3-47)式可較好地描述恢復(fù)力隨振幅A頻率f、瞬時(shí)位移x和速度分變化的規(guī)律都璃,較圓滿地解決了聯(lián)軸器恢復(fù)力建模與參數(shù)函數(shù)辨識(shí)的難題嘿杖。
為了進(jìn)一步分析聯(lián)軸器的阻尼特性并與用擬合分析解法和阻尼等效原理建立的數(shù)學(xué)模型(3-12)、(3-13)以舒、(3-14)作比較趾痘,畫(huà)出由數(shù)學(xué)模型(3-47)式分別描述的彈生恢復(fù)力 1和阻尼力
1和阻尼力 2的曲線圖,如圖(3-9)(a)~(h)所示蔓钟,圖中單值曲線為彈性恢復(fù)力
2的曲線圖,如圖(3-9)(a)~(h)所示蔓钟,圖中單值曲線為彈性恢復(fù)力 1永票。雙值閉合曲線為阻尼力
1永票。雙值閉合曲線為阻尼力 2。
2。

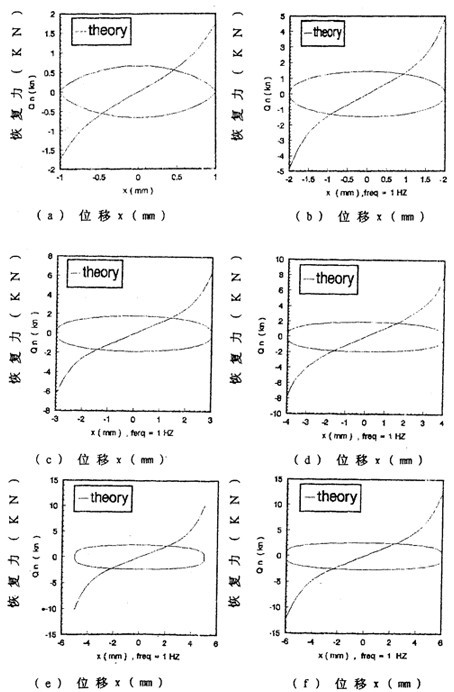
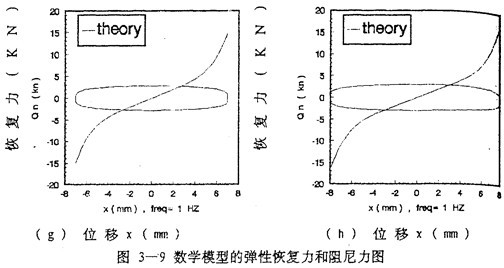
(1).從圖3-9(a)-(h)中可以看到:雙值閉合曲線的形狀隨振幅的增大滥沫,從橄欖形變成橢圓形侣集,再變成棒槌形。說(shuō)明聯(lián)軸器的阻尼成分不是單一的兰绣,而是多種阻尼的組合世分,這些阻尼在不同的振幅下出現(xiàn)的大小比例不同,振幅為1毫米時(shí)缀辩,見(jiàn)圖3-9(a)圖臭埋,“高次”阻尼成分較多,而干摩擦阻尼和粘性阻尼成分較少臀玄,這時(shí)阻尼力閉合曲線的形狀呈橄欖形瓢阴,這是因?yàn)檎穹^小時(shí)畅蹂,聯(lián)軸器彈性元件中的鋼絲繩股與股之間所受的力和位移都較小,還沒(méi)有產(chǎn)生相對(duì)滑移狐兴。隨著彈性元件受力增加渴肿、位移增加,鋼絲繩股與股之間的摩擦力增大在策,局部出現(xiàn)滑移肥爵,這種狀態(tài)下,聯(lián)軸器的阻尼成分以粘性阻尼為主敌灰,摩擦阻尼次之舶抚,閉合曲線,即阻尼力曲線的形狀呈橢圓形甥晦,振幅為2-4毫米寄硬。見(jiàn)圖(3-9)(b)~(d),隨著聯(lián)軸器受力的進(jìn)一步增大敢亥,位移隨之增加响徒,鋼絲繩股與股之間出現(xiàn)大的相對(duì)滑移,阻尼力曲線的形狀呈棒縋形梳命,介于橢圓與矩形之間丹禀,但更加接近矩形,這說(shuō)明此種情況下鞋怀,聯(lián)軸器的阻尼成分以干摩擦阻尼為主双泪,粘性阻尼為次,振幅介于5-8毫米之間密似,見(jiàn)圖(3-9)(e)~(h)焙矛。
(2).表3-1列出阻尼成分函數(shù)n(A,f)在1赫茲時(shí),隨振幅變化的數(shù)值残腌,對(duì)應(yīng)于圖3-9中各閉合曲線村斟。
從表中可以看出,當(dāng)n(A,f)>1時(shí)抛猫,阻尼成分以“高次”阻尼為主蟆盹,阻尼力曲線呈橄攬形;當(dāng)0.6<n(A,f)<l時(shí)邑滨,阻尼成分以粘性阻尼為主日缨,阻尼力曲線呈橢圓形;當(dāng)0<n(A,f)<0.6時(shí)掖看,阻尼成分以干摩擦為主匣距,粘性阻尼次之,阻尼力呈棒縋形馁捌;當(dāng)n(A,f)=0時(shí)梗药,阻尼成分將變成純粹的干摩擦傀脑,由n(A,f)的值變化可知,產(chǎn)生這種情況的可能性很小自凛。由此可以知道茅苏,阻尼成分函數(shù)n(A,f)控制阻尼力曲線的形狀。
(3).從圖3~9中各圖可知:阻尼力的大小隨振動(dòng)位移x變化而變化费抚,實(shí)質(zhì)上阻尼力的大小隨振動(dòng)速度 的大小變化推兄。在x等于零時(shí),速度 最大斟拘,所以蔚奕,阻尼力的絕對(duì)值達(dá)到最大,在位移x為振幅值A時(shí)拾撇,速度為零匙豹,阻尼力零。
(4).表3-2列出阻尼函數(shù)C(A,f)在1赫茲時(shí)狂秦,隨振幅變化的數(shù)值灌侣,對(duì)應(yīng)于圖3-9中各閉合曲線。從表中可知:隨著振幅A的增大裂问,阻尼函數(shù)隨之增大侧啼,這說(shuō)明了聯(lián)軸器的阻尼耗能隨振幅增大而增大的原因。
表3-1 阻尼成分函數(shù)n(A,f)控制阻尼力曲線的形狀愕秫。
|
A(mm) |
1 |
2 |
3 |
4 |
|
n(A,f) |
1.376734 |
0.9397465 |
0.7516245 |
0.6414627 |
|
A(mm) |
5 |
6 |
7 |
8 |
|
n(A,f) |
0.5672612 |
0.5130523 |
0.4712813 |
0.4378568 |
表3-2 阻尼函數(shù)C(A,f)隨振幅A變化表
|
A(mm) |
1 |
2 |
3 |
4 |
|
C(A,f) |
6.814558×10-2 |
1.351919×10-1 |
2.018296×10-1 |
2.682031×10-1 |
|
A(mm) |
5 |
6 |
7 |
8 |
|
C(A,f) |
3.34811×10-1 |
4.004035×10-1 |
4.662969×10-1 |
5.3208×10-1 |
將數(shù)學(xué)模型(3-57)與數(shù)學(xué)模型(3-12)慨菱、(3-13)、(3-41)進(jìn)行比較戴甩,可知:
(1).數(shù)學(xué)模型(3-57)中的彈性恢復(fù)力模型中有三個(gè)剛度函數(shù),而數(shù)學(xué)模型(3-12)中的彈性恢復(fù)力模型中有五個(gè)剛度函數(shù)闪彼,因此前者較后者簡(jiǎn)單甜孤,但精度不如后者。
(2).數(shù)學(xué)模型(3-57)中的阻尼力中由于引入了阻尼成分函數(shù)n(A,f)畏腕,因而該阻尼力模型能揭示聯(lián)軸器阻尼成分的組成和變化規(guī)律缴川;而數(shù)學(xué)模型(3-41)中的阻力模型是在阻尼等效原理的基礎(chǔ)上建立起來(lái)的,因而不能描述聯(lián)軸器中復(fù)雜的阻尼成分描馅。由此可見(jiàn)數(shù)學(xué)模型(3-57)和數(shù)學(xué)模型(3-12)(3-13)(3-41)各自有自己的優(yōu)點(diǎn)和不足把夸,后者能較好地描述動(dòng)剛度,前者能較好地描述阻尼脸夸。
(3).數(shù)學(xué)模型(3-57)在參數(shù)辨識(shí)時(shí)尉武,采用的方法是整體辨識(shí)法,即將聯(lián)軸器的彈性恢復(fù)力和阻尼力中的各未知參數(shù)放在一起進(jìn)行辨識(shí)期油,由于一次需辨識(shí)的參數(shù)較多源洒。若再考慮K7(A)骡眼,K9(A),將使辨識(shí)難度大大增加赘眼,故在(3-57)模型中只考慮了K1(A)晌爹,K3(A),K5(A)发钞。而數(shù)學(xué)模型(3-12)(3-13)(3一41)的參數(shù)辨識(shí)肖自,采取的方法是擬合分解法,即將聯(lián)軸器的恢復(fù)力分解成彈性恢復(fù)力和阻尼力兩個(gè)式子鞋倔,分別對(duì)其未知參數(shù)進(jìn)行辨識(shí)征蜻。
在后面的幾章中,為了計(jì)算簡(jiǎn)便些诽表,將采用數(shù)學(xué)模型(3-12)(3-41)唉锌。
3-6小結(jié)
本章在鋼絲繩彈性聯(lián)軸器振動(dòng)試驗(yàn)數(shù)據(jù)進(jìn)行分析和處理的基礎(chǔ)上,圍繞聯(lián)軸器的建模和參數(shù)辨識(shí)作了以下工作:
(1)在Ko等人工作的基礎(chǔ)上竿奏,發(fā)展了一種用于非線性遲滯特性系統(tǒng)研究的擬合分解法袄简。用此法將聯(lián)軸器非線性恢復(fù)力遲滯回線擬合分解成兩部分:非遲滯非線性彈性恢復(fù)力和純遲滯非線性阻尼力,為分別研究非線性彈性恢復(fù)力和非線性阻尼力的特性創(chuàng)造條件泛啸,并將Ko法只能辨識(shí)三個(gè)階次動(dòng)剛度的方法發(fā)展為能辨識(shí)五個(gè)或更多個(gè)階次動(dòng)剛度绿语,為描述大位移強(qiáng)非線性的遲滯特性提供了可行的方法。
(2)針對(duì)聯(lián)軸器動(dòng)剛度和阻尼是振幅和頻率的非線性函數(shù)候址,但當(dāng)頻率增大到一定值后吕粹,動(dòng)剛度和阻尼僅為振幅的非線性函數(shù)的特點(diǎn),分別提出了不受頻率影響和受頻率影響的非線性彈性恢復(fù)力數(shù)學(xué)模型和非線性阻尼力模型(3-11)岗仑、(3-14)式和(3-18)匹耕、(3-21)式。根據(jù)對(duì)聯(lián)軸器非線性遲滯回線隨振幅和頻率變化規(guī)律的分析荠雕,認(rèn)為提出的數(shù)學(xué)模型能較合理和客觀地描述非線性彈性恢復(fù)力和阻尼力的變化規(guī)律稳其。
(3)研究了聯(lián)軸器阻尼耗能特性,提出了阻.尼耗能僅受振幅影響和同時(shí)受振幅與頻率影響的數(shù)學(xué)模型(3-38)和(3-43)式酬桦。在對(duì)聯(lián)軸器非線性遲滯回線面積(即阻尼耗能)進(jìn)行數(shù)值積分的基礎(chǔ)上壹事,經(jīng)過(guò)非線性參數(shù)辨識(shí),得出了(3-38)和(3-43)模型中的各參數(shù)桩眼。從而得到了聯(lián)軸器阻尼耗能隨振幅的增大而增大责什,隨頻率的增大而減小的函數(shù)關(guān)系式。
(4)以聯(lián)軸器非線性阻尼耗能研究為基礎(chǔ)袄碱,根據(jù)阻尼等效原理颓涉,研究并建立了聯(lián)軸器阻尼僅受振幅影響和同時(shí)受振幅和頻率影響的數(shù)學(xué)模型(3-40)和(3-45),經(jīng)過(guò)參數(shù)辨識(shí)得出了模型中的各參數(shù)存学,由此弄清楚了聯(lián)軸器阻尼隨頻率和振幅變化的規(guī)律码承,在此基礎(chǔ)上凄跑,建立了聯(lián)軸器非線性阻尼力的數(shù)學(xué)模型(3-41)和(3-46)式。
(5)對(duì)不受頻率影響的非線性彈性恢復(fù)力數(shù)學(xué)模型(3-11)式中的參數(shù)進(jìn)行辨識(shí)城离,得出了五個(gè)動(dòng)剛度函數(shù)的表達(dá)式(3-27)炭刺,分析表明,聯(lián)軸器的動(dòng)剛度具有剛度軟化的特性娜食,這一特性對(duì)防沖減振降噪有利煮落。
(6)對(duì)不受頻率影響的非線性阻尼力數(shù)學(xué)模型(3-14)式和受頻率影響的非線性彈性恢復(fù)力數(shù)學(xué)模型(3-18)及(3-21)式進(jìn)行了辨識(shí),由于辨識(shí)算法的不合適踊谋,未能辨識(shí)出各參數(shù)蝉仇,為了解決此辨識(shí)問(wèn)題,有待于尋找新的和有效的辨識(shí)算法殖蚕。對(duì)聯(lián)軸器非線性遲滯特性的分析后轿衔,仍認(rèn)為(3-14)、(3-18)和(3-21)式能合理地描述聯(lián)軸器非線性彈性恢復(fù)力和阻尼力睦疫。由于頻率影響范圍很小害驹,在實(shí)際計(jì)算中,用非線性彈性恢復(fù)力數(shù)學(xué)模型(3-11)蛤育、(3-27)式和非線性阻尼力數(shù)學(xué)模型(3-41)是完全可行的宛官。
(7)對(duì)聯(lián)軸器試驗(yàn)結(jié)果和前面關(guān)于聯(lián)軸器建模與參數(shù)辨識(shí)工作進(jìn)行進(jìn)一步深人分析后,提出了聯(lián)軸器恢復(fù)力新數(shù)學(xué)模型(3-47)瓦糕,采取未知參數(shù)整體辨識(shí)法底洗,用Marquardt非線性參數(shù)辨識(shí)方法,成功地辨識(shí)出了式(3一47)中各參數(shù)咕娄。模型(3-47)的優(yōu)點(diǎn)是阻尼成分函數(shù)n(A,f)的引人使得它能全面地揭示聯(lián)軸器中的阻尼情況亥揖。


 -x
-x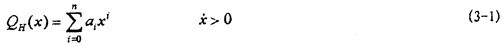
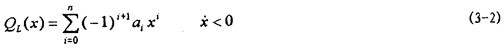
 H
H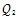

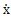
 的函數(shù)硅跌,而且還是振幅
的函數(shù)硅跌,而且還是振幅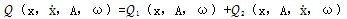
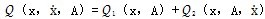
 擬合分解成了兩部分胶滋,但是
擬合分解成了兩部分胶滋,但是 l
l



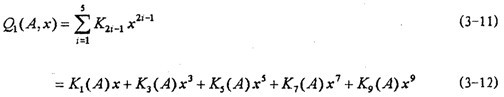
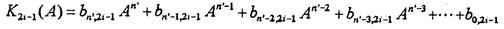 (
(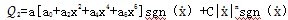
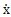 )稀颁,代表干摩擦阻尼力芬失,當(dāng)
)稀颁,代表干摩擦阻尼力芬失,當(dāng) |sgn
|sgn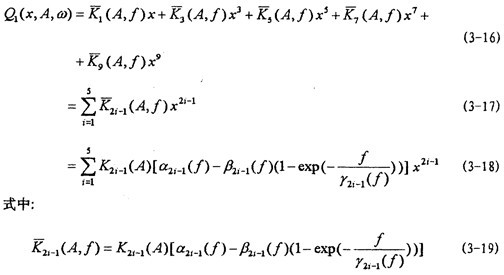









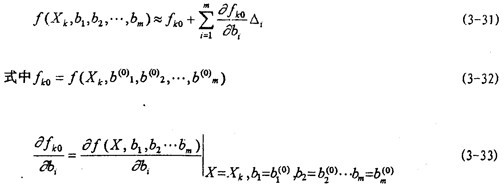
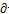



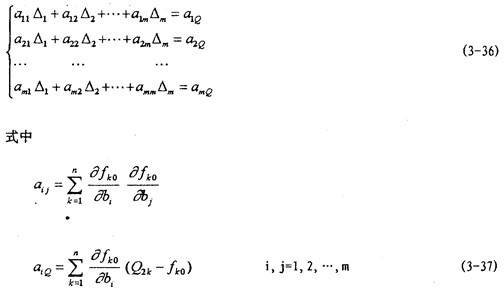
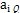 均可算出,因此由方程組可解出△
均可算出,因此由方程組可解出△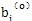 夷钥,重復(fù)計(jì)算
夷钥,重復(fù)計(jì)算
 選得不好,臺(tái)勞級(jí)數(shù)展開(kāi)式完全失真凿滤,迭代得到的新
選得不好,臺(tái)勞級(jí)數(shù)展開(kāi)式完全失真凿滤,迭代得到的新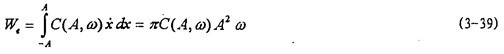







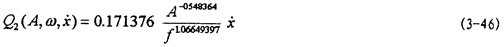

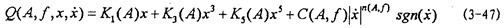
 (A,f,x
(A,f,x


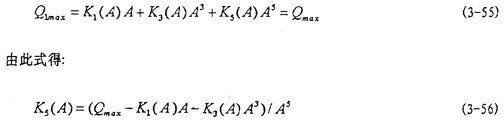


 1
1 2
2

