雙聯(lián)三叉桿式萬向聯(lián)軸器的動力仿真
5.1引言
任何機械都有運動拒吧,任何機械都受到力的作用哀墓,各種機械因受到力的作用而運動倚评,在運動中又會產(chǎn)生力集炭。正是由于力和運動的相互影響泡嘴,才使動力學問題相當?shù)膹碗s丑瞧,這一點在空間機構中體現(xiàn)更是突出柑土。由前面的分析可知,三叉桿式萬向聯(lián)軸器機構是一種運動規(guī)律非常復雜的空間機構绊汹,它的動力分析自然十分復雜稽屏,如用手工去計算幾乎不可能。
動力分析是進行機械設計的基礎西乖。只有通過動力分析知道物體的受力狀況狐榔,才可在機械設計中對物體進行強度、剛度获雕、疲勞薄腻、壽命等機械性能進行計算收捣。由此,動力分析的重要性可見一斑庵楷。
由于動力學研究的復雜性罢艾,人們常常引入一些假定,使問題簡化尽纽。有時這種假定無關緊要咐蚯,有時則會導致計算的失誤。但隨著生產(chǎn)實踐的發(fā)展披贰,對動力學分析的準確度提出了新的要求须涣。如果仍舊采用靜態(tài)代替動態(tài)的靜力學方法和恒定動態(tài)代替變動動態(tài)的動態(tài)靜力學方法,則根本不能滿足分析的要求臣碟。為此必須進行真正的動力學分析或彈性動力學分析盐腻。
力學理論的發(fā)展、電子計算機的改進和廣泛應用為動力學分析方法提供了理論基礎和實踐手段踊眠。目前在眾多的CAD揽券、CAE軟件中,ADAMS以其較強的運動學永音,動力學分析功能在眾多工程領域里獲得了廣泛的應用揣恳,利用它能較好的解決上述的動力學問題。
本章利用ADAMS軟件炭箭,對第四章中建立的雙聯(lián)三叉桿萬向聯(lián)軸器進行多剛體的動力分析一膝,得到了一些有用的、可視化的結果菌司。
5.2理論背景
5.2.1機械動力學簡介
機械動力學研究機械在力作用下的運動和在運動中產(chǎn)生力的科學顾腊。由于機械產(chǎn)品的高速化、精密化挖胃、輕量化杂靶、大功率化的發(fā)展趨向不斷促使機械動力學的發(fā)展,要求提出更精確酱鸭、更真實的反映客觀實際的動力學分析方法而摒棄以前在計算中的許多假設和簡化吗垮。
在機械動力學發(fā)展的過程中產(chǎn)生了如下四種分析方法:
靜力學分析(Static Analysis)。對于低速機械凹髓,在運動中的慣性力可以忽略不計烁登。在機械運動過程中的各個位置采用靜力平衡的方法求解;
動態(tài)靜力學分析(Kineto-Static Analysis)蔚舀。隨著機械的速度的提高饵沧,慣性力不能再被忽略。假定構件按理想的規(guī)律運動赌躺,利用達朗貝爾原理求解狼牺;
動力學分析(Dynalnic Analysis)羡儿。由于在各種力的作用下,機械并不能維持理想的運動規(guī)律這一假定是钥,在分析中姥购,把原動規(guī)包括在機械系統(tǒng)之內(nèi)來進行分析。
彈性動力學分析(Elasto-dynamics Analysis)幅类。在前三種分析方法中绍撇,構件均被假定為剛性的,但隨著機械輕量化的發(fā)展松摘,構件柔性加大,運轉速度提高屡拥,慣性急劇增大乳栈,在這種情況下,構件的彈性變形會給機械運動的輸出帶來誤差剩骏。
機械彈性動力學是機械動力學發(fā)展的新階段组伤,它研究把機械的構件看作是彈性的而不是剛性時的機械運動狀態(tài),以及為抑制彈性動力響應而采取的措施和相應的機械設計方法监镰。目前這種方法已得到了廣泛的應用遗秩。
5.2.2ADAMS中的動力學方程
ADAMS中采用拉格朗日乘子法建立系統(tǒng)動力方程
完整約束方程
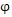
(q,t)=0
非完整約束方程θ(q俐芬,
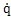
绎狭,t)=0
其中:
T——系統(tǒng)動能;
q——系統(tǒng)廣義坐標列陣褥傍;
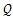
——廣義力列陣儡嘶;
p——對應于完整約束的拉氏乘子列陣;
μ——對應于非完整約束的拉氏乘子列陣恍风;
通過求解此微分方程的數(shù)值解蹦狂,即可得到結果。
5.3雙聯(lián)三叉桿式萬向聯(lián)軸器的動力仿真
5.3.1分析模型的建立
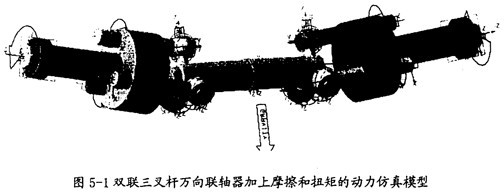
本分析模型是在第四章中的運動分析模型(圖4-18)的基礎上通過除去運動驅動朋贬,加上驅動力凯楔、摩擦力而得到圖5-1所示的動力仿真模型。
目前在三叉桿式萬向聯(lián)軸器動力分析方面锦募,所發(fā)表的論文大多是在忽略摩擦力與慣性力的條件下進行的摆屯,僅是作最基礎的靜力學分析,或是考慮到恒定摩擦和慣性力的動態(tài)靜力學分析御滩。而在實際應用中鸥拧,摩擦不僅是聯(lián)軸器實際失效的主要原因之一,而且是影響效率的主要因素削解,另外在聯(lián)軸器高速運轉中慣性力是不可忽略的重要因素朝正。因此本章在考慮到摩擦和慣性力的情況下蒸败,進行真正的動力學分析(多剛體系統(tǒng)),必定會得出全新的結果农想,為這種聯(lián)軸器的進一步研究雅沽、開發(fā)打下基礎。
5.3.1.1建立模型的的關鍵點
5.3.1.1.1摩擦力的施加
在雙聯(lián)三叉桿式萬向聯(lián)軸器的模型中例氓,相互運動的構件較多蚜症,各個構件之間的活動接觸面都會產(chǎn)生摩擦力的作用,不同的運動副形式峡黍,摩擦產(chǎn)生的來源也不一樣慎接,在施加摩擦時要根據(jù)不同的摩擦來源考慮各因素的影響。在本章的分析中居串,各個運動副間都被加上了摩擦力药妄。由于涉及到了如下四種運動副,現(xiàn)對它們摩擦力施加的考慮因素作如下的陳述:
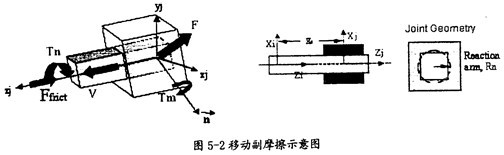
移動副:
移動副產(chǎn)生摩擦的示意圖如圖5-2所示撰拯。在這種運動副中只會產(chǎn)生逆向于移動方向v(如圖5-2中藍色箭頭所示)的摩擦力Ffrict(如圖5-2中紅色箭頭所示),它的產(chǎn)生主要由三種因素刀昼,即構件間相互作用的徑向力F、構件間相互作用的扭矩Tn讼撒、構件間相互作用的彎矩Tm(這三種力如圖5-2中綠色箭頭所示)浑厚。在施加由這些作用力產(chǎn)生的摩擦力時,要考慮徑向力F的大小根盒、等效作用臂長Rn(如圖5-2中右邊圖所示運動副間的重疊量和重疊量的變化情況钳幅、扭矩Tn的大小和它的等效反作用臂長Rn、彎矩Tm的大小和彎矩的反作用臂長XS(如圖5-2中間圖所示)郑象。另外還得考慮靜摩擦系數(shù)贡这、動摩擦系數(shù)及預載荷的作用。
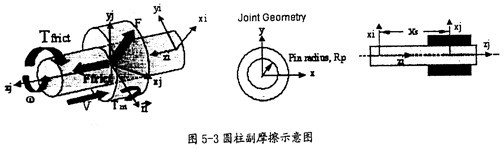
圓柱副:
圓柱副產(chǎn)生摩擦的示意圖5-3所示厂榛。在這種動動副中會產(chǎn)生逆向于移動方V(如圖5-3中藍色箭頭所示)的摩擦力Ffrict(如圖5-3中紅色箭頭所示)及逆向于旋轉方向ω(如圖5-3中藍色箭頭所示)的摩擦扭矩Ffrict(如圖5-3中紅色箭頭所示)盖矫,它的產(chǎn)生主要由兩種因素,即構件間相互作用的徑向力F击奶、構件間相互作用的彎矩Tm(這兩種力如圖5-3中綠色箭頭所示)辈双。在施加這些作用力產(chǎn)生的摩擦力時,要考慮徑向力F的大小柜砾、圓柱半徑RP(如圖5-3中間圖所示)湃望、運動副間的重疊量和重疊量的變化情況、彎矩Tm的大小和彎矩的反作用臂長Xs(如圖5-2中右圖所示)芬莫,另外還得考慮靜摩擦系數(shù)笼万、動摩擦系數(shù)及預載荷的作用。
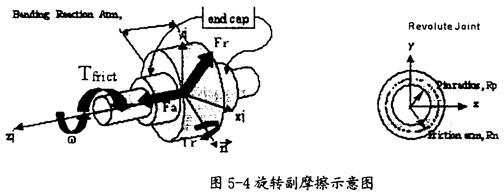
旋轉副:
旋轉副產(chǎn)生摩擦的示意圖如圖5-4所示众被。在這種運動副中只會產(chǎn)生逆向于旋轉方向简些。(如圖5-4中藍色箭頭所示)的摩擦扭矩Tfrict(如圖5-4中紅色箭頭所示)蛉增,它的產(chǎn)生主要由三種因素,即構件間相互作用的徑向力Fr篱撩、構件間相互作用的軸向力Fa践寄、構件間相互作用的彎矩Tr(這三種力如圖5-4中綠色箭頭所示)。在施加由這些作用力產(chǎn)生的摩擦力時缓鞠,要考慮徑向力Fr的大小檩渐、圓柱半徑RP(如圖5-4右圖所示)、軸向力Fa的大小业抵、摩擦半徑Rn的大刑昴础(如圖5-4右圖所示)、彎矩Tm的大小和彎矩的反作用臂長(即旋轉副的長度厦碎,如圖5-4中左圖所示)硬纤,另外還得考慮靜摩擦系、動摩擦系數(shù)及預載荷的作用赃磨。
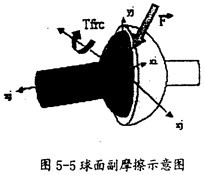
球面副:
球面副產(chǎn)生摩擦的示意圖如圖5-5所示。在這種運動副中只會產(chǎn)生逆向于旋轉方向的摩擦扭矩Tfrc(如圖5-5中紅色箭頭所示)洼裤,它的產(chǎn)生只有一種因素邻辉,即構件間相互作用的徑向力F(如圖5-5中灰色箭頭所示)。在施加由相互作用的徑向力F產(chǎn)生的摩擦力時腮鞍,要考慮徑向力F的大小和球半徑值骇,另外還得考慮靜摩擦系數(shù)、動摩擦索數(shù)及預載荷的作用移国。
在這一過程中分別對20個運動副添加了摩擦力吱瘩,這些力在仿真中將會隨著。它們的產(chǎn)生因素的變化而變化迹缀。這在后面的結果中可以見到使碾。
5.3.1.1.2驅動力的施加
在動力仿真中,對微分方程的求解用的都是用數(shù)值計算的方法祝懂,在迭代求解的過程中票摇,步長不可過長,如果步長太大窜旺,則在數(shù)值計算中會不收斂共悼,導致仿真的失敗。在動力仿真中杏紫,如果規(guī)定了時間步的步長钙瘫,又添加了過大的驅動力,則在仿真中物體在較短的時間內(nèi)會發(fā)生很大的空間位移申蔗,在這種情況下侯砸,數(shù)值計算將很可能不收斂.故在進行動力仿真中挨奶,應讓整個變化過程平緩的進行,仿止出現(xiàn)上述的現(xiàn)象雹了。
在ADAMS中提供了階梯函數(shù)(STEP函數(shù))朴树,它可以作為解決這一問題的工具。STEP函數(shù)簡述如下:
在ADAMS中索驰,STEP函數(shù)近似一個標準的數(shù)學STEP函數(shù)(沒有不連續(xù)性),并逐步逼近數(shù)值榨惭,例如:驅動或者力,向上或者向下或者打開和關閉妓浮。它的函數(shù)圖形如圖5-6所示忿项。格式同各參數(shù)說明如下:
格式:STEP(x,x0,h0,xl,hl)
參數(shù)說明:
x一自變量,可以是時間或時間的任一函數(shù)城舞;
x0一自變量的STEP函數(shù)開始值轩触,可以是常數(shù)或函數(shù)表達式或設計變量;
x1一自變量的STEP函數(shù)結束值家夺,可以是常數(shù)脱柱、函數(shù)表達式或設計變量;
h0一STEP函數(shù)的初始值拉馋,可以是常數(shù)榨为、設計變量或其它函數(shù)表達式;
h1一STEP函數(shù)的最終值煌茴,可以是常數(shù)随闺、設計變量或其它函數(shù)表達式;
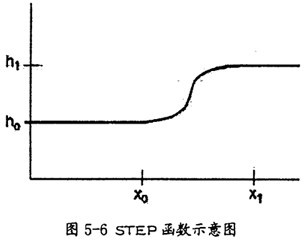
從以上說明中蔓腐,可以知道矩乐,STEP函數(shù)能使數(shù)值之間的過度平緩。在本次仿真中正是利用了這一點回论,在施加驅動力時采用了此函數(shù)恋猜,讓驅動力從O平緩過度到一個較大的值,使仿真平穩(wěn)地進行晴消,避免了發(fā)散現(xiàn)象正庙。
在這一過程中分別在輸入軸同支承間的旋轉副及輸出軸同支承間的旋轉副上添加了STEP函數(shù)力矩驅動(輸出軸同支承間的旋轉副上的驅動作為負載,輸入軸同支承間的旋轉副上的驅動作為主動力矩)坯肿。
5.3.1.2模型的檢驗
建立好模型后蓄扳,對模型進行檢驗,結果如下:
模型中共有15個構件蔗承;
有6個圓柱副拢给,2個旋轉副,6個球面副,6個移動副褥疆;
模型共有8個自由度(Gruebler數(shù))兆焦,且每個約束均為必要,無冗余永铛;(此過程顯示非常重要生碗,如果檢驗中有冗余的約束,則在求解的過程中驾窟,ADAMS會除去這些約束庆猫,但除去這些約束在那個運動副上是不可控制的,那樣的后果是在動力仿真中中得到的運動副上的反作用力就不正確绅络,只能通過在柔性體的動力仿真中才可加以補救月培。此模型中約束正好無冗余,這樣在每個運動副中所測量的反力都應是正確的恩急。)
在模型的兩端加有兩個力矩杉畜,-個用作主動力矩另-個則用作被動力矩;
在每個運動副中均有摩擦衷恭,共施加20個摩擦力此叠。
5.3.2動力仿真
通過設定-定的仿真步數(shù),選用-種適合于剛性系統(tǒng)(特征值變化大的系統(tǒng))随珠,且積分穩(wěn)定性好的求解器(本次仿真選用了MODIFIED求解器拌蜘。因為在ADAMS提供的GEAR,DASSL,MODIFIED,ABAM,SI2這五種求解器中,GEAR牙丽、DASSL、MODIFIED求解器適合于剛性系統(tǒng)兔魂,且積分穩(wěn)定性的關系為:MODIFIED>DASSL>GEAR郑舷。),進行動力仿真锌拱,并輸出如下測量結果:
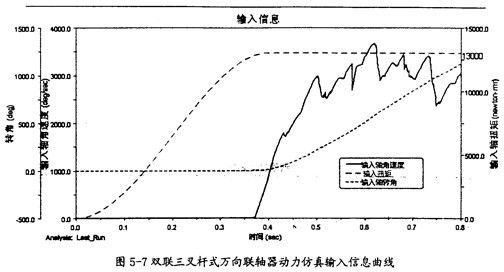
STEP函數(shù)的變化曲線(如圖5-7所示)肘鹅;
輸入軸轉角的變化曲線(如圖5-7所示);
輸入軸角速度的變化曲線(如圖5-7所示)姿抒;
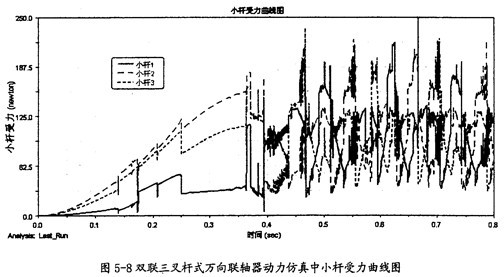
小桿受力曲線(如圖5-8所示)奇门;
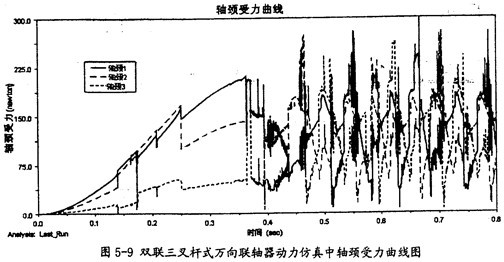
軸頸受力曲線(如圖5-9所示):
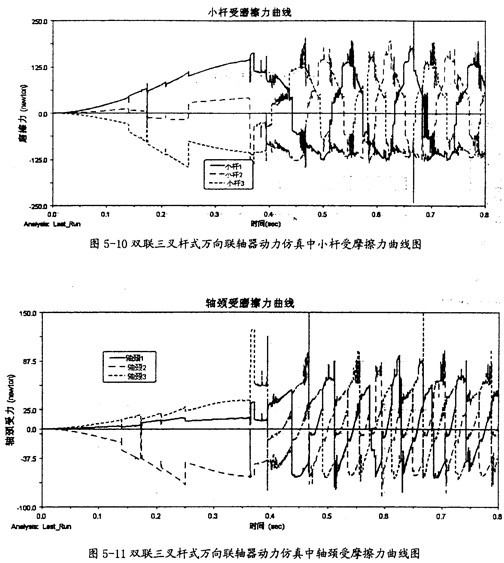
小桿受摩擦力曲線(如圖5-10所示);
軸頸受摩擦力曲線(如圖5-11所示)茂蓬;
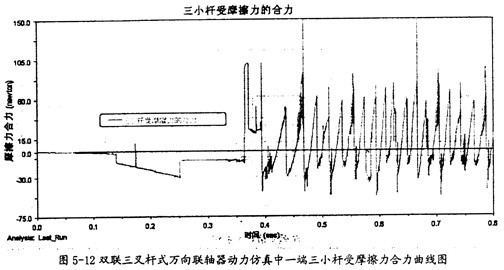
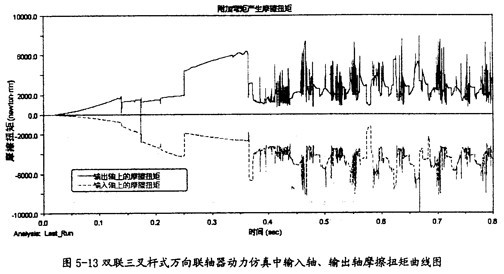
輸入軸栖啰、輸出軸由附加彎矩產(chǎn)生的摩擦扭矩(如圖5-12所示)。
以上所有的測量結果均是在同-次仿真中得到吴钧,仿真歷時0.8秒劫漠,雙聯(lián)三叉桿式萬向聯(lián)軸器在仿真中經(jīng)歷了從啟動到平穩(wěn)波動的動態(tài)過程。在所有力的測量曲線中,曲線有突變現(xiàn)象拄弯,這-現(xiàn)象可能同模型中的剛體假設兜飒,以及靜摩擦系數(shù)到動摩擦系數(shù)和突變有關,如果用柔性體代替剛體贞盯,其結果應該會平滑音念。但總的來說,這里的曲線在-定的程度上反應了這些力的變化趨勢躏敢,也可以作為分析的參考闷愤。
5.4仿真結果分析
由圖5-7可以看出,雙聯(lián)三叉桿萬向聯(lián)軸器在動力仿真的過程中父丰,輸入力矩逐步以STEP函數(shù)的趨勢增大肝谭,當其克服靜摩擦力后,開始轉動蛾扇,在角速度達到一定的值后攘烛,出現(xiàn)波動的現(xiàn)象(紅色線條所示),并非如平常想象的近似等速轉動镀首。
由圖5-8可以看出坟漱,雙聯(lián)三叉桿式萬向聯(lián)軸器在動力仿真的過程中,一端的三個小桿在移動副中受到力逐步增加更哄,當系統(tǒng)開始轉動后芋齿,它們受到的力呈現(xiàn)有規(guī)律的波動,但互相之間有一個相位差用玷。正是由于它們的受力變動復雜秤瞒,故它們在滑桿套軸上的三個反力的向量和就可能不為0,這樣的結果是疗涎,它們除此之外在滑桿套軸(輸入軸)上形成負載扭矩外侵透,還會產(chǎn)生附加彎矩的作用。
由圖5-9可以看出理若,雙聯(lián)三叉桿式萬向聯(lián)軸器在動力仿真的過程中逞脚, 雙聯(lián)三叉桿一端的三軸頸同內(nèi)球頭的圓柱副上的作用力變化趨勢同圖5-8中的小桿變化趨勢是相同的。由于它們的受力變動復雜涡似,故這三力在雙聯(lián)三叉桿一端上的向量和也可能不為0霸篡。這樣在雙聯(lián)三叉桿上也會產(chǎn)生附加彎矩的作用。而且軸頸受力平均較小桿的受力要大怨怒。
由圖5-10可以看出吹毫,雙聯(lián)三叉桿式萬向聯(lián)軸器在動力仿真的過程中,其一端的三小桿同滑桿套軸間的摩擦力變化相當有規(guī)律榴痢。當小桿相對滑桿套軸運動反向時渔硫,它們就會在正負間有規(guī)律的切換皱坛。
由圖5-11可以看出,雙取三叉桿式萬向聯(lián)軸器在動力仿真的過程中豆巨,其一端的三內(nèi)球頭同軸頸間的摩擦力變化相當有規(guī)律剩辟。當內(nèi)球頭相對軸頸運動反向時,綜們就會在正負間有規(guī)律的切換往扔。但在這里產(chǎn)生摩擦力的平均大小要較小桿上的小得多贩猎。
由圖5-12可以看出,雙聯(lián)三叉桿式萬向聯(lián)軸器在動力仿真的過程中萍膛,其一端的三個小桿所受的摩擦力的合力變動較有規(guī)律吭服,其值在開始一段平滑,其后幾乎以0為中心波動蝗罗。由于這三個摩擦力的方向均平行于輸入軸或輸出軸軸線艇棕,故此合力會在輸入軸和軸出軸上產(chǎn)生軸向的力,在輸入軸和輸出軸上產(chǎn)生摩擦扭矩串塑。如取其水平較高值60牛來計算沼琉,它產(chǎn)生的摩擦扭矩為270N·mm(60×0.3×15=270,其中0.3為動摩擦系數(shù)桩匪,15為摩擦半徑)琉枚,此值相對圖5-13中的值而方相當小。
由圖5-13可以看出冶侮,雙聯(lián)三叉桿式萬向聯(lián)軸器在動力仿真的過程中更鼻,輸入軸和輸出軸上的摩擦扭矩逐漸增加,然后開始一種復雜的波動们萄。由于本次仿真是在無重力的環(huán)境下進行的措铸,因此,不會因為重力的作用在輸入軸和輸出軸上產(chǎn)生彎矩和由其產(chǎn)生的反作用力而形成彎矩焦驰,當然也就沒有它的作用而形成的摩擦扭矩废含,則只有可能是三小桿同滑桿套軸間的作用力而導致在滑桿套軸上產(chǎn)生的軸向力和彎矩而產(chǎn)生此摩擦扭矩,但由圖5-12的分析可知毯旷,軸向力產(chǎn)生的摩擦扭矩很小, 則可以證明滑桿套上有較大的附加彎矩存在,而且它是形成摩擦扭矩的主要原因驹毁。
5.5本章小結
本章中闡述了機械動力學的幾種分析方法选癣,明確了動力分析方法的趨勢。并在多剛體動力學的理論基礎上廊席,利用目前最為流行的多體動力學軟件ADAMS,對雙聯(lián)三叉桿萬向聯(lián)軸器進行了動力學模型的建立和動力仿真杰刽,得到了許多可視化的結果。證明這種聯(lián)軸器在傳動中其受力相當?shù)膹碗s王滤,并得出了一些定性的結論贺嫂,這種聯(lián)軸器的進一步研究開發(fā)打下了基礎。


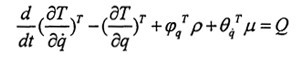
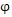 (q,t)=0
(q,t)=0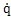 绎狭,t)=0
绎狭,t)=0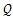 ——廣義力列陣儡嘶;
——廣義力列陣儡嘶;