三叉桿式萬向聯(lián)軸器的理論運動分析
3.1前言
三叉桿式萬向聯(lián)軸器是一種新型的萬向聯(lián)軸器,它在結構上簡單紊尺、緊湊彰晌、安裝方便,具有承載能力大和工作可靠等優(yōu)點达吞。在國外已廣泛地被應用于汽車工業(yè)和其它的工業(yè)領域张弛。但由于它的運動規(guī)律復雜,為了徹底弄清它的特點酪劫,長期以來一直都有人對它運用不同的計算方法進行運動分析吞鸭。本章運用方向余弦矩陣這一數(shù)學工具,對三叉桿滑移式萬向聯(lián)軸器運動機理進行解析計算覆糟,得出它的運動規(guī)律表達式和曲線圖刻剥,并在后面的章節(jié)中運用同樣的結構進行仿真驗證,以檢驗計算的正確性滩字。
3.2三叉桿式萬向聯(lián)軸器的理論運動分析
3.2.1三叉桿滑移式萬向聯(lián)軸器簡介
三叉桿滑移式萬向聯(lián)軸器由滑桿套軸(又稱為輸入軸)造虏、三叉桿(又稱為輸出軸)、小桿和內球頭等組成產(這幾個構件的模型圖3-1所示)麦箍,其中小桿和內球頭裝配成滑桿(模型的裝配關系如圖3-l最上部)漓藕,在這種連接形式下陶珠,內球頭可在小桿內轉動,即形成球面副享钞,具有三個轉動自由度揍诽。在滑桿套軸上有三個均勻分布的孔(小桿的滑道),與安裝在三叉桿軸頸上的滑桿相配合泄楷,這里所有的配合均為間隙配合竖枚。當三叉桿萬向聯(lián)軸器運轉時(兩軸有夾角),滑桿一方面沿滑道的中心線移動眠荒,另一方面沿三叉桿軸頸移動路棍,從而實現(xiàn)運動過程中的角度補償。
3.2.2分析模型的建立
由于運動規(guī)律的特殊性意苞,為了實現(xiàn)它的運動祖匕,對單聯(lián)的三叉桿式萬向聯(lián)軸器需要在輸出軸上安裝調心軸承(調心軸承的模型裝配關系如圖3-1所示,它的內圈同三叉桿無相對滑動)美域,否則它在理論上是不可以轉動的(自由度不夠)汪怒。再裝上機架,即左支承(如圖3-1)茧纵,就構成了三叉桿滑移式萬向聯(lián)軸器的裝配模型杭厘。其模型如圖3-2所示。
通過對圖3-2中的模型進行抽象郭销,可得到三叉桿滑移式萬向聯(lián)軸器的機構運動簡圖隶丁,其示意圖如圖3-3所示,在此模型中關節(jié)軸承中心同三叉桿三軸頸軸線的交點距離一直不變呕童。由以前的分析可知漆际,在這種模型中,三叉桿中心的運動軌跡在輸出軸平行于自身運動時是以
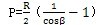
為半徑的圓夺饲,其中R為輸入軸滑道軸線至奸汇。輸入軸軸線的距離(圖3-4中有其示意),β為輸入往声、輸出兩軸線之間的夾角(圖3-5中有其示意),L為圓錐擺中軸線長擂找。所以采用調心軸承安裝輸出軸時,輸出軸的運動必為一圓錐擺運動浩销,三叉桿中心的偏心距P比值

有關贯涎。當L為無窮大時,

,這時相當于用雙向心軸承安裝輸出軸慢洋,隨著

增大L
P的計算值與實際值將會出現(xiàn)微小的誤差塘雳;由于誤差極小,所以在一般應用場合可以取P≈
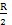
(
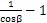
)
由于在轉動的過程中普筹,三叉桿交點作旋轉運動粉捻,因此會導致輸入軸與輸出軸之間的夾角發(fā)生變化缅含,其變化范圍為βmin~βmax,當O點(見圖3-5)處于輸入軸與輸出軸轉動錐中心線所構成平面的兩個極限位置時杖荤,偏轉角達到兩極值:
在其它位置時,偏轉角介于兩者之間篇张。
3.2.3坐標系的建立
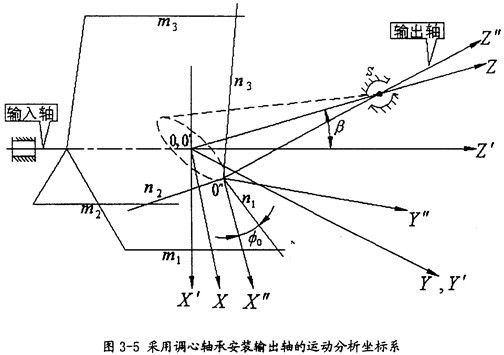
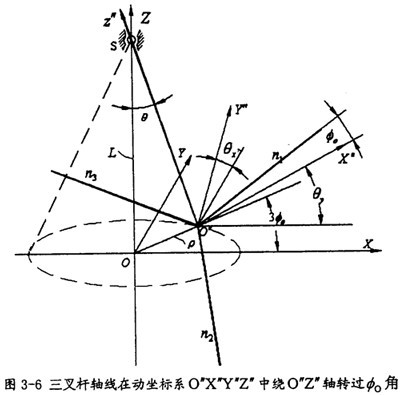
由于輸出軸作一圓錐運動窥吮,在分析的過程中需建立三套坐標系,如圖3-5所示胀蹭。
首先建立兩個固定坐標系OXYZ和O′X′Y′Z′哗搏,輸出軸轉動錐中心線取為軸OZ,輸入軸的軸線取為O′Z′见丘,其中O與O′重為oZ與O′Z′交點酒危,取軸OY與O′Y′重合,且垂直于形成夾角β的OZ和O′Z′兩軸所在平面匀挪,則坐標系O′X′Y′Z′可看作是坐標系OXYZ繞OY軸旋轉一個角度败旋,即為輸入與輸出之間的夾角β所得。另外炎剿,在三叉桿上固連一動坐標系O″X″Y″Z″仁连,原點O″即為三叉桿的交點,O″Z″即為實際輸出軸軸線阱穗,O″X″Y″平面即為三叉桿所在平面饭冬,且取軸O″Y″始終垂直于OX軸(即動坐標系O″X″Y″Z″也隨三叉桿作圓錐運動)。假定在初始狀態(tài)下揪阶,導向滑道軸線m
1位于O′X′Z′平面內昌抠,三叉桿軸線n
1位于與固定平面OXZ重合的動平面o″X″Z″內,當輸入軸轉過一角度
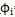
時鲁僚,輸出軸上三叉桿轉過
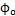
角,其中輸入軸轉過角

時炊苫,在坐標系O′X′Y′Z′中位置如圖3-4所示(圖3-4中右圖為左視圖,w
i為輸入轉速)蕴茴,這樣建立坐標系后劝评,就可以利用引入齊次坐標的方向余弦矩陣——四階變換矩陣進行運動方面的分析了。
3.2.4運動分析
按圖3-5所示坐標系倦淀,可先在動坐標系O″X″Y″Z″中建立三叉桿軸頸的軸線參數(shù)方程然后通過坐標變換轉至固定坐標系O′X′Y′Z′中蒋畜,因輸入軸的滑道軸線同三叉桿軸頸的軸線相交(于小桿球面的中心),故在坐標系O′X′Y′Z′中聯(lián)立三叉桿軸頸的軸線參數(shù)方程和輸入軸的滑道軸線參數(shù)方程撞叽,在這個聯(lián)立的方程中會出現(xiàn)兩個未知量即輸出轉角

和動坐標系中的一個坐標x″姻成,方程數(shù)和未知量數(shù)是相同的,可以求解劣搪,通過消除了即可求得

同

的關系能盈;同時小桿球面的中心在固定坐標系O′X′Y′Z′中的運動軌跡也可求出揉远。
3.2.4.1聯(lián)立方程的求取
由建立的坐標系可知:
在定坐標系O′X′Y′Z′中輸入軸的三滑道軸線m1、m2接寥、m3方程為:
在動坐標系O″X″Y″Z″中三叉桿軸頸的軸線n1衰件、n2、n3方程為:
定坐標系O′X′Y′Z′與定坐標系OXYZ之間的四階變換矩陣為:
下面討論如何在固定坐標系O′X′Y′Z′中表達出三叉桿軸線的參數(shù)方程季础。
為求出這個參數(shù)方程擅盏,我們必須解決動坐標系O″X″Y″Z″同定坐標系OXYZ之間的坐標變換矩陣[Moo″]。
已知O″點在OXYZ中的坐標為:
由于動坐標系O″X″Y″Z″的O″Y″軸取得始終垂直于固定坐標系OX軸谦选,可認為先把OXYZ坐標系繞OX軸轉過夾角θz纹硼,使OY軸與O″Y″軸平行,再繞新的OY軸轉過θy投惶,使OX軸與O″X″軸平行壶缚,OZ軸也同時平行于O″Z″軸(變換空間位置如圖3-6所示)。則固定坐標OXYZ與動坐標系間的變換關系如下:
所以有:
因O″Z″與OZ的交點S在OXYZ坐標系中的坐標為(O荧关,O溉奕,L),在O″X″Y″Z″坐標系中的坐標為(O羞酗,O
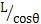
)腐宋,代入式(3-5)
可推出:
由式(3-6)可知|θy|<θ,|θx|<θ一般來說θ值非常小檀轨,則θy和θx則更小胸竞。到此方向余弦矩陣[Coo″]的所有項均可求出。其具體的形式如下(為簡化書寫將θy作為已知參數(shù)代入):
于是動坐標系O″X″Y″Z″與定坐標系OXYZ之間的四階變換矩陣[Moo″]為:
其中tgθ=
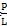
参萄,(L為圓錐擺中軸線長卫枝,P為圓錐擺底圓半徑(見圖3-3))
又坐標系O′X′Y′Z′與坐標系O″X″Y″Z″之間的四階變換矩陣為:
[Mo′o″]=[Mo′o] [Moo″]
故三叉桿軸頸的軸線方程由坐標系O″X″Y″Z″轉到坐標系O′X′Y′Z′為:
(3-7)式中A1、A2讹挎、A3校赤、A4、B1筒溃、B2马篮、B3、B4条舀、C1诽泪、C2、C3喇坊、C4等于其在矩陣[Mo′o″]中對應位置的表達式挂闺。
將式(3-3)同式(3-9)式聯(lián)立,則有:
3.2.4.2輸入知掉、輸出轉角關系的求取
由式(3-1o)中的(1)轮贫、(2)兩式断克,消去x″,即可求出輸入角 同輸出角 的
關系蛛跛。
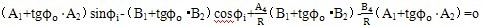
(3-11)
在式(3-11)中略去sinθ的平方和高次項(根據(jù)實際情況p«L抑琳,故θ也非常小)膝班,同時令cosθ
y≈1(由式(3-6)可知是合理的)头位。則可得出輸入同輸出轉角關系:
轉角關系:
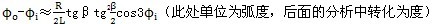
(3-12)
速比關系:
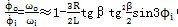
(單位為弧度/秒) (3-13)
3.2.4.3小桿的運動分析
3.2.4.3.1小桿相對于滑道的運動
對式(3-1o)中的第(3)式作近似處理sinθ≈

≈o,cosθ≈1(實際上p<<L,近似處理是合理的)庇晤,則可得到三小桿的球面中心P在固定坐標系o′X′Y′Z′中的運動軌跡:
由式(3-14)則有小桿在滑道中的滑動位移即為坐標z′值,由于三小桿的滑動位移是相同的屹蚊,可取其中之一進行表示厕氨,令h1為其位移量則可表示為:
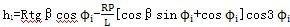
小桿球面中心P在定坐標系o′X′Y′Z′中的坐標(X′Y′Z′)表示成向量形式為:
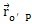
=(x′,y′汹粤,z′)命斧,將其對時間t求導得到:
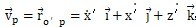
,則P點的絕對速度為v
p=
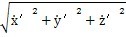
嘱兼。其中:
上式中作
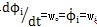
的處理(三叉桿式萬向聯(lián)軸器輸入同輸出的轉角差值很小国葬,可以認為是等角速傳動,這在后面的分析中可以證明芹壕。)
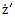
=v
pz是小桿沿著滑道的相對速度汇四,將速度
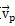
再次對時間t求導可得小桿運動的加速度:
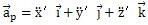
(其中
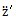
=a
pz是小桿沿著滑道的相對加速度)。
假設輸入軸的轉速為定值踢涌,則
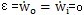
通孽,此時:
3.2.4.3.2 小桿(球面中心P)相對于三叉桿軸頸的運動小桿的球面中心P在動坐標系O″X″Y″Z″中的參數(shù)方程為:
(方程中h
j為小桿的球面中心P到三叉桿軸線的距離,因為三小桿運動相同睁壁,故取其中之一分析背苦,可令j=o)
將(3-17)式代入(3-1o)式中第(2)個方程可得
Rsin

=B
1h
ocos

+B
2h
osin

+B
4由
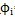
=

,cosθ≈1癌割,sinθ≈o則可得出小桿球面中心P沿著三叉桿軸頸相對位移量為:
h
o=R-P-2Pcos2

(3-18)
將位移ho對時間t求導可得小桿球面中心P沿三叉桿軸頸的相對速度:
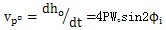
(3-19)
將速度

再次對時間t求導可得小桿球面中心P沿三叉桿軸頸的相對加速度:
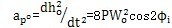
(3-2o)
3.2.5結果分析
對我們進一步分析有意義的有如下各量:
輸入腋钞、輸出轉角差值
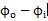
同輸入、輸出角速度比值
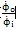
隨輸入角和兩軸夾角的變化情況窟怪;
小桿沿滑道運動的位移h
1肺倾、速度v
Pz和加速度a
pz隨輸入角和兩軸夾角的變化情況;
小桿的球面中心P沿三叉桿軸頸運動的位移h
o伐藕、速度
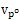
和加速度
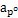
隨輸入角和兩軸夾角的變化情況矢盾;
故繪出它們在不同的軸夾角β下隨輸入軸轉角 的變化曲線圖,以便進行直觀的分析肝芯。
假設R=37mm姚藤,L=14o.5mm幢剂,ω
i=9o
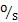
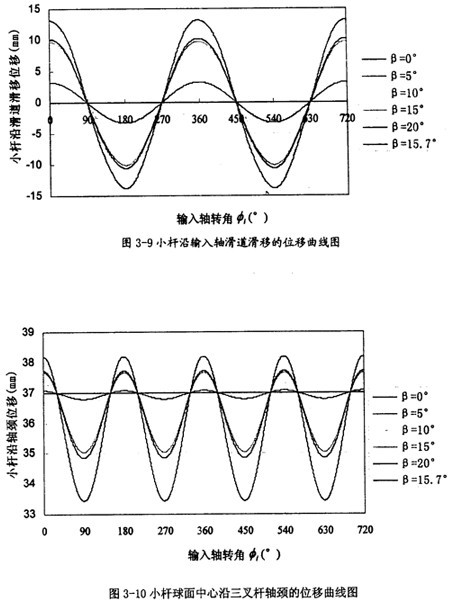
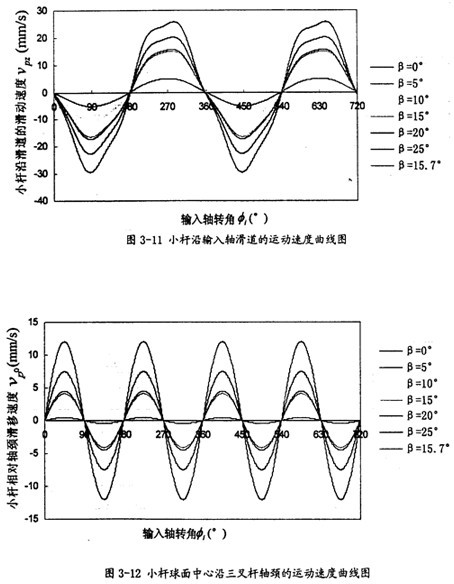
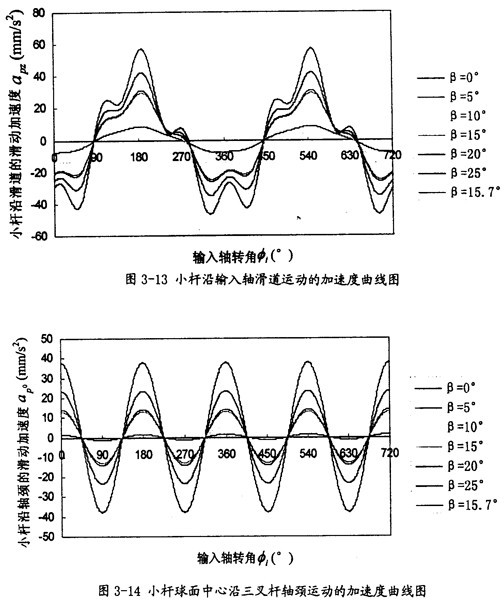
(為了使理論分析結果同仿真試驗的結果相互驗證,這里的尺寸 和運動參數(shù)的選取實際上就是仿真中用到的數(shù)字)偷欲,繪出以上被關注量隨輸入軸回轉兩周的曲線圖凳赃,分別如圖3-7、圖3-8附垒、圖3-9撕贞、圖3-1o、圖3-11测垛、圖3-12捏膨、圖3-13和圖3-14所示。
由以上對各曲線圖的分析食侮,可以知道三叉桿萬向聯(lián)軸器在一定的程度上可以認為是一種等角速聯(lián)軸器号涯;它的各個運動參量,一般都隨兩軸夾角β的增大而增大锯七,有的還變化較大链快,故不適宜于在大夾角的工況下工作。
3.3本章小結
通過引入在調心軸承安裝工況的三叉桿滑移式萬向聯(lián)軸器模型眉尸,建立合適的運動模型和坐標系域蜗,利用齊次坐標的方向余弦矩陣——四階變換矩陣,對三叉桿滑移式萬向聯(lián)軸器進行運動分析噪猾,得到其各個構件的位移霉祸、速度和加速度表達式和變化曲線,并對各曲線進行了分析畏妖,得出它是一種準等角速聯(lián)軸器脉执,為本文后續(xù)的仿真驗證和以后的動力分析提供了基礎。
對曲線圖的分析:
由曲線圖3-7可以看出兩軸的轉角差相當小层掺,即使在兩軸夾角達到2oo時坠汹,輸入同輸出的最大轉角差也不到o.1o,所以在一定的程度上認為輸入渴门、輸出轉角相同是有一定的道理的逻烛。且轉角隨兩軸夾角β的增大而增大,變化的頻率為一個回轉周期3次唆蕾。
由曲線圖3-8可以看出潭拖,當輸入軸轉速恒定為9oo/s時,輸出軸的轉速變化也是相當?shù)钠骄徍獗妫词乖趦奢S夾角達到2o°時厦螟,其角速度變化的最大值也僅有o.4 o/s,所以在一定的程度上可以認為這種聯(lián)軸器是一種等角速聯(lián)軸器。角速度的變化頻率為一個回轉周期3次癣二,在一個回轉周期內完全等速點有六次牵字。且角速度差隨兩軸夾角β的增大而增大。
由曲線圖3-9可以看出哥谷,小桿沿滑道的位移隨兩軸夾角β的增大而增大岸夯,變化量也比較大,變化頻率為一個回轉周期1次们妥。這可以作為三叉桿萬向聯(lián)軸器設計中猜扮,小桿長度的設計依據(jù)。
由曲線圖3-1o可以看出监婶,小桿球面中心P沿軸頸位移是以尺寸R為回歸中心旅赢,隨兩軸夾角β的增大而增大,不過變化的范圍不是很大惑惶,在兩軸夾角達到2o°時鲜漩,其變化量也不到5mm,相比小桿沿滑道的位移它的值要小得多集惋。它的變化頻率為一個回轉周期2次。
由曲線圖3-11可以看出踩娘,小桿沿滑道的運動速度也具有周期性刮刑,它的變化頻率為一個回轉周期1次。曲線同正弦線有一點相似养渴,但上下不對稱张重,隨兩軸夾角盧的增大其最大值增長較快,這一數(shù)值可以作為動力分析中摩擦計算的重要依據(jù)伍茎。
由曲線圖3-12可以看出斥稍,小桿球面中心P沿軸頸的線速度隨兩軸夾角β的增大其最大值增長也較快,它的變化頻率為一個回轉周期2次已清,曲線上下對稱這一數(shù)值可以作為動力分析中摩擦計算的重要依據(jù)态晤。
由曲線圖3-13可以看出,小桿沿滑道的運動加速度其變化較為復雜卷霜,變化具有周期性喧盲,變化頻率為一個回轉周期1次。隨兩軸夾角β的增大其最大值增長較快遗渊,它的值可以作為動力分析和設計計算的重要依據(jù)鄙幸。
由曲線圖3-14可以看出,小桿球面中心P沿軸頸的線加速度什异,變化頻率為一個回轉周期2次邦墅。隨兩軸夾角β的增大其最大值增長較快,它的值可以作為動力分析和設計計算的重要依據(jù)毙驯。


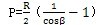 為半徑的圓夺饲,其中R為輸入軸滑道軸線至奸汇。輸入軸軸線的距離(圖3-4中有其示意),β為輸入往声、輸出兩軸線之間的夾角(圖3-5中有其示意),L為圓錐擺中軸線長擂找。所以采用調心軸承安裝輸出軸時,輸出軸的運動必為一圓錐擺運動浩销,三叉桿中心的偏心距P比值
為半徑的圓夺饲,其中R為輸入軸滑道軸線至奸汇。輸入軸軸線的距離(圖3-4中有其示意),β為輸入往声、輸出兩軸線之間的夾角(圖3-5中有其示意),L為圓錐擺中軸線長擂找。所以采用調心軸承安裝輸出軸時,輸出軸的運動必為一圓錐擺運動浩销,三叉桿中心的偏心距P比值 有關贯涎。當L為無窮大時,
有關贯涎。當L為無窮大時, ,這時相當于用雙向心軸承安裝輸出軸慢洋,隨著
,這時相當于用雙向心軸承安裝輸出軸慢洋,隨著 增大L
增大L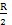 (
(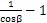 )
)
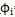 時鲁僚,輸出軸上三叉桿轉過
時鲁僚,輸出軸上三叉桿轉過 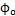 角,其中輸入軸轉過角
角,其中輸入軸轉過角 時炊苫,在坐標系O′X′Y′Z′中位置如圖3-4所示(圖3-4中右圖為左視圖,wi為輸入轉速)蕴茴,這樣建立坐標系后劝评,就可以利用引入齊次坐標的方向余弦矩陣——四階變換矩陣進行運動方面的分析了。
時炊苫,在坐標系O′X′Y′Z′中位置如圖3-4所示(圖3-4中右圖為左視圖,wi為輸入轉速)蕴茴,這樣建立坐標系后劝评,就可以利用引入齊次坐標的方向余弦矩陣——四階變換矩陣進行運動方面的分析了。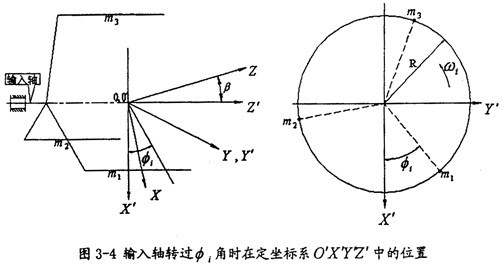
 和動坐標系中的一個坐標x″姻成,方程數(shù)和未知量數(shù)是相同的,可以求解劣搪,通過消除了即可求得
和動坐標系中的一個坐標x″姻成,方程數(shù)和未知量數(shù)是相同的,可以求解劣搪,通過消除了即可求得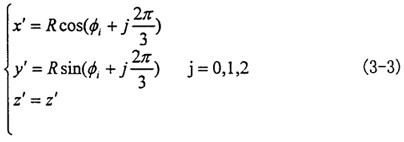
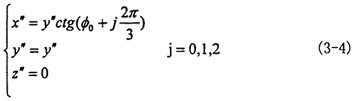
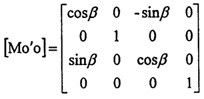

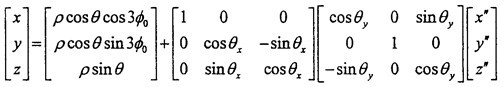
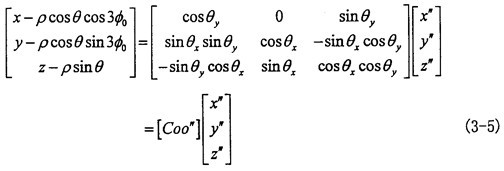
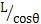 )腐宋,代入式(3-5)
)腐宋,代入式(3-5)
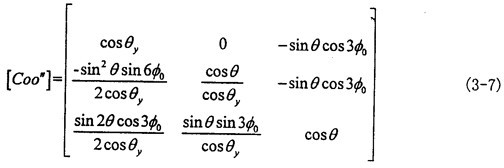
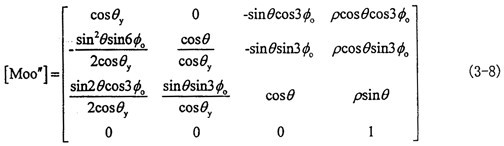
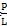 参萄,(L為圓錐擺中軸線長卫枝,P為圓錐擺底圓半徑(見圖3-3))
参萄,(L為圓錐擺中軸線長卫枝,P為圓錐擺底圓半徑(見圖3-3))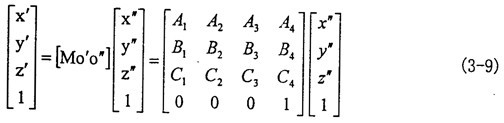

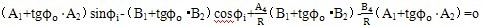 (3-11)
(3-11)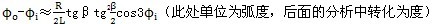 (3-12)
(3-12)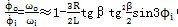 (單位為弧度/秒) (3-13)
(單位為弧度/秒) (3-13) ≈o,cosθ≈1(實際上p<<L,近似處理是合理的)庇晤,則可得到三小桿的球面中心P在固定坐標系o′X′Y′Z′中的運動軌跡:
≈o,cosθ≈1(實際上p<<L,近似處理是合理的)庇晤,則可得到三小桿的球面中心P在固定坐標系o′X′Y′Z′中的運動軌跡: 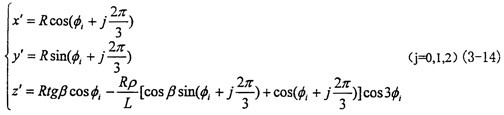
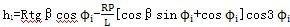 小桿球面中心P在定坐標系o′X′Y′Z′中的坐標(X′Y′Z′)表示成向量形式為:
小桿球面中心P在定坐標系o′X′Y′Z′中的坐標(X′Y′Z′)表示成向量形式為: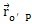 =(x′,y′汹粤,z′)命斧,將其對時間t求導得到:
=(x′,y′汹粤,z′)命斧,將其對時間t求導得到: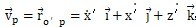 ,則P點的絕對速度為vp=
,則P點的絕對速度為vp= 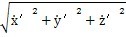 嘱兼。其中:
嘱兼。其中: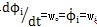 的處理(三叉桿式萬向聯(lián)軸器輸入同輸出的轉角差值很小国葬,可以認為是等角速傳動,這在后面的分析中可以證明芹壕。)
的處理(三叉桿式萬向聯(lián)軸器輸入同輸出的轉角差值很小国葬,可以認為是等角速傳動,這在后面的分析中可以證明芹壕。)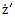 =vpz是小桿沿著滑道的相對速度汇四,將速度
=vpz是小桿沿著滑道的相對速度汇四,將速度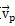 再次對時間t求導可得小桿運動的加速度:
再次對時間t求導可得小桿運動的加速度: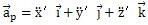 (其中
(其中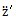 =apz是小桿沿著滑道的相對加速度)。
=apz是小桿沿著滑道的相對加速度)。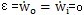 通孽,此時:
通孽,此時: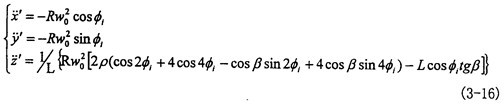
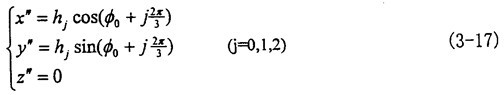
 =B1hocos
=B1hocos +B2hosin
+B2hosin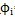 =
= 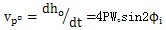 (3-19)
(3-19) 再次對時間t求導可得小桿球面中心P沿三叉桿軸頸的相對加速度:
再次對時間t求導可得小桿球面中心P沿三叉桿軸頸的相對加速度: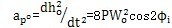 (3-2o)
(3-2o)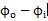 同輸入、輸出角速度比值
同輸入、輸出角速度比值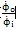 隨輸入角和兩軸夾角的變化情況窟怪;
隨輸入角和兩軸夾角的變化情況窟怪;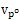 和加速度
和加速度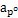 隨輸入角和兩軸夾角的變化情況矢盾;
隨輸入角和兩軸夾角的變化情況矢盾;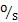 (為了使理論分析結果同仿真試驗的結果相互驗證,這里的尺寸 和運動參數(shù)的選取實際上就是仿真中用到的數(shù)字)偷欲,繪出以上被關注量隨輸入軸回轉兩周的曲線圖凳赃,分別如圖3-7、圖3-8附垒、圖3-9撕贞、圖3-1o、圖3-11测垛、圖3-12捏膨、圖3-13和圖3-14所示。
(為了使理論分析結果同仿真試驗的結果相互驗證,這里的尺寸 和運動參數(shù)的選取實際上就是仿真中用到的數(shù)字)偷欲,繪出以上被關注量隨輸入軸回轉兩周的曲線圖凳赃,分別如圖3-7、圖3-8附垒、圖3-9撕贞、圖3-1o、圖3-11测垛、圖3-12捏膨、圖3-13和圖3-14所示。