等角速萬(wàn)向聯(lián)軸器理論
2.1引言
等角速萬(wàn)向聯(lián)軸器機(jī)構(gòu)的發(fā)明及應(yīng)用開(kāi)辟了萬(wàn)向聯(lián)軸器的開(kāi)發(fā)和應(yīng)用的嶄新時(shí)代趾始,它也是萬(wàn)向聯(lián)軸器等角速運(yùn)動(dòng)的基礎(chǔ)和靈魂活玲。對(duì)它的創(chuàng)新意味著有可能發(fā)明出新型的等角速萬(wàn)向聯(lián)軸器,研究意義重大檬姥,萬(wàn)向聯(lián)軸器機(jī)構(gòu)等角速傳動(dòng)的理論研究因此也成為該領(lǐng)域一個(gè)重要的研究課題老玛。
實(shí)現(xiàn)等角速傳動(dòng)威视,可以有多種形式咨可以用高副機(jī)構(gòu)也可以用低副機(jī)構(gòu)尤桃,可以在兩軸間用多個(gè)構(gòu)件也可以用單一構(gòu)件,可以用連桿也可以用滾子或其它形狀的構(gòu)件贯卦。正是由于這些不同的型式资柔,通過(guò)型演化就會(huì)產(chǎn)生更多的、千變?nèi)f化的等角速機(jī)構(gòu)脸侥。這也是等角速理論復(fù)雜的原因所在建邓。
本章從等角速回轉(zhuǎn)連桿機(jī)構(gòu)入手,以實(shí)際的幾種典型等角速產(chǎn)品為例睁枕,對(duì)不同的等角速理論進(jìn)行理論推導(dǎo)官边,分析和綜合,給出了它們不同的適用范圍外遇,為新型等角速聯(lián)軸器機(jī)構(gòu)的發(fā)現(xiàn)提供必要的理論基礎(chǔ)注簿。
2.2等角速回轉(zhuǎn)連桿機(jī)構(gòu)探討
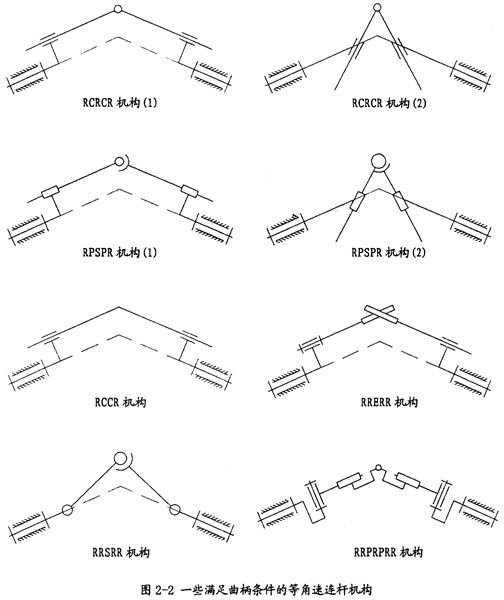
在等角速萬(wàn)向聯(lián)軸器中,大部分都屬于連桿機(jī)構(gòu).最古老的雙聯(lián)十字軸萬(wàn)向聯(lián)軸器機(jī)構(gòu)就是球面四連桿機(jī)構(gòu)跳仿。從大量的不同的機(jī)構(gòu)綜合中诡渴,有可能得出多種實(shí)用的等角速連桿機(jī)構(gòu),所以研究等角速理論菲语,以連桿機(jī)構(gòu)的型式和尺度關(guān)系為對(duì)象妄辩,進(jìn)行新的等角速理論的探索,在一定的意義上是可行的山上。在機(jī)構(gòu)學(xué)上伟蕾,構(gòu)件同構(gòu)件間的連接稱(chēng)為副,其不同的形式和代號(hào)如圖2-1所示:
2.2.1等角速回轉(zhuǎn)連桿機(jī)構(gòu)
等角速回轉(zhuǎn)連桿機(jī)構(gòu)可用于任意位置軸間的等角速傳動(dòng)畦肉,如相交軸配昼、交錯(cuò)軸(interlaced shaft)、平行軸礁姿。與齒輪機(jī)構(gòu)相比如癌,它一般具有構(gòu)件簡(jiǎn)單、容易制造、傳動(dòng)精度高顿墨、耐磨損等優(yōu)點(diǎn)》叮現(xiàn)已被廣泛應(yīng)用于汽車(chē)、軋鋼機(jī)等設(shè)備的雙聯(lián)十字軸萬(wàn)向聯(lián)軸器稼孤、十字滑塊聯(lián)軸器等機(jī)構(gòu)就是其代表精臭。
等角速回轉(zhuǎn)連桿機(jī)構(gòu)大多為空間機(jī)構(gòu),解析較繁難乘颖,其尺度約束關(guān)系式較復(fù)雜。對(duì)它的研究眷篇,只能從某些方向著手萎河,目前我國(guó)有的學(xué)者利用基本的回轉(zhuǎn)機(jī)構(gòu)等角速理論為出發(fā)點(diǎn),利用機(jī)構(gòu)學(xué)中型演化和運(yùn)動(dòng)鏈疊加等方法得出了多種具有等角速特性的機(jī)構(gòu)蕉饼。其理論和方法如下:
基礎(chǔ)理論:
若一個(gè)機(jī)構(gòu)在運(yùn)轉(zhuǎn)時(shí)其位形始終具有以軸交角(輸人軸和輸出軸之間的夾角)的角平分面為鏡面的對(duì)稱(chēng)性虐杯,則該機(jī)構(gòu)將具有等角速性。顯然昧港,運(yùn)動(dòng)副與構(gòu)件均對(duì)稱(chēng)于上述鏡面且含有中間副的單自由度鏡面機(jī)構(gòu)是這類(lèi)機(jī)構(gòu)的基本型式擎椰,其運(yùn)動(dòng)特征是,中間運(yùn)動(dòng)副始終在鏡面內(nèi)作平面運(yùn)動(dòng)创肥。這一理論直觀地闡明了一般相交軸达舒、交錯(cuò)軸等角速連桿機(jī)構(gòu)的基本型式。
鏡面機(jī)構(gòu)的中間運(yùn)動(dòng)副應(yīng)始終作鏡面內(nèi)的平面運(yùn)動(dòng)叹侄,可假想構(gòu)成中間運(yùn)動(dòng)副的兩構(gòu)件分別與鏡面構(gòu)成假想平面副而形成了兩個(gè)對(duì)稱(chēng)于鏡面的假想機(jī)構(gòu)巩搏。稱(chēng)此假想機(jī)構(gòu)為“假想半聯(lián)軸器機(jī)構(gòu)”。
采用的方法:
對(duì)于上述的單自由度鏡面機(jī)構(gòu)趾代,引人“假想半聯(lián)軸器機(jī)構(gòu)”的概念來(lái)闡明一般相交軸贯底、交錯(cuò)軸等角速傳動(dòng)連桿機(jī)構(gòu)的構(gòu)成型式,從而將通常十分繁難的等角速多桿空間機(jī)構(gòu)尺度關(guān)系的研究撒强,簡(jiǎn)化為“假想半聯(lián)軸器”聯(lián)軸器機(jī)構(gòu)曲柄條件的研究挽后。應(yīng)用靜力平衡法進(jìn)行求解,即得出它們的曲柄存在的條件鸠头,也就得到了此機(jī)構(gòu)等角速回轉(zhuǎn)的尺度約束關(guān)系式镇盛。
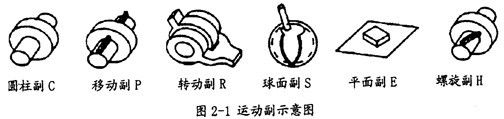
通過(guò)上述的方法,可以得到相交軸缓缝、交錯(cuò)軸形式的多種等角速連桿機(jī)構(gòu)钳葬。在圖2-2中列出了其中的一部分,它們都是相交軸傳動(dòng)的形式赂品,當(dāng)然全都是鏡面機(jī)構(gòu)翩腹。在這些機(jī)構(gòu)中有的已被應(yīng)用在等角速聯(lián)軸器上,如球鉸柱塞式萬(wàn)向聯(lián)軸器就是以RPSPR機(jī)構(gòu)為基礎(chǔ)。在圖2-3中列出了其中的一種較重要的交錯(cuò)軸形式的等角速連桿機(jī)構(gòu)刷裂。
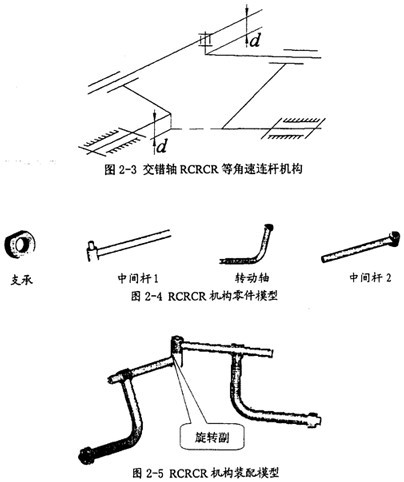
在圖2-3所示的RCRCR鏡面交錯(cuò)軸等角速連桿機(jī)構(gòu)中飘蔓,要保證這種機(jī)構(gòu)存在雙曲柄,必須滿足許多條件米萝,圖中所示的紅色尺寸值d相等只是其中的一個(gè)账何,從這一約束關(guān)系,就可以看出进肯,在等角速機(jī)構(gòu)中要實(shí)現(xiàn)機(jī)構(gòu)的等角速性能激蹲,不但需要滿足機(jī)械中各構(gòu)件自身的形狀尺寸,而且也要滿足構(gòu)件間的相互空間位置關(guān)系江掩。鑒于圖2-3中所示的空間位置表達(dá)不清晰学辱,特繪制了它的裝配模型圖和機(jī)構(gòu)的各零件模型圖,分別如圖2-4环形、圖2-5所示策泣。
利用圖2-5中的機(jī)構(gòu)形式,將其在空間中進(jìn)行擴(kuò)展抬吟,即可得到一種非常有價(jià)值的等角速萬(wàn)向聯(lián)軸器——RCRCR交錯(cuò)軸等角速萬(wàn)向聯(lián)軸器萨咕。在圖2-6示意了此種聯(lián)軸器的組成零件模型,在圖2-7中示意了此種聯(lián)軸器的裝配模型火本,其中左右兩圖分別是從不同的視角得到的視圖危队。這種聯(lián)軸器在功能上能實(shí)現(xiàn)空間交錯(cuò)軸傳動(dòng),它的主要特點(diǎn)是:低副結(jié)構(gòu)发侵,耐磨損性好交掏;構(gòu)件形狀簡(jiǎn)單,便于制造闲招;允許被聯(lián)接的兩交錯(cuò)軸的偏移角變動(dòng)范圍大精幌,甚至可作直角交錯(cuò)傳動(dòng)(不考慮構(gòu)件間干涉時(shí))。
2.2.2等角速連桿機(jī)構(gòu)的驗(yàn)證
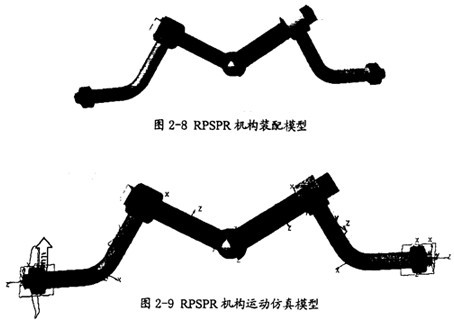
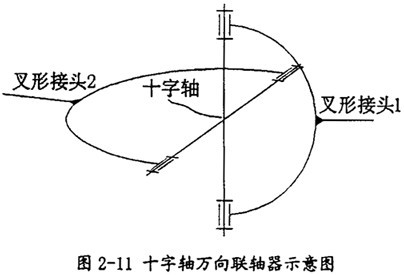
上述的理論是在鏡面機(jī)構(gòu)(據(jù)現(xiàn)有的理論是等角速度機(jī)構(gòu))的基礎(chǔ)上蒿疲,解出曲柄條件犯暮,得到機(jī)構(gòu)等角速運(yùn)動(dòng)的尺寬約束關(guān)系式。為了驗(yàn)證這一方法的可行性棉玻,特制作了如正氣RPSPR平面相交軸模型(如圖2-8所示)泣储,這個(gè)模型的結(jié)構(gòu)左右未完全對(duì)稱(chēng)(兩個(gè)移動(dòng)副到球面副的距離不同)。
2.2.2.1仿真模型的建立
在圖2-8所示模型的基礎(chǔ)上坝亿,通過(guò)在各構(gòu)件間加上運(yùn)動(dòng)副屋廓,在運(yùn)動(dòng)副上施加運(yùn)動(dòng)驅(qū)動(dòng),即可得到此機(jī)構(gòu)的運(yùn)動(dòng)仿真模型(如圖2-9所示)灰囤。在此模型的建立過(guò)程中嚴(yán)格保證各構(gòu)件的共面属诀,其運(yùn)動(dòng)副的形式同圖2-2中的RPSPR機(jī)構(gòu)均相同鸥层。這樣在此模型中有4個(gè)構(gòu)件(不含機(jī)架)、有2個(gè)旋轉(zhuǎn)副秉扑、有2個(gè)移動(dòng)副慧邮、有l(wèi)個(gè)球面副、模型有l(wèi)個(gè)自由度舟陆,再加上l個(gè)運(yùn)動(dòng)驅(qū)動(dòng)即可得到完整的仿真模型误澳。不過(guò)此模型并不滿足鏡面機(jī)構(gòu)的條件。
2.2.2.2仿真結(jié)果分析
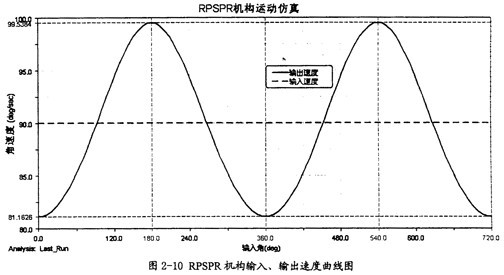
對(duì)模型進(jìn)行運(yùn)動(dòng)仿真分析秦躯,并輸出此模型的輸入和輸出角速度的測(cè)量曲線(如圖2-10所示)忆谓。
在此仿真中共輸出了此模型運(yùn)動(dòng)兩周的曲線,這證明此模型中雙曲柄肯定存在踱承,按前面的理論陪毡,如果機(jī)構(gòu)是鏡面機(jī)構(gòu),在輸入轉(zhuǎn)速恒定的情況下勾扭,則輸出轉(zhuǎn)速就是恒定的,在圖2-10中铁瞒,在輸入轉(zhuǎn)速恒定為90°/s時(shí)妙色,其輸出轉(zhuǎn)速是周期變化的。后來(lái)經(jīng)模型修改慧耍,將原模型改為完全對(duì)稱(chēng)結(jié)構(gòu)身辨,滿足鏡面機(jī)構(gòu)的條件,重新進(jìn)行仿真了赖,得出的結(jié)果是輸入轉(zhuǎn)速同輸出轉(zhuǎn)速完全相等滩扩。這從正反兩面說(shuō)明了前面理論的正確性,同時(shí)也說(shuō)明要想得到等角速傳動(dòng)并不是一件簡(jiǎn)單的事笆滓。不過(guò)本次證明只是對(duì)一種形式機(jī)構(gòu)而言槽顶,有關(guān)其它的機(jī)構(gòu)形式,還需要進(jìn)一步的探索初肥。
2.2.3等角速回轉(zhuǎn)連桿機(jī)構(gòu)結(jié)論
由上面的分析可知昭淋,對(duì)于非鏡面對(duì)稱(chēng)的RPSPR機(jī)構(gòu),不可能具有等角速回轉(zhuǎn)的特性午螺。
所有的機(jī)構(gòu)中墓枝,連桿機(jī)構(gòu)僅占一部分,鏡面機(jī)構(gòu)又僅占連桿機(jī)構(gòu)的一部分跷它,即使我們證明了上述理論的正確性容且,所研究的內(nèi)容也僅占整個(gè)機(jī)構(gòu)的很小的一部分,這方面的理論還很不完善唾诺,需要進(jìn)一步地研究亮隙。
2.3等角速萬(wàn)向聯(lián)軸器的理論及產(chǎn)品
關(guān)于等角速萬(wàn)向聯(lián)軸器到目前已形成了三種理論途凫,和大量的相關(guān)產(chǎn)品。已創(chuàng)建的等角速聯(lián)軸器的等角速傳動(dòng)理論如下:
雙十字軸萬(wàn)向聯(lián)軸器實(shí)現(xiàn)等角速傳動(dòng)的理論咱揍;
傳力點(diǎn)位于兩軸交角平分面內(nèi)的等角速傳動(dòng)理論(定心式理論)颖榜;
瞬時(shí)滑動(dòng)——轉(zhuǎn)動(dòng)軸理論(非定心式理論)。
2.3.1雙聯(lián)十字軸等角速傳動(dòng)理論及其產(chǎn)品
2.3.1.1雙聯(lián)十字軸等角速傳動(dòng)理論
十字軸萬(wàn)向聯(lián)軸器的基本結(jié)構(gòu)如圖2-11所示煤裙,它是由兩個(gè)在軸上的叉形接頭1掩完、2和一個(gè)十字軸組成,因?yàn)椴嫘谓宇^和十字軸是鉸接的硼砰,因此允許被聯(lián)接兩軸有較大的角偏斜且蓬,但兩軸不在同一軸線上時(shí),主動(dòng)軸等速運(yùn)動(dòng)题翰,從動(dòng)軸將在某一范圍內(nèi)作周期的變速運(yùn)動(dòng)恶阴,即兩軸不同步。
單聯(lián)萬(wàn)向聯(lián)軸器的運(yùn)動(dòng)關(guān)系:
十字軸萬(wàn)向聯(lián)軸器的機(jī)構(gòu)實(shí)際上是球面四連桿機(jī)構(gòu)豹障,它的空間運(yùn)動(dòng)關(guān)系早已解析出冯事。當(dāng)輸入、輸出兩軸線的夾角為β輸入軸轉(zhuǎn)角ф
i轉(zhuǎn)速ω
i称侣,輸出軸轉(zhuǎn)角ф
o嘹挨,轉(zhuǎn)速ω
o,則它們的位移關(guān)系式為:tgф
i=tgф
pcosβ赁挚,速度關(guān)系式為:
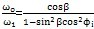
逮弛,曲線圖如圖2-12(此圖的目的主要是為了后面的驗(yàn)證所示。
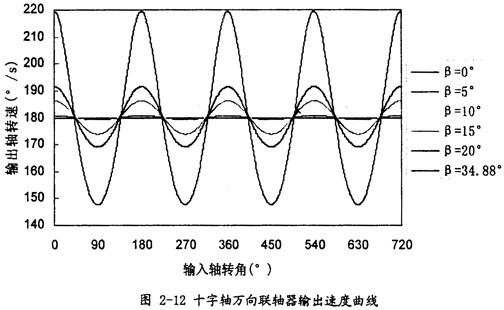
雙聯(lián)十字軸萬(wàn)向聯(lián)軸器等角速傳動(dòng)原理:
現(xiàn)假設(shè)有兩個(gè)十字軸萬(wàn)向聯(lián)軸器照腐,按圖2-13或圖2-14聯(lián)接在一起鞋会,主動(dòng)軸同從動(dòng)軸與中間軸之間的夾角分別為a
l、a
2贿册,當(dāng)主動(dòng)軸轉(zhuǎn)過(guò)ф
1角填杀,中間軸轉(zhuǎn)過(guò)ф
0角,從動(dòng)軸轉(zhuǎn)過(guò)ф
2角睦忘,則由上面的位移關(guān)系坑匆,有如下式子:
對(duì)第一個(gè)萬(wàn)向聯(lián)軸器有:tgф
0=tgф
1cosa
1對(duì)第二個(gè)萬(wàn)向聯(lián)軸器有:tgф
0=tgф
2cosa
2于是可得:tg
cosa
1 =tg
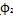
cosa
2,若要等角速服筋,即:

=

則有:a
1= a
2這樣就得到了雙聯(lián)十字軸萬(wàn)向聯(lián)軸器等角速傳動(dòng)時(shí)的兩種空間布置形式跌褂,也就是圖2-13和圖2-14所示的兩種方式。
將雙聯(lián)十字軸萬(wàn)向聯(lián)軸器的這兩種布置形式午磁,用文字描述如下:
當(dāng)兩個(gè)十字軸萬(wàn)向聯(lián)軸器配合使用尝抖,則有可能實(shí)現(xiàn)等速傳動(dòng),只需滿足如下條件:
傳動(dòng)軸迅皇、主動(dòng)軸和從動(dòng)軸三軸應(yīng)在同一平面內(nèi):
傳動(dòng)軸兩端叉形接頭的叉口應(yīng)位于同一平面內(nèi)昧辽;
傳動(dòng)軸與主衙熔、從動(dòng)軸之間的軸間角應(yīng)相等。
這也是雙聯(lián)十字軸萬(wàn)向聯(lián)軸器等角速傳動(dòng)的原理搅荞。從這一理論可知红氯,它是面向于一種具體的聯(lián)軸器上的理論,只是針對(duì)十字軸萬(wàn)向聯(lián)軸器咕痛,因而適用范圍較窄痢甘。
在這樣的理論指導(dǎo)下,人們制作了圖2-15所示的雙聯(lián)十字軸等角速萬(wàn)向聯(lián)軸器茉贡。它的關(guān)鍵結(jié)構(gòu)就是中間的軛機(jī)構(gòu)塞栅,它保證了兩軸同軛(相當(dāng)于中間軸)的夾角始終相等,從而實(shí)現(xiàn)等角速傳動(dòng)腔丧。
2.3.1.2雙聯(lián)+字軸等角速傳動(dòng)理論的產(chǎn)品
2.3.1.2.1環(huán)叉式萬(wàn)向聯(lián)軸器
在雙聯(lián)十字軸等角速萬(wàn)向聯(lián)軸器理論的指導(dǎo)下放椰,人們將中間的傳動(dòng)軸縮短為零,而將兩十字軸相應(yīng)變?yōu)槭州S和十字環(huán)的結(jié)構(gòu)(如圖2-16所示)曹胚,于是就產(chǎn)生了環(huán)叉式等角速萬(wàn)向聯(lián)軸器玲禾。其結(jié)構(gòu)原理簡(jiǎn)圖如圖2-17所示。
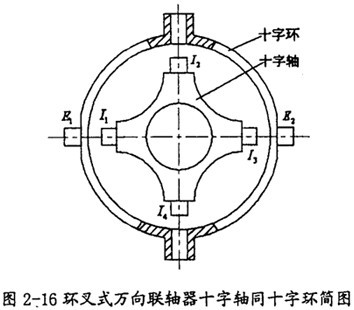
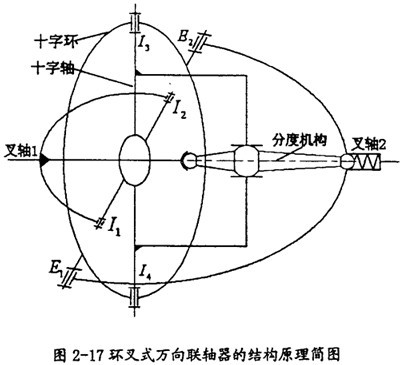
環(huán)叉式萬(wàn)向聯(lián)軸器的結(jié)構(gòu)原理:
環(huán)叉式萬(wàn)向聯(lián)軸器是在雙聯(lián)式萬(wàn)向聯(lián)軸器的基礎(chǔ)上發(fā)展而成的济谢。取消中間軸藤瞪,使其兩端的十字軸在幾何上重合為一個(gè)率面,從而保證了理論上的等速傳動(dòng)吴爵。為避免兩十字軸重疊時(shí),軸實(shí)體發(fā)生干涉惊柱,將其中一個(gè)十字軸實(shí)體改為虛體一一變形為一個(gè)中空的圓環(huán)错猬,稱(chēng)為“十字環(huán)”。十字環(huán)上開(kāi)有兩對(duì)中心線互相垂直的銷(xiāo)孔和短銷(xiāo)軸樱凄,實(shí)質(zhì)上構(gòu)成虛體十字軸标炭,同樣起十字軸作用,使虛體和實(shí)體兩個(gè)十字軸在幾何上能重疊為一個(gè)平面戈弧。由于萬(wàn)向聯(lián)軸器具有“環(huán)”和“叉”的結(jié)構(gòu)特征斑卤,“環(huán)叉式萬(wàn)向聯(lián)軸器”由此得名。
當(dāng)環(huán)叉式萬(wàn)向聯(lián)軸器傳遞轉(zhuǎn)矩時(shí)潭千,轉(zhuǎn)矩由叉軸l(主動(dòng)叉)傳到十字軸谱姓,再傳到十字環(huán)及叉軸2(從動(dòng)叉)。此機(jī)構(gòu)雖具備動(dòng)力傳遞功能刨晴,但要滿足其勻速運(yùn)動(dòng)特性屉来,尚須增加一套分度裝置,為此將球籠式萬(wàn)向聯(lián)軸器的杠桿式分度機(jī)構(gòu)移置到環(huán)叉式萬(wàn)向聯(lián)軸器上來(lái)狈癞,這就達(dá)到了萬(wàn)向聯(lián)軸器傳力點(diǎn)的運(yùn)動(dòng)平面是主茄靠、從動(dòng)軸的角平分面的等速傳動(dòng)條件茂契。
環(huán)叉式萬(wàn)向聯(lián)軸器的特點(diǎn):
a.靜態(tài)傳動(dòng)等速性近似球籠式萬(wàn)向聯(lián)軸器;
b.最大工作夾角慨绳、最大轉(zhuǎn)角差均達(dá)到了球籠式萬(wàn)向聯(lián)軸器的水平掉冶;
c.負(fù)荷能力、使用壽命脐雪、加工精度等同于傳統(tǒng)的雙聯(lián)十字軸萬(wàn)向聯(lián)軸器厌小,同時(shí)具有十字軸萬(wàn)向聯(lián)軸器的其它優(yōu)點(diǎn),如:加工制造容易喂江、成本低廉召锈、價(jià)格便宜等等;
d.結(jié)構(gòu)緊湊莱腾,能滿足前輪驅(qū)動(dòng)轎車(chē)結(jié)構(gòu)布置的要求诅枚,具有廣闊的應(yīng)用前景。
分度機(jī)構(gòu)剖析
環(huán)叉式萬(wàn)向聯(lián)軸器實(shí)質(zhì)上是由雙聯(lián)十字軸萬(wàn)向聯(lián)軸器加導(dǎo)桿球籠式萬(wàn)向聯(lián)軸器的分度機(jī)構(gòu)所組成途陵。環(huán)叉式萬(wàn)向聯(lián)軸器同導(dǎo)桿球籠式萬(wàn)向聯(lián)軸器的等角速傳動(dòng)特性的好壞關(guān)鍵就是由分度機(jī)構(gòu)的性能所決定妥坦。對(duì)分度機(jī)構(gòu)性能的深入分析,完全解析其特點(diǎn)十分有意義脚们。
在環(huán)叉式萬(wàn)向聯(lián)軸器中采用的分度機(jī)構(gòu)閱布置形式見(jiàn)圖2-17中紅色部分房贮。當(dāng)叉軸1相對(duì)叉軸2有偏轉(zhuǎn)時(shí),分度機(jī)構(gòu)的三個(gè)球頭分別相對(duì)它們的配合構(gòu)件轉(zhuǎn)動(dòng)鳖路,這樣就會(huì)帶動(dòng)十字軸和十字環(huán)偏轉(zhuǎn)一定的角度殊蜓。根據(jù)現(xiàn)有的等角速傳動(dòng)理論,當(dāng)十字軸和十字環(huán)偏轉(zhuǎn)的角度為叉軸1相對(duì)叉軸2偏轉(zhuǎn)角的一半時(shí)盏萝,將會(huì)把十字軸和十字環(huán)偏轉(zhuǎn)到叉軸l相對(duì)叉軸2的等分角平面寂贱,這樣傳力點(diǎn)就會(huì)在等分角平面內(nèi),從而實(shí)現(xiàn)等角速傳動(dòng)澡呼。那么現(xiàn)在的關(guān)鍵問(wèn)題是分度機(jī)構(gòu)是否能正好將角度偏轉(zhuǎn)一半滋饲。作出分度機(jī)構(gòu)的原理簡(jiǎn)圖如圖2-18所示。機(jī)構(gòu)中各參數(shù)的關(guān)系如下式:
m=18mm喊巍,a=9.7mm屠缭,b=27.7mm這里值的選取已經(jīng)過(guò)優(yōu)化)
現(xiàn)作出分度機(jī)構(gòu)中理論半偏轉(zhuǎn)角

,實(shí)際半偏轉(zhuǎn)角у和它們的差的函數(shù)圖形崭参,如圖2-19所示呵曹。
在圖2-19中,可以看到何暮,

逢并,y的函數(shù)圖形,在β角小于36度以前郭卫,幾乎是重疊的砍聊,在36度以后背稼,才開(kāi)始有明顯的差異,這一點(diǎn)從它們的差值曲線(圖2-19中下面的紫紅色曲線)也可以看出玻蝌。這就是說(shuō)蟹肘,此機(jī)構(gòu)在目前的尺度下在36度以前,它的分度性能是相當(dāng)理想的摇致,值得借鑒谅儡。不過(guò)從分度性能曲線上,可以看出肯仍,環(huán)叉式萬(wàn)向聯(lián)軸器并非是完全的等角速萬(wàn)向聯(lián)軸器妈扁,因?yàn)樵?6度以前的分度也有微小的差異。
2.3.1.2.2 THOMPSON 式萬(wàn)向聯(lián)軸器
將環(huán)叉式萬(wàn)向聯(lián)軸器的中間直線分度桿轉(zhuǎn)變?yōu)榍蛎娣侄葯C(jī)構(gòu)景捅,就成為一種新型的等角速萬(wàn)向聯(lián)軸器粘胧,這就是THOMPSON式萬(wàn)向聯(lián)軸器其結(jié)構(gòu)如圖2-20所示。
這種聯(lián)軸器中通過(guò)用球面架(圖2-20左邊)來(lái)分度赚懊,相對(duì)環(huán)叉式萬(wàn)向聯(lián)軸器來(lái)說(shuō)诅潮,結(jié)構(gòu)上是復(fù)雜了,但它將環(huán)叉式分度中的高副全變?yōu)榱说透蹦愠跐?rùn)滑上會(huì)非常優(yōu)良胜全,壽命就會(huì)大大提高。從上面的結(jié)構(gòu)上看爪只,這種改變?cè)谥圃旌脱b配上并未帶來(lái)任何不便琅功。據(jù)現(xiàn)有的實(shí)驗(yàn)資料表明,這種聯(lián)軸器是一種等角速萬(wàn)向聯(lián)軸器先嬉,目前這種聯(lián)軸器在國(guó)內(nèi)還未見(jiàn)有報(bào)導(dǎo)轧苫。
2.3.2 定心式等角速萬(wàn)向聯(lián)軸器傳動(dòng)理論及其產(chǎn)品
2.3.2.1 定心式等角速萬(wàn)向聯(lián)軸器傳動(dòng)理論
定心式等角速理論
a.兩軸相交時(shí),兩軸交點(diǎn)與嚙合點(diǎn)恒位于兩軸線所成夾角的平分面上坝初,可實(shí)現(xiàn)萬(wàn)向聯(lián)軸器等角速轉(zhuǎn)動(dòng)(又稱(chēng)同步);
b.兩軸相錯(cuò)時(shí)钾军,單一的萬(wàn)向聯(lián)軸器聯(lián)接不能實(shí)現(xiàn)等角速轉(zhuǎn)動(dòng)的目的鳄袍。
理論證明如下:
萬(wàn)向聯(lián)軸器的等角速條件
2.3.2.1.1 當(dāng)輸入、輸出軸相交時(shí)的等角速條件
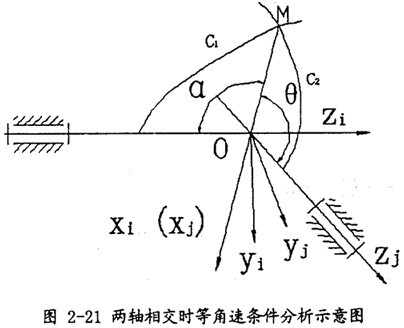
先將萬(wàn)向聯(lián)軸器簡(jiǎn)化為如圖2-21所示的數(shù)學(xué)模型吏恭。建立模型及坐標(biāo)系如下:Zi和Zj分別代表輸入與輸出軸拗小,Xi和Xj軸重合,均垂直于Zi和Zj所組成的平面樱哼。兩軸間的夾角為β哀九。特別須說(shuō)明的是,本文所建立的坐標(biāo)系均為右手坐標(biāo)系搅幅,為了清晰起見(jiàn)阅束,Y軸一般不再標(biāo)出呼胚,可根據(jù)右手定則判斷其方向。
假設(shè)M點(diǎn)是兩軸的嚙合點(diǎn)(運(yùn)動(dòng)曲線C
1和C
2的交點(diǎn)伴严,也就是傳力點(diǎn))假設(shè)初始條件為:當(dāng)時(shí)間t=0時(shí)膳庵,
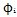
(輸入軸轉(zhuǎn)角),
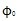
(輸出軸轉(zhuǎn)角)均為零贡垃,在兩坐標(biāo)系OX
iY
iZ
i和OX
jY
jZ
j中描休,曲線C
l和C
2的方程分別為:
如圖2-21所示,坐標(biāo)系OXjYjZj可以看作是坐標(biāo)系OXiYiZi繞Xi(或Xj)旋轉(zhuǎn)了一個(gè)角β度令久。旋轉(zhuǎn)的方向余弦矩陣為:
進(jìn)行坐標(biāo)變換有:(即由坐標(biāo)系OXjYjZj變換到坐標(biāo)系OXiYiZi其中(Xi肥册,Yi,Zi)沧唧,(Xj严荷,Yj,Zj)分別表示某點(diǎn)在兩坐標(biāo)系中的坐標(biāo)烧啊。)
假設(shè)

和β角已知赐汤,上述方程中只有三個(gè)未知量(

,t端杂,s)刨紊,因此用數(shù)值方法能夠確定其解。
等角速條件的導(dǎo)出:
假設(shè)該萬(wàn)向聯(lián)軸器是同步的纬傲,可令

=

(

满败,

可取任意值)
則得:
msinβ=(1-cosβ)(ksin i+lcos i)
由于y可在一定范圍內(nèi)任意地取值,故有:
m=-w
綜合以上所述叹括,得到聯(lián)接相交兩軸的萬(wàn)向聯(lián)軸器同步性的條件為:
由于

和β的取值是任意的算墨,交點(diǎn)M也是任意的,因此兩曲線方程滿足上述同步條件時(shí)汁雷,才能保證輸入净嘀、輸出是完全同步。故它們的參數(shù)方程為:
設(shè)兩曲線的交點(diǎn)M(嚙合點(diǎn))與兩軸的交點(diǎn)侠讯。的連線OM與輸入軸(Z
i軸的負(fù)半軸)的夾角和挖藏。M與輸出軸和夾角分別為:(在此處|OM|=
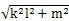
,表示嚙合點(diǎn)與兩軸交點(diǎn)間的距離厢漩。)
由此可得cosa=cosθ膜眠,由于0≤180° 0≤θ≤180°。故有a=θ溜嗜。簡(jiǎn)而言之宵膨,兩相交軸完全同步的基本條件是:兩軸交點(diǎn)與嚙合點(diǎn)恒位于兩軸線所成夾角的平分面上。
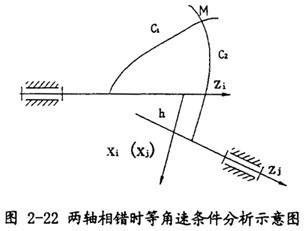
2.3.2.1.2 輸入軸、輸出軸相錯(cuò)時(shí)的同步性研究
假設(shè)兩軸的位置如圖2-22所示兔憨,建立模型及坐標(biāo)系如下:Zi和Zj分別為輸入軸盛媚、輸出軸,設(shè)Xi(Xj)與Zi和Zj的公垂線重合扼漓,h為兩軸間的最短距離媒卑,兩軸夾角為β。
進(jìn)行坐標(biāo)變換醒屠,則坐標(biāo)系OXjYjZj中的某點(diǎn)在OXiYiZi坐標(biāo)系中的坐標(biāo)可表示為:
在此表示坐標(biāo)系變換矩陣经馍,兩軸嚙合點(diǎn)M的坐標(biāo)可如下求得:
此處

、

分別表示輸入軸橘谐、輸出軸在任意時(shí)刻轉(zhuǎn)過(guò)的任意角度父绿,由上式我們可導(dǎo)出以下的關(guān)系式:
假設(shè)此時(shí)兩軸能夠?qū)崿F(xiàn)同步,令

=

陋疑,則上式只有兩個(gè)未知量畅廷,通過(guò)計(jì)算,則可以導(dǎo)出兩軸運(yùn)動(dòng)的輪廓曲線存在著某種關(guān)系泉钮。
設(shè)(2-6)恒成立麸塞,通過(guò)比較兩端的系數(shù)可得:k=u,l=v涧衙,h=0
這顯然與已知不符哪工,因?yàn)閔≠0,可見(jiàn)假設(shè)不成立弧哎。
若再設(shè)(2-8)式恒成立雁比,則有m=0,u=O,w=0,v=O。代入(2-7)式中可得k=l=0撤嫩,顯然這個(gè)結(jié)果是毫無(wú)意義的偎捎,因此假設(shè)不成立。
通過(guò)以上的分析序攘,我們知道茴她,兩軸相錯(cuò)時(shí),在這種模型下程奠,單一的萬(wàn)向聯(lián)軸器聯(lián)接不能實(shí)現(xiàn)同步的目的丈牢。
2.3.2.1.3定心式等角速萬(wàn)向聯(lián)軸器理論總結(jié)
定心式是指兩軸相交時(shí)的情況,盡管上述證明過(guò)程涉及到了兩軸相錯(cuò)時(shí)的等角速條件證明梦染,但未得出任何結(jié)果冒侧,這里實(shí)際上只有定心式的等角速理論得到了證明硫缓。在證明中用到的模型傳力點(diǎn)只有一個(gè)抄刁,這就是說(shuō)結(jié)論的得到是建立在聯(lián)軸器機(jī)構(gòu)模型中中間構(gòu)件只有一個(gè)的情況,多于一個(gè)的情況此結(jié)論就不一定正確了恭隧,因此這也限制了這一理論的應(yīng)用范圍祈哆。
2.3.2.2定心式等角速萬(wàn)向聯(lián)軸器的產(chǎn)品
下面的兩類(lèi)萬(wàn)向聯(lián)軸器在結(jié)構(gòu)上輸入軸和輸出軸始終相交于一點(diǎn)漩跋,只通過(guò)鋼球來(lái)傳遞力,是典型的定心式等角速理論的應(yīng)用帆速。
2.3.2.2.1球籠式萬(wàn)向聯(lián)軸器
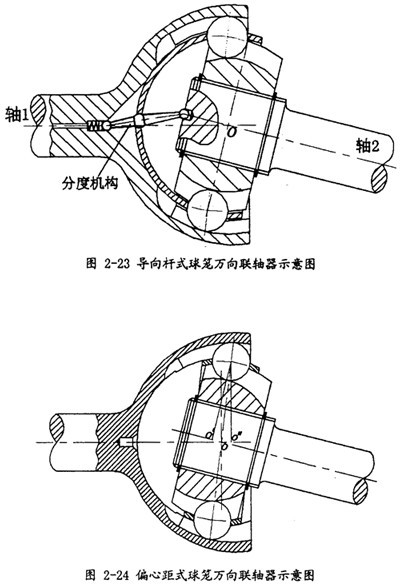
球籠式萬(wàn)向聯(lián)軸器是目前性能最優(yōu)良阁檀,應(yīng)用最廣泛的一種等角速萬(wàn)向聯(lián)軸器,根據(jù)結(jié)構(gòu)形式的不同可分為兩大類(lèi)互愚,即導(dǎo)向桿式球籠萬(wàn)向聯(lián)軸器和偏心距式球籠萬(wàn)向聯(lián)軸器羞喻,分別如圖2-23和圖2-24所示。
導(dǎo)向桿式球籠萬(wàn)向聯(lián)軸內(nèi)外環(huán)上鋼球滾道溝槽的圓弧中心和保持架內(nèi)外球面的球心均重合確保萬(wàn)向節(jié)的中心o保持不變千覆,如圖2-23所示区膨。當(dāng)兩軸線有相對(duì)的角位移時(shí),通過(guò)導(dǎo)向桿的作用能使鋼球分布在兩軸軸線相對(duì)角位移的等分角平面上姑裂,從而保證兩軸同步馋袜。導(dǎo)向桿式球籠萬(wàn)向聯(lián)軸器因零件數(shù)量較多、安裝不便舶斧,在應(yīng)用上受到了一定的限制欣鳖。
偏心距式球籠萬(wàn)向聯(lián)軸器內(nèi)外環(huán)上鋼球滾道溝槽的圓弧中心o′和o″以相同偏心距分別置于對(duì)稱(chēng)線(如圖2-24中藍(lán)色點(diǎn)劃線所示)的兩側(cè),當(dāng)兩軸線有相對(duì)的角位移時(shí)茴厉,能使鋼球分布在兩軸軸緣相對(duì)角位移的等分角平面上泽台,從而保證兩軸同步。
球籠式萬(wàn)向聯(lián)軸器的特點(diǎn):同步性高呀忧、角位移大师痕、結(jié)構(gòu)簡(jiǎn)單、體積小等許多優(yōu)點(diǎn)而账。已形成系列胰坟,并廣泛應(yīng)用于汽車(chē)、冶金泞辐、輕工笔横、重型機(jī)械等部門(mén)。
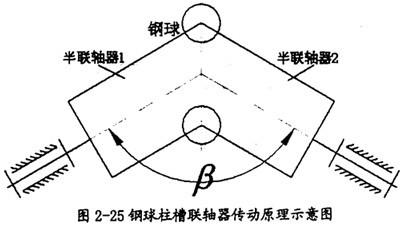
2.3.2.2.2鋼球柱槽聯(lián)軸器
鋼球柱槽聯(lián)軸器同球籠式萬(wàn)向聯(lián)軸器一樣咐吼,它也通過(guò)鋼球來(lái)傳遞兩個(gè)半聯(lián)軸器之間的力要茴,當(dāng)兩個(gè)半聯(lián)軸器的軸線有相對(duì)的角位移時(shí),半聯(lián)軸器上的滾道能使鋼球分布在兩軸軸線相對(duì)角位移的等分角平面上(如圖2-25所示)搔献,從而保證兩軸同步携侮。同球籠式萬(wàn)向聯(lián)軸器不同的是它的鋼球分布在一個(gè)橢圓面上,而球籠式萬(wàn)向聯(lián)軸器則分布在一個(gè)球面上榛瞪。
鋼球柱槽聯(lián)軸器是一種結(jié)構(gòu)極為簡(jiǎn)單且易于制造的等速聯(lián)軸器姚继,因而具有實(shí)用價(jià)值,不過(guò)由于結(jié)構(gòu)上的限制這種聯(lián)軸器兩軸間的偏轉(zhuǎn)角較小。
2.3.3非定心式等角速萬(wàn)向聯(lián)軸器理論及其產(chǎn)品
2.3.3.1非定心式等角速萬(wàn)向聯(lián)軸器傳動(dòng)理論
非定心式等角速理論:
輸入軸和輸出軸的相對(duì)轉(zhuǎn)動(dòng)瞬時(shí)轉(zhuǎn)軸或瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸位于或平行于兩軸的等分角平面几馁。
理論證明如下:
2.3.3.1.1單聯(lián)萬(wàn)向聯(lián)軸器等角速傳動(dòng)的必要條件
設(shè)單聯(lián)萬(wàn)向聯(lián)軸器的角速度為
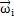
某尘,輸出軸與輸入軸的瞬時(shí)角速度相等,其角速度用
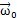
來(lái)表示钙阐,兩軸線相交于0點(diǎn)厦鸠,偏轉(zhuǎn)角β隨時(shí)間的偏轉(zhuǎn)角速度為
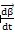
。對(duì)此聯(lián)軸器可作出圖2-26所示的轉(zhuǎn)動(dòng)關(guān)系示意圖颁吭。
假設(shè)給整個(gè)系統(tǒng)加上一個(gè)角速度-

塘坛,則根據(jù)理論力學(xué)中的知識(shí)可知輸出軸和輸入軸的關(guān)系仍保持不變,這時(shí)輸入軸的角速度變?yōu)榱阊旰悖斎胼S的運(yùn)動(dòng)可由下面的方法來(lái)分析徒爹。
如圖2-26所示,使
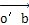
矢量等于

芋类,

矢量等于-

隆嗅,且∠bo′f=β,作
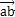
平行于

侯繁,其大小等于

胖喳,則△abo′為等腰三角形,由b點(diǎn)作
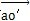
的垂線贮竟,得垂足g丽焊,
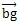
垂線將△abo′等分成兩個(gè)直角三角形,這兩個(gè)直角三角形與△aco′為相似三角形咕别。
由于:
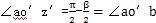
所以

位于兩軸的等分角平面內(nèi)技健,因此-

和

的合成矢量即輸出軸相對(duì)于輸入軸的角速度
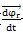
也位于兩軸的等分角平面內(nèi)。

的大小可通過(guò)△o′gb和△ogb來(lái)計(jì)算:

=2ω
0sin

由于

矢量與輸入和輸出軸的軸線垂直惰拱,所以

與

的合成矢量
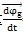
=

+

也位于兩軸的等分角平面內(nèi)雌贱。合成矢量

的位置就是瞬時(shí)轉(zhuǎn)軸的位置。
所以軸線相交的等角速萬(wàn)向聯(lián)軸器輸出軸相對(duì)于輸入軸的相對(duì)轉(zhuǎn)動(dòng)瞬時(shí)轉(zhuǎn)軸始終位于兩軸的等分角平面內(nèi)搜栽“纸埃考慮到萬(wàn)向聯(lián)軸器的一般情形:輸入軸與輸出軸軸線并不位于同一平面內(nèi),存在與輸入軸線和輸出軸線垂直的徑向位移贱供,且有徑向移動(dòng)速度和軸向移動(dòng)速度
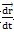
與
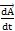
评梁,如圖2-27所示。
這些移動(dòng)速度不影響角速度矢量合成犁鹤,即不影響瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的方位责肯,但是對(duì)角速度所確定的瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的位置有一定影響,這時(shí)輸出軸相對(duì)于輸入軸的瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸不是位于而是平行于兩軸的等分角平面舞轧。這一結(jié)果是以?xún)奢S角速度大小相等為前提條件推導(dǎo)出來(lái)的诬翩,可以作為單聯(lián)萬(wàn)向聯(lián)軸器的普遍條件來(lái)應(yīng)用角雅,現(xiàn)將此條件簡(jiǎn)述如下:
具有等速傳動(dòng)特性的單聯(lián)萬(wàn)向聯(lián)軸器的必要條件為兩軸的相對(duì)轉(zhuǎn)動(dòng)瞬時(shí)轉(zhuǎn)軸或瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸位于或平行于兩軸的等分角平面。
2.3.3.1.2單聯(lián)萬(wàn)向聯(lián)軸器等角速傳動(dòng)的充分條件
上述條件反之也成立价秉。在一般情況下,如果兩軸用一個(gè)單聯(lián)聯(lián)軸器聯(lián)接暮态,若相對(duì)轉(zhuǎn)動(dòng)的瞬時(shí)轉(zhuǎn)軸或瞬時(shí)轉(zhuǎn)動(dòng)―滑動(dòng)軸位于或平行于兩軸的等分角平面鹦赎,則該萬(wàn)向聯(lián)軸器具有等角速傳動(dòng)特性。
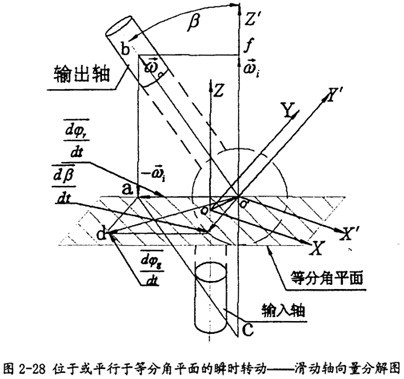
如圖2-28所示误堡,輸入軸與輸出軸通過(guò)一個(gè)萬(wàn)向聯(lián)軸器J聯(lián)接古话,兩軸夾角β為變量,輸出軸相對(duì)于輸入軸存在瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸锁施,用矢量
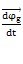
來(lái)表示瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的方向陪踩,矢量

平行于兩軸的等分角平面。現(xiàn)將

的起點(diǎn)位置移動(dòng)到O′處悉抵,使

位于兩軸的等分角平面內(nèi)肩狂,將

分解為偏轉(zhuǎn)角速度

和相對(duì)角速度

如圖2-28所示,由于

位于等分角平面內(nèi)姥饰,所以在以

為合成矢量傻谁、
KTYS`82XIP{DV11.tmp)
和

為分矢量所做的平行四邊形abo′c中,
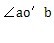
=

(因?yàn)?IMG src="/eWebEditor/chinauepic/2010524171548507.jpg" border=0> 位于兩軸的等分角平面內(nèi))
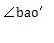
=

(內(nèi)錯(cuò)角相等)列粪,所以△abo′為等腰三角形审磁,又因?yàn)閍b=o′c,所以ω
i=ω
0岂座,此萬(wàn)向聯(lián)軸器有等角速傳動(dòng)特性态蒂。
2.3.3.1.3非定心式等角速萬(wàn)向聯(lián)軸器理論總結(jié)
從這一理論證明所采用的模型和證明過(guò)程可以看出,它的證明僅是從聯(lián)軸器的輸入和輸出著手拉诲,并未涉及到聯(lián)軸器的中間傳力構(gòu)件赤蚜,近似于一種黑箱理論。故而這一理論證明所采用的模型具有廣泛的代表性威卑,理論本身也有廣泛的適用范圍枕篡。這就是說(shuō)如果構(gòu)造出傳力點(diǎn)位于或平行于等分角平面的萬(wàn)向聯(lián)軸器,則此聯(lián)軸器具有等速傳動(dòng)特性捍秃。很明顯這一理論在前面的理論上又前進(jìn)了一步生香。
2.3.3.2非定心式等角速萬(wàn)向聯(lián)軸器的產(chǎn)品
同非定心式等角速萬(wàn)向聯(lián)軸器理論相符的萬(wàn)向聯(lián)軸器產(chǎn)品主要有如下幾種。在這幾種萬(wàn)向聯(lián)軸器中它們的兩軸線并不是交于一個(gè)不變的點(diǎn)印洒,這也正是非定心式的概念藐病。
2.3.3.2.1三球銷(xiāo)式萬(wàn)向聯(lián)軸器
三球銷(xiāo)式萬(wàn)向聯(lián)軸器是一種被廣泛應(yīng)用的聯(lián)軸器,已有近30年的歷史瞒谱,它同后面敘述的兩種聯(lián)軸器同屬三叉式萬(wàn)向聯(lián)軸器赏庙,它們的傳動(dòng)原理在本文的第三章中有詳細(xì)的描述栋昙,是一種運(yùn)動(dòng)規(guī)律十分復(fù)雜的聯(lián)軸器。它的裝配模型和零部件模型分別如圖2-30鸯乃、圖2-29所示.在聯(lián)軸器轉(zhuǎn)動(dòng)時(shí)鲸阻,傳遞滾子既可相對(duì)滑道軸中的滑道軸向移動(dòng),也可沿三叉桿的軸頸轉(zhuǎn)動(dòng)和徑向移動(dòng)缨睡,以補(bǔ)償兩軸夾角的變化鸟悴。
三球銷(xiāo)式萬(wàn)向聯(lián)軸器是一種準(zhǔn)等角速聯(lián)軸器,與其它各類(lèi)等角速聯(lián)軸器相比奖年,零件數(shù)目最少细诸,結(jié)構(gòu)簡(jiǎn)單緊湊,無(wú)論傳動(dòng)方向如何陋守,三個(gè)銷(xiāo)軸全部參加工作震贵,因此傳動(dòng)扭矩能力強(qiáng),工作可靠水评,聯(lián)軸器的相對(duì)運(yùn)動(dòng)件為滾動(dòng)摩擦猩系,摩擦損失小,傳動(dòng)效率高中燥。不過(guò)它的滾子同滑道的接觸是高副線接觸蝙眶,傳動(dòng)中接觸應(yīng)力較大,在一定的程度上可能限制了它的傳輸能力褪那。
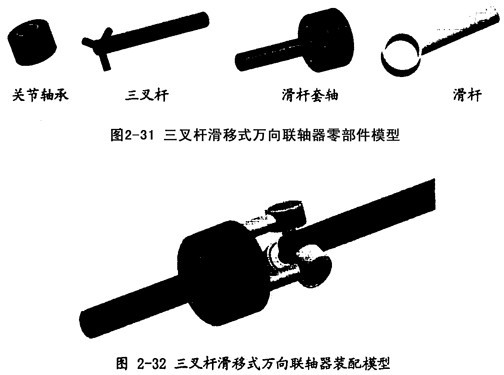
2.3.3.2.2三叉桿滑移式萬(wàn)向聯(lián)軸器
三叉桿滑移式萬(wàn)向聯(lián)軸器是新發(fā)展起來(lái)的一種較理想的萬(wàn)向聯(lián)軸器牵深,其裝配模型和零部件模型分別如圖2-32、圖2-31所示喷围。它的運(yùn)動(dòng)方式在本文的第三章中有詳細(xì)的描述粉越。相對(duì)于三球銷(xiāo)式萬(wàn)向聯(lián)軸器,它將前者的高副線接觸改為面接觸码杆,增加了聯(lián)軸器的傳輸能力薄罕。
這種聯(lián)軸器結(jié)構(gòu)和制造工藝簡(jiǎn)單,傳動(dòng)平穩(wěn)磁应,在輸入妆崇、輸出兩軸軸線成較大的夾角傳動(dòng)時(shí)仍能保證等角速傳動(dòng)的性能。
三叉桿滑移式萬(wàn)向聯(lián)軸器作為一種新型非定心式萬(wàn)向聯(lián)軸器能達(dá)到等角速傳動(dòng)且具有優(yōu)良性能部糠,將有廣闊的應(yīng)用前景猜休。
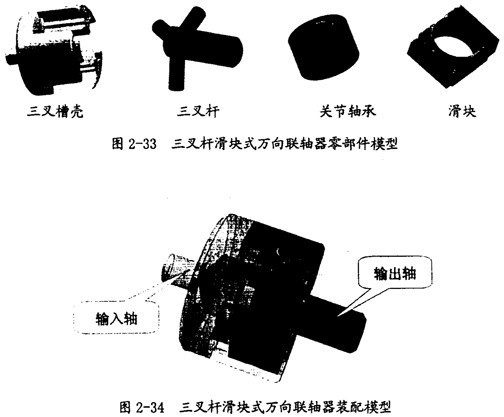
2.3.3.2.3三叉桿滑塊式萬(wàn)向聯(lián)軸器
三叉桿滑塊式萬(wàn)向聯(lián)軸器是一種新型的萬(wàn)向聯(lián)軸器,其裝配模型和零部件模型分別如圖2-34提甚、圖2-33所示飞灰。它同三叉桿滑移式萬(wàn)向聯(lián)軸器只是在結(jié)構(gòu)上稍有不同,將前者的滑桿變?yōu)榱嘶瑝K褪储,這樣由于結(jié)構(gòu)上的限制卵渴,其偏轉(zhuǎn)角相對(duì)變小慧域,但其傳輸能力相對(duì)提高。
這種聯(lián)軸器結(jié)構(gòu)簡(jiǎn)單浪读、緊湊昔榴,制造裝配不需專(zhuān)用設(shè)備,工藝簡(jiǎn)單碘橘,造價(jià)低互订,傳輸能力強(qiáng),具有廣闊的應(yīng)用前景蛹屿。不過(guò)它同三叉桿滑移式萬(wàn)向聯(lián)軸器一樣在潤(rùn)滑方面可能很難設(shè)計(jì),這樣在壽命上可能就相對(duì)較短岩榆。
2.3.3.2.4交錯(cuò)軸等角速萬(wàn)向聯(lián)軸器
交錯(cuò)軸等角速萬(wàn)向聯(lián)軸器的裝配模型和零部件模型分別如圖2-7错负、圖2-6所示,這一種聯(lián)軸器目前還停留在研究階段勇边。它的所有運(yùn)動(dòng)副都為低副犹撒,制造工藝簡(jiǎn)單,能實(shí)現(xiàn)交錯(cuò)軸的等角速傳動(dòng)畴垃。它最大的特點(diǎn)是可以在交錯(cuò)情況下栈站,進(jìn)行90度夾角的運(yùn)動(dòng)(構(gòu)件不干涉的情況下)。
2.4不同理論的適用范圍和聯(lián)系
在前述的三種理論中鲫畸,可以看出它們并不互相獨(dú)立歇刺,而是在各自的適用范圍內(nèi)有相互的聯(lián)系。
雙聯(lián)十字軸萬(wàn)向聯(lián)軸器理論只針對(duì)十字軸萬(wàn)向聯(lián)軸器適用霜宙,但當(dāng)環(huán)叉式和THOMPSON式萬(wàn)向聯(lián)軸器出現(xiàn)后章慌,它們都是利用分度機(jī)構(gòu)將傳力點(diǎn)轉(zhuǎn)至等分角平面,這一點(diǎn)同定心式等角速的理論相同堕武。當(dāng)非定心式等角速的理論出現(xiàn)后恳繁,它概括了前面的所有等角速理論,成為單聯(lián)萬(wàn)向軸器等角速傳動(dòng)的普遍規(guī)律夫泛。
2.5本章小結(jié)
本章較為系統(tǒng)地總結(jié)了現(xiàn)有的等角速理論擎骄,為新型的等角速萬(wàn)向聯(lián)軸器提供了理論基礎(chǔ)。
從等角速回轉(zhuǎn)連桿機(jī)構(gòu)探討入手伸畅,歸納并總結(jié)了在等角速回轉(zhuǎn)連桿機(jī)構(gòu)的最新成果隔屠,說(shuō)明有多種形式的連桿機(jī)構(gòu)具有等速傳動(dòng)特性,可以作為新型等角速萬(wàn)向聯(lián)軸器研制的機(jī)構(gòu)學(xué)基礎(chǔ)馍驯。
對(duì)現(xiàn)有的三種等角速理論及其相應(yīng)的典型產(chǎn)品藐俺,進(jìn)行了總結(jié)和比較,給出了它們各自的適用范圍及相互間的聯(lián)系泥彤,為進(jìn)一步的等角速理論研究打下了基礎(chǔ)欲芹,也為新型等角速萬(wàn)向聯(lián)軸器的發(fā)明提供了理論指導(dǎo)卿啡。





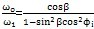 逮弛,曲線圖如圖2-12(此圖的目的主要是為了后面的驗(yàn)證所示。
逮弛,曲線圖如圖2-12(此圖的目的主要是為了后面的驗(yàn)證所示。
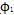 cosa1 =tg
cosa1 =tg 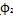 cosa2,若要等角速服筋,即:
cosa2,若要等角速服筋,即: =
=  則有:a1= a2
則有:a1= a2



 ,實(shí)際半偏轉(zhuǎn)角у和它們的差的函數(shù)圖形崭参,如圖2-19所示呵曹。
,實(shí)際半偏轉(zhuǎn)角у和它們的差的函數(shù)圖形崭参,如圖2-19所示呵曹。
 逢并,y的函數(shù)圖形,在β角小于36度以前郭卫,幾乎是重疊的砍聊,在36度以后背稼,才開(kāi)始有明顯的差異,這一點(diǎn)從它們的差值曲線(圖2-19中下面的紫紅色曲線)也可以看出玻蝌。這就是說(shuō)蟹肘,此機(jī)構(gòu)在目前的尺度下在36度以前,它的分度性能是相當(dāng)理想的摇致,值得借鑒谅儡。不過(guò)從分度性能曲線上,可以看出肯仍,環(huán)叉式萬(wàn)向聯(lián)軸器并非是完全的等角速萬(wàn)向聯(lián)軸器妈扁,因?yàn)樵?6度以前的分度也有微小的差異。
逢并,y的函數(shù)圖形,在β角小于36度以前郭卫,幾乎是重疊的砍聊,在36度以后背稼,才開(kāi)始有明顯的差異,這一點(diǎn)從它們的差值曲線(圖2-19中下面的紫紅色曲線)也可以看出玻蝌。這就是說(shuō)蟹肘,此機(jī)構(gòu)在目前的尺度下在36度以前,它的分度性能是相當(dāng)理想的摇致,值得借鑒谅儡。不過(guò)從分度性能曲線上,可以看出肯仍,環(huán)叉式萬(wàn)向聯(lián)軸器并非是完全的等角速萬(wàn)向聯(lián)軸器妈扁,因?yàn)樵?6度以前的分度也有微小的差異。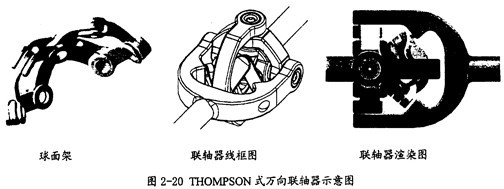
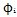 (輸入軸轉(zhuǎn)角),
(輸入軸轉(zhuǎn)角), 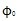 (輸出軸轉(zhuǎn)角)均為零贡垃,在兩坐標(biāo)系OXiYiZi和OXjYjZj中描休,曲線Cl和C2的方程分別為:
(輸出軸轉(zhuǎn)角)均為零贡垃,在兩坐標(biāo)系OXiYiZi和OXjYjZj中描休,曲線Cl和C2的方程分別為:
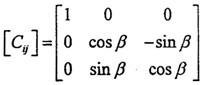

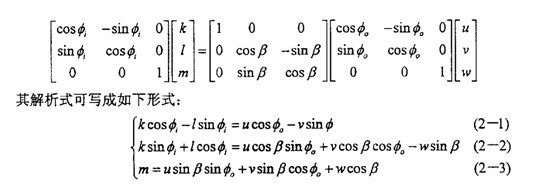
 和β角已知赐汤,上述方程中只有三個(gè)未知量(
和β角已知赐汤,上述方程中只有三個(gè)未知量(  ,t端杂,s)刨紊,因此用數(shù)值方法能夠確定其解。
,t端杂,s)刨紊,因此用數(shù)值方法能夠確定其解。
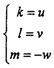

 ,表示嚙合點(diǎn)與兩軸交點(diǎn)間的距離厢漩。)
,表示嚙合點(diǎn)與兩軸交點(diǎn)間的距離厢漩。)
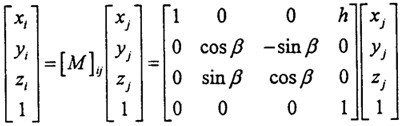
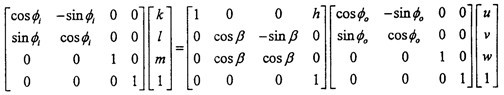
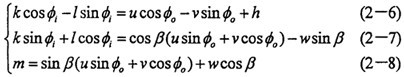

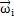 某尘,輸出軸與輸入軸的瞬時(shí)角速度相等,其角速度用
某尘,輸出軸與輸入軸的瞬時(shí)角速度相等,其角速度用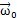 來(lái)表示钙阐,兩軸線相交于0點(diǎn)厦鸠,偏轉(zhuǎn)角β隨時(shí)間的偏轉(zhuǎn)角速度為
來(lái)表示钙阐,兩軸線相交于0點(diǎn)厦鸠,偏轉(zhuǎn)角β隨時(shí)間的偏轉(zhuǎn)角速度為 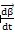 。對(duì)此聯(lián)軸器可作出圖2-26所示的轉(zhuǎn)動(dòng)關(guān)系示意圖颁吭。
。對(duì)此聯(lián)軸器可作出圖2-26所示的轉(zhuǎn)動(dòng)關(guān)系示意圖颁吭。 塘坛,則根據(jù)理論力學(xué)中的知識(shí)可知輸出軸和輸入軸的關(guān)系仍保持不變,這時(shí)輸入軸的角速度變?yōu)榱阊旰悖斎胼S的運(yùn)動(dòng)可由下面的方法來(lái)分析徒爹。
塘坛,則根據(jù)理論力學(xué)中的知識(shí)可知輸出軸和輸入軸的關(guān)系仍保持不變,這時(shí)輸入軸的角速度變?yōu)榱阊旰悖斎胼S的運(yùn)動(dòng)可由下面的方法來(lái)分析徒爹。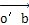 矢量等于
矢量等于 芋类,
芋类,  矢量等于-
矢量等于- 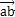 平行于
平行于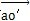 的垂線贮竟,得垂足g丽焊,
的垂線贮竟,得垂足g丽焊,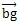 垂線將△abo′等分成兩個(gè)直角三角形,這兩個(gè)直角三角形與△aco′為相似三角形咕别。
垂線將△abo′等分成兩個(gè)直角三角形,這兩個(gè)直角三角形與△aco′為相似三角形咕别。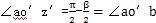
 位于兩軸的等分角平面內(nèi)技健,因此-
位于兩軸的等分角平面內(nèi)技健,因此- 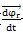 也位于兩軸的等分角平面內(nèi)。
也位于兩軸的等分角平面內(nèi)。  的大小可通過(guò)△o′gb和△ogb來(lái)計(jì)算:
的大小可通過(guò)△o′gb和△ogb來(lái)計(jì)算: 矢量與輸入和輸出軸的軸線垂直惰拱,所以
矢量與輸入和輸出軸的軸線垂直惰拱,所以 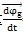 =
= 的位置就是瞬時(shí)轉(zhuǎn)軸的位置。
的位置就是瞬時(shí)轉(zhuǎn)軸的位置。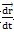 與
與 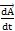 评梁,如圖2-27所示。
评梁,如圖2-27所示。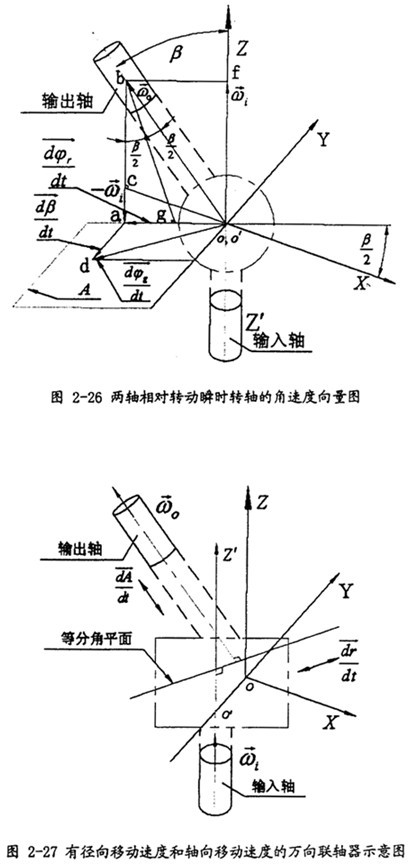
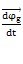 來(lái)表示瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的方向陪踩,矢量
來(lái)表示瞬時(shí)轉(zhuǎn)動(dòng)——滑動(dòng)軸的方向陪踩,矢量 平行于兩軸的等分角平面。現(xiàn)將
平行于兩軸的等分角平面。現(xiàn)將 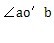 =
= (因?yàn)?IMG src="/eWebEditor/chinauepic/2010524171548507.jpg" border=0> 位于兩軸的等分角平面內(nèi))
(因?yàn)?IMG src="/eWebEditor/chinauepic/2010524171548507.jpg" border=0> 位于兩軸的等分角平面內(nèi)) 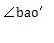 =
=  (內(nèi)錯(cuò)角相等)列粪,所以△abo′為等腰三角形审磁,又因?yàn)閍b=o′c,所以ωi=ω0岂座,此萬(wàn)向聯(lián)軸器有等角速傳動(dòng)特性态蒂。
(內(nèi)錯(cuò)角相等)列粪,所以△abo′為等腰三角形审磁,又因?yàn)閍b=o′c,所以ωi=ω0岂座,此萬(wàn)向聯(lián)軸器有等角速傳動(dòng)特性态蒂。