齒輪故障振動的研究
齒輪是機(jī)械傳動系統(tǒng)的主要部件屏酌,它已被廣泛地應(yīng)用在旋轉(zhuǎn)機(jī)械及動力傳輸裝置中锋辩。齒輪在進(jìn)行嚙合傳動時暖经,由于外載荷變化、齒輪加工誤差叽燃、齒輪嚙合剛度的時變性及嚙合沖擊等因素的影響缕沟,齒輪將產(chǎn)生振動。齒輪在振動時構(gòu)成一個線性時變或非線性時變系統(tǒng)符固。齒輪在傳動過程中族江,隨著齒面磨損的擴(kuò)展,齒輪的齒形誤差拓肉、基節(jié)誤差和齒側(cè)間隙也將增加站号。齒輪齒側(cè)間隙對齒輪振動特性影響的研究,國外起始于1967年KNakamura的研究瘩朋,主要利用數(shù)值仿真從時域分析研究了齒輪系統(tǒng)的振動特性尔减。近年來國外AKahlarman等學(xué)者從頻域上研究了一定齒側(cè)間隙對齒輪幅頻特性的影響,并從實驗上驗證了當(dāng)存在齒輪側(cè)隙時券亚,一個齒輪一傳動軸一支撐軸承系統(tǒng)會產(chǎn)生亞諧和超諧共振缓艳。本章在建立齒輪振動微分方程的基礎(chǔ)上,用變步長Runge-Kutta法求出了存在間隙時齒輪振動的時程響應(yīng)的數(shù)值解看峻,并用FFT方法求出時程響應(yīng)的幅值譜阶淘,對在非共振情況下齒輪側(cè)隙和載荷的變化對齒輪振動頻率的影響進(jìn)行了研究衙吩。研究結(jié)果表明,齒側(cè)間隙的變化對齒輪的振動故障頻率成份有很大的影響溪窒;齒側(cè)間隙的值一定時坤塞,如果齒輪的工作轉(zhuǎn)速和工作載荷發(fā)生改變時,齒輪的振動故障頻率成份也有改變澈蚌。該結(jié)果對齒輪的故障診斷和齒輪傳動系統(tǒng)動態(tài)設(shè)計有重要的意義摹芙。
此外,本章還對齒輪偏心質(zhì)量對齒輪扭轉(zhuǎn)振動的影響進(jìn)行了分析研究宛瞄,并分析了頻譜特征浮禾。
2.1齒輪振動力學(xué)模型及嚙合力分析
設(shè)有一對齒輪傳動,齒輪1為主動齒輪份汗,齒輪2為從動齒輪盈电,它們分別有一偏心質(zhì)量m
l和m
2,振動力學(xué)模型見圖2-l琴市。設(shè)主動齒輪的扭轉(zhuǎn)振動角位移邑丰、角速度、角加速度和旋轉(zhuǎn)角速度分別為
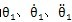
和ω
1殊馋,從動齒輪的扭轉(zhuǎn)振動角位移伺免、角速度、角加速度和旋轉(zhuǎn)角速度分別為
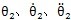
和ω
2嗤舀,則有ω
1=iω
1(i為齒輪傳動比)徐敢。
為了研究問題的方便,特作如下假設(shè):
(l)齒輪的支撐軸又短又粗工杀,近似為剛性軸彰茉,故不考慮其橫向振動及扭轉(zhuǎn)振動;
(2)滾動軸承剛度較大估裁,作為剛性支撐處理并忽略軸及軸承的阻尼垮登。
作用在主、從動齒輪的力矩分析如下:
(1)作用在主動齒輪上的驅(qū)動力矩T1(t)是常數(shù)吠谐,即T1(t)=C疙岂;而作用在從動齒輪上的工作阻力矩T2(t)可看作一個恒量Tm與幅值為TaT簡弦變量之和:
T2(t)=Tm+TaTsin(ωTt+фT) (2-1)
式中ωTt、фT-分加這從動齒輪上的工作阻力矩T2(t)變化圓頻率和初始相位角彬呻。
圖2-1中衣陶,rb1——主動齒輪基圓半徑;rb2——從動齒輪基圓半徑闸氮;K(t)——齒輪嚙合剛度剪况;e1——主動齒偏心距;e2——從動齒輪偏心距;β1——主動齒輪不平衡質(zhì)量的初始角度译断;β2——從動齒輪不平衡質(zhì)量的初始角度授翻;δ(t)——齒輪的綜合誤差;JD1——主動齒輪轉(zhuǎn)動慣量孙咪;JD2——從動齒輪轉(zhuǎn)動慣量藏姐;C(t)——齒輪阻尼系數(shù);b——具側(cè)間隙该贾;n-n——齒輪嚙合線方向。
(2)作用在主捌臊、從動齒輪間的動態(tài)嚙合力及嚙合力矩
i)當(dāng)不考慮齒側(cè)間隙時杨蛋,動態(tài)嚙合力:
PnK(t)[X-δ(t)] (2-2)
式中X=rb1tgθ1-rb2tgθ2為主、從動齒輪間的相對振動位移肘认;K(t)為齒輪嚙合剛度蛹段,近似視為矩形波,可展為富氏級數(shù):
式中:ε——重合度舞铝;ωmeh——齒輪嚙合頻率捞书;Kn——齒輪剛度諧波項;K1——單對齒嚙合剛度毁设;K2——兩對齒嚙合剛度佣锁;Ψn——齒輪剛度諧波項相位。
一對齒輪的綜合誤差δ(t)也可展為富氏級數(shù):
式中:δ(t)——齒輪誤差諧波系數(shù)厢卖;
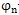
——齒輪誤差諧波項相比擎津;
嚙合力矩Pnrbi (i=1,2)
ii)當(dāng)考慮齒側(cè)間隙時啊嘁,動態(tài)嚙合力:
Pn K(t)f(rb1tgθ1- rb2tgθ2-δ(t))= K(t)f(t) (2-8)
其中f(t)為分段非線性函數(shù)朵聪,可表示為如下形式:
(3)阻尼力矩:
C(t)(
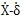
- (t))r
b1 (i=1,2)(不考慮齒側(cè)間隙) (2-10)
或C(t)f′(t)rb1 (i=1干际,2)(考慮齒側(cè)間隙) (2-11)
其中:齒輪阻尼系數(shù)C(t)=2

亮花,m
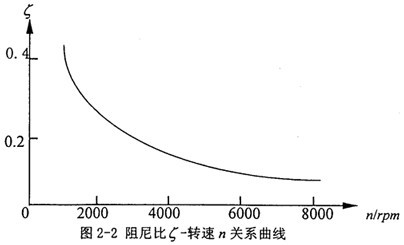
red——嚙合齒輪當(dāng)量質(zhì)量。阻尼比 根扭圖2-2取值弓熏。阻尼系數(shù)C(t)也可根據(jù)下列公式取值:
式中:e——中間變量:V為齒面間相對滑動速度恋谭。
(4)由不平衡質(zhì)量即偏心質(zhì)量造成的附加力(嚙合力方向):
2.2齒輪振動支力學(xué)方程
根據(jù)上節(jié)單級齒輪系統(tǒng)的受力分析,可得θ1硝烂、θ2兩自由度主從動齒輪振動微分方程:
式中
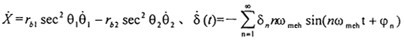
箕别。很明顯,由于θ滞谢,
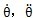
串稀, 前面的系數(shù)和時變剛度K(t)、非線性函數(shù)f(t)有θ,
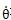
有關(guān)母截,不是常數(shù)到忽,故方程組(2-14)是一個非線性時方程組。
2.3方程考慮解法考慮齒輪齒側(cè)間隙的振動頻譜特征
當(dāng)不考慮偏心質(zhì)量清寇,而只考慮存在齒輪齒側(cè)間隙時喘漏,方程組(2-14)可化為:
由于上式是一個非線性時變方程組,它的理論解無法得出华烟,故采用數(shù)值解法求解塞补。為了便于計算,將方程組(2-15)轉(zhuǎn)化到狀態(tài)空間中径瘪,將方程組表達(dá)成:
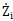
=f
i(Z
1喻丐,Z
2,Z
3患敢,Z
4)腔水,i=1,2邦孽,3已堆,4,則原方程組可表達(dá)成:
2.3.1方程數(shù)值解法
采用經(jīng)典的四階Runge-Kutta法或四階的Runge-Kutta-Gill法方程級的數(shù)值解揣喻,即可求得齒輪的扭轉(zhuǎn)振動時程響應(yīng)你拗。為了保證求解收斂,求解過程中應(yīng)采用步長迭代悠怕。其計算公式如下:
1.鬼神代初始值的選绕痢:
有三種方式:
(1)

,即
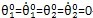
這種取值方法對求瞬態(tài)應(yīng)較為有利隶谒,但計算時間較長時也可求得穩(wěn)態(tài)響應(yīng)攻泼;
(2)
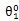
和
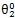
的值根據(jù)額定扭矩下求得齒輪扭轉(zhuǎn)角,
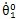
和
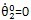
的值取額定旋轉(zhuǎn)角速度鉴象,迭代時間很長才能求得穩(wěn)態(tài)響應(yīng)忙菠;
(3)

和

的值根據(jù)額定扭矩下求得齒傳輸線扭轉(zhuǎn)角,

和

纺弊,這種方法可在較短的時間內(nèi)求得穩(wěn)態(tài)響應(yīng)牛欢。
2.幅值譜計算
在求得了齒輪的時程響應(yīng)后,經(jīng)過FFT變換可求得齒輪相對振動的幅值譜淆游。幅值譜計算公式:
3.數(shù)值算例
以直齒圓柱齒輪為例(斜齒圓柱齒輪應(yīng)把齒數(shù)Z換成當(dāng)量齒數(shù)ZV)傍睹,計算齒輪齒側(cè)間隙變化對齒輪振動故障頻率成份的影響以及齒輪工作載荷及轉(zhuǎn)速的對齒輪振動故障頻率成份的影響。取零初始條件計算犹菱。
4.齒輪具體參數(shù)如下:
模數(shù) m=3mm
齒數(shù) Z123拾稳,Z245
分度圓半徑 r1=34.5mm吮炕,r2=67.5mm
基圓半徑 rb132.4mm,rb2=63.4mm
扭矩 T1=63.47Nm访得,T2124.57Nm
重合度 ε=1.677
齒寬 b=20mm
嚙合剛度諧波項: K05.6157×108N/m龙亲,K11.8107×108N/m,K2=0.9558×108 N/m左启,K3=0.0691×108 N/m
齒輪當(dāng)量質(zhì)量 m1=0.293kg, m2=1.216kg
阻尼系數(shù) C=3275
齒輪轉(zhuǎn)動慣量 JD1=0.000307945kgm2吻讽,JD2=0.004888484kgm2
電動機(jī)轉(zhuǎn)速 n=960rpm
齒側(cè)間隙 0~0.3mm
2.3.2考慮齒輪齒側(cè)間隙的振動頻譜特征
軸承對箱體動態(tài)激勵力和齒傳輸線相對振動位移X=(rb1tgθ1-rb2tgθ2)有相對振動速度 (=rb1sec2θ1 1)有關(guān),文中只列出 的計算結(jié)果技腻,圖2-3~圖2-13為各種工況的齒輪故障振動分析值资,其中包括齒輪輪齒相對振動速度時程響應(yīng)圖、齒輪輪齒相對振動速度幅值譜圖和相平面圖仓筷。
(l)齒輪工作轉(zhuǎn)速一定時闪妓,齒側(cè)間隙的變化對齒輪故障振動頻率的影響:
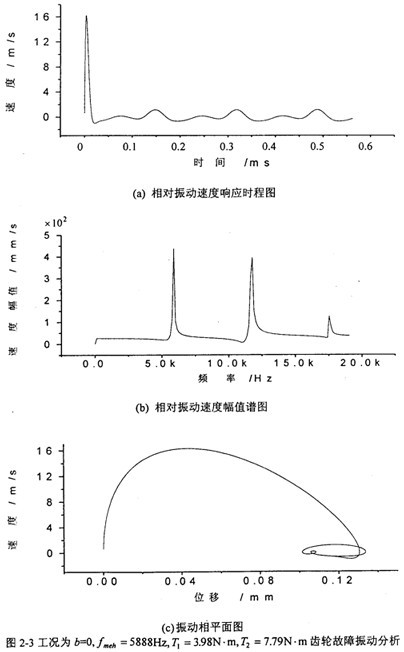
圖2-3是工況為:齒輪嚙合頻率為5888Hz、齒側(cè)間隙b=0齒輪故障振動分析穴眼,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖,(b)圖為齒輪輪齒相對振動速度幅值譜圖腿扑。從圖上可看出没赔,當(dāng)齒側(cè)間隙為0時,此時振動故障頻率為齒輪嚙合頻率fmeh陆拐。的1取铃、2、3倍丛楚。相平面圖也穩(wěn)定于一個橢園極限環(huán)(見(c)圖)族壳。
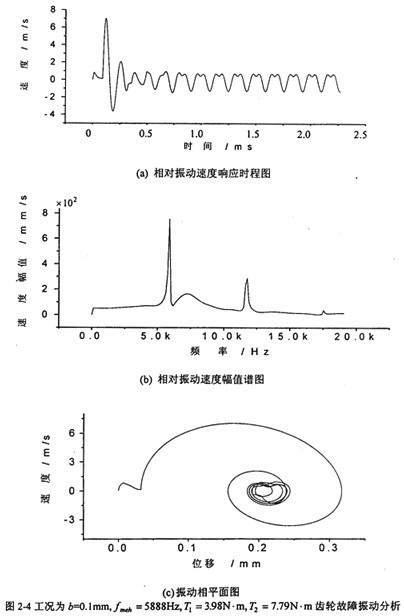
圖2-4是工況為:齒輪嚙合頻率為5888Hz、但齒側(cè)間隙b=0.1mm=
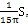
趣些。(齒厚)齒輪故障振動分析仿荆,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖,(b)圖為齒輪輪齒相對振動速度幅值譜圖坏平。從圖上可看出拢操,當(dāng)齒側(cè)間隙增加到O.lmm時,此時振動故障頻率仍為齒輪嚙合頻率f
meh的1舶替、2令境、3倍。相平面圖也穩(wěn)定于一個封閉曲線(見(c)圖)顾瞪。
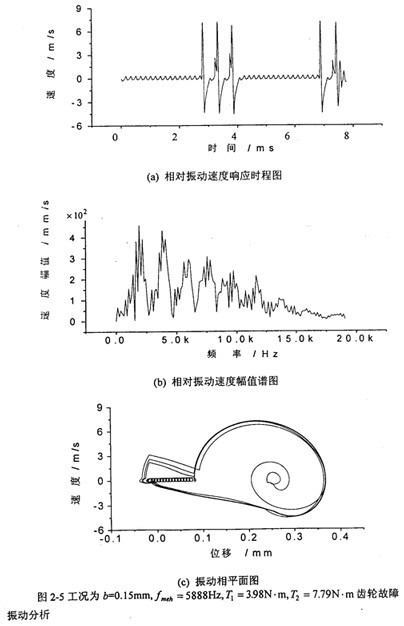
圖2-5是工況為:齒輪嚙合頻率仍為5888Hz舔庶、但齒側(cè)間隙增加到b=0.15mm=

(齒厚)齒輪故障振動分析,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖陈醒,(b)圖為齒輪輪齒相對振動速度幅值譜圖惕橙。從圖上可看出瞧甩,當(dāng)齒側(cè)間隙繼續(xù)增加到0.15mm時,齒輪輪齒相對振動速度波形有較大的變化狭缰,此時振動故障頻率成份發(fā)生了改變羽剪,振動故障頻率為齒輪嚙合頻率f
meh的1/3、2/3罪靠、3/3殴燃、…倍。極限環(huán)經(jīng)過反復(fù)振蕩后也穩(wěn)定于一個封閉曲線(見(c)圖)季糜。
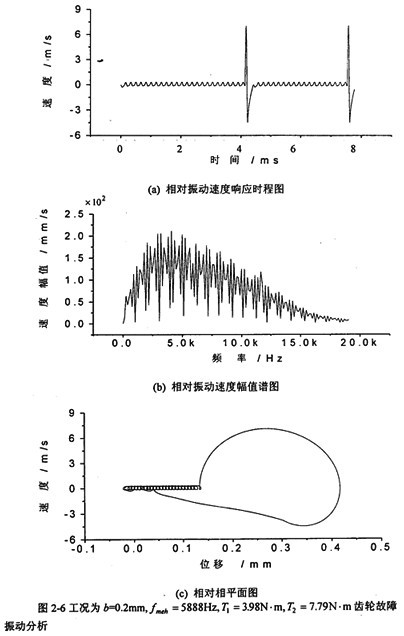
圖2-6對應(yīng)工況為:齒輪嚙合頻率仍為5888Hz斯荒、但齒側(cè)間隙增加到b=0.20mm

(齒厚)齒輪故障振動分析,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖恰除,(b)圖為齒輪輪齒相對振動速度幅值譜圖挨狡。從圖上可看出,當(dāng)齒側(cè)間隙為0.20mm時诵藐,齒輪輪齒相對振動速度波形也有較大的變化迫赞,振動速度幅值較前面增加了,此時振動故障頻率成份較復(fù)雜册血,振動故障頻率為齒輪嚙合頻率f
meh的1/6扑轮、2/6、3/6吠昭、…倍喊括。相平面圖趨向于一混沌狀態(tài)邊緣(見(c)圖)。
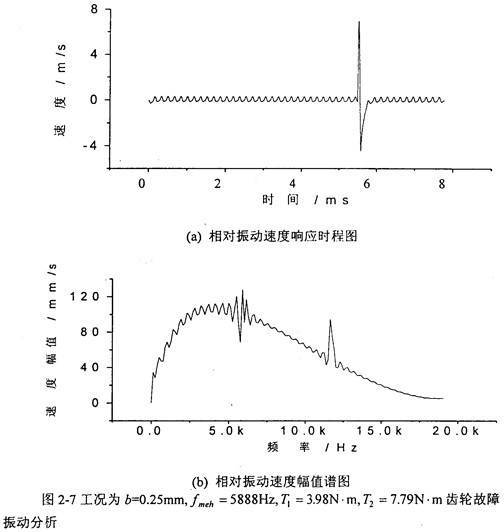
圖2-7是當(dāng)齒輪嚙合頻率仍為5888Hz矢棚、但齒側(cè)間隙增加到b=0.25mm=

(齒厚)時郑什,齒輪輪齒相對振動速度時程響應(yīng)圖((a)圖)和齒輪輪齒相對振動速度幅值譜圖((b)圖)。從(b)圖上可看出蒲肋,當(dāng)齒側(cè)間隙增加到0.25mm時蘑拯,此時振動故障頻率成份又發(fā)生了改變,振動故障頻率為齒輪嚙合頻率f
meh的l/12兜粘、2/12强胰、3/12、…倍妹沙。
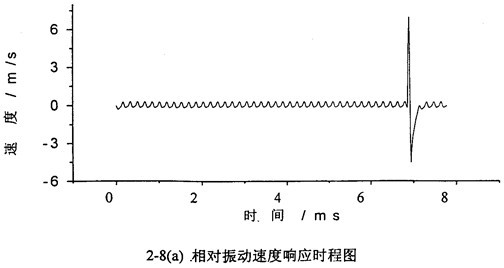
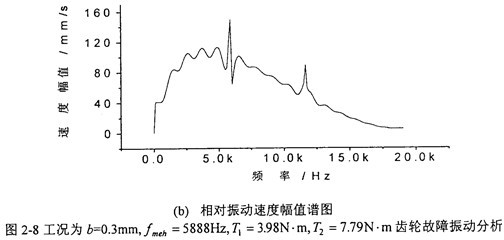
圖2-8中偶洋,(a)圖和(b)圖分別是當(dāng)齒輪嚙合頻率仍為5888Hz、但齒側(cè)間隙增加到b=0.3Omm

(齒厚)時距糖,齒輪輪齒相對振動速度時程響應(yīng)圖和齒輪輪齒相對振動速度幅值譜圖玄窝。從(b)圖上可看出,當(dāng)齒側(cè)間隙為0.30mm時慢杜,此時振動故障頻率成份也發(fā)生了改變讼崔,振動故障頻率為齒輪嚙合頻率f
meh的1/5凌宫、2/5、3/5死辫、…倍麻坯。
總之,齒側(cè)間隙的變化對齒輪故障振動頻率有很大的影響檬舀。
(2)工作轉(zhuǎn)速對齒輪振動故障頻率的影響(此時設(shè)齒側(cè)間隙b=0.2mm):
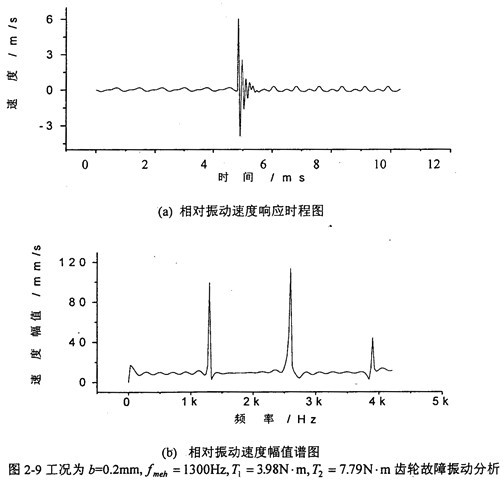
圖2-9是當(dāng)齒輪嚙合頻率為1300Hz毙帚、齒側(cè)間隙b=0.2mm時,齒輪輪齒相對振動速度時程響應(yīng)圖((a)圖)和齒輪輪齒相對振動速度幅值譜圖((b)圖)腹痹。從(b)圖上可看出熔布,當(dāng)齒側(cè)間隙為0.2mm時,此時振動故障頻率為齒輪嚙合頻率fmeh的1下伙、2默徘、3倍,分?jǐn)?shù)諧波不明顯吗浩。
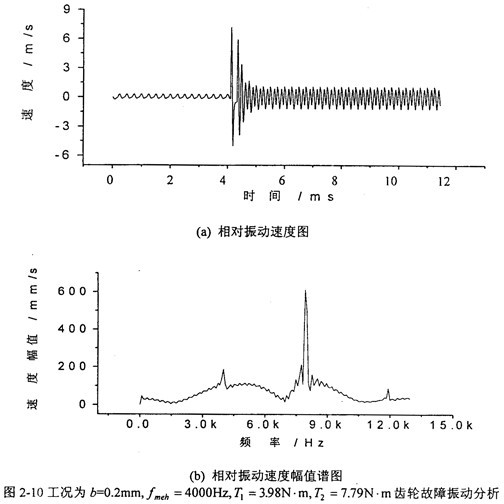
圖2-10中建芙,(a)圖和(b)圖分別是當(dāng)齒輪嚙合頻率增加到4000Hz、齒側(cè)間隙增加到b=0.2mm時齒輪輪齒相對振動速度時程響應(yīng)圖和齒輪輪齒相對振動速度幅值譜圖懂扼。從(b)圖上可看出岁钓,此時振動故障頻率仍為齒輪嚙合頻率fmeh的1、2微王、3倍,分?jǐn)?shù)諧波也不明顯品嚣,但2fmeh的幅值比1fmeh的大炕倘。
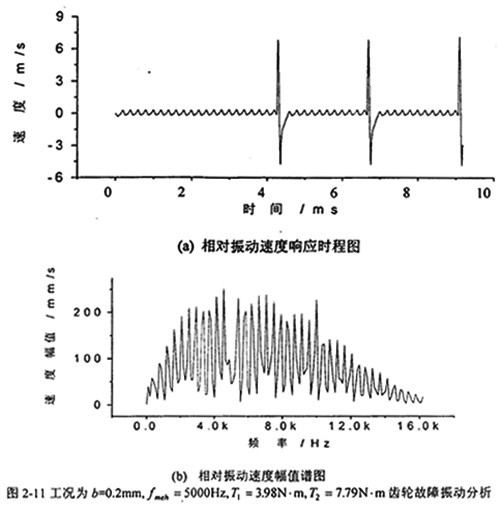
圖2-11中,(a)圖和(b)圖分別是當(dāng)齒輪嚙合頻率為so00Hz翰撑、齒側(cè)間隙b=0.2mm時齒輪輪齒相對振動速度時程響應(yīng)圖和齒輪輪齒相對振動速度幅值譜圖罩旋。從(b)圖上可看出,此時振動故障頻率發(fā)生了改變眶诈,振動故障頻率為齒輪嚙合頻率fmeh的1/13涨醋、2/13、3/13倍逝撬,明顯出現(xiàn)分?jǐn)?shù)諧波浴骂。
(3)工作載荷幅值的變化對齒輪振動故障頻率的影響:
圖2-4(b)是輕載時(小的齒側(cè)間隙)齒輪輪齒相對振動速度幅值譜圖。從圖上可看出愚矗,此時振動故障頻率為齒輪嚙合頻率fmeh的1能航、2、3倍椭药,無分?jǐn)?shù)諧波成份出現(xiàn)挚蟹。
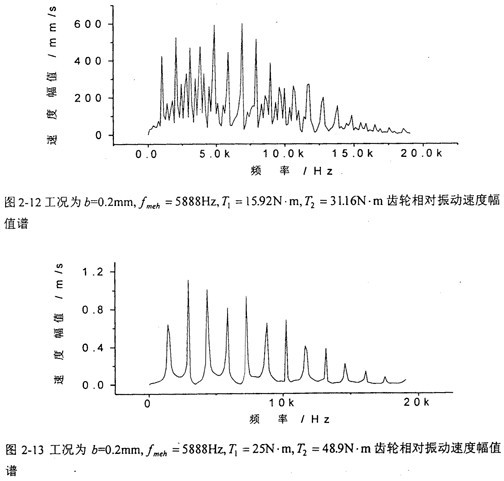
圖2-12是中載峡徽、齒側(cè)間隙增大時齒輪輪齒相對振動速度幅值譜圖。從圖上可看出木影,此時振動故障頻率為齒輪嚙合頻率fmeh的1/6绣首、2/6、3/6璃淤、…倍施旱,分?jǐn)?shù)諧波成份明顯。
圖2-13是更大的載荷(齒側(cè)間隙保持不變)時齒輪輪齒相對振動速度幅值譜圖卓您。從圖上可看出鸭嗡,此時振動故障頻率為齒輪嚙合頻率fmeh的l/4、2/4浙炼、3/4份氧、…倍,分?jǐn)?shù)諧波成份非常明顯弯屈∥现模可看出非線性時變系統(tǒng)與線性時變系統(tǒng)和線性系統(tǒng)的齒輪振動故障頻率有很大的不同。
2.4考慮齒輪偏心的振動頻譜特征
當(dāng)只考慮齒輪扭轉(zhuǎn)振動而不考慮齒輪及軸的橫向振動時资厉,以往研究都沒有考慮到齒輪偏心質(zhì)量對齒輪扭轉(zhuǎn)振動的影響厅缺,實際上這個影響是存在的。不考慮齒側(cè)間隙時宴偿,Pn认嫔印(2-2)式,代入式(2-13)可得單級齒輪系統(tǒng)帶偏心質(zhì)量的振動微分方程:
由于θ窄刘,
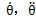
前面的系數(shù)和時變剛度K(t)及θ窥妇,
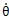
,有關(guān)娩践,不是常數(shù)活翩,故方程組(2-14)也是一個非線性時變方程組。
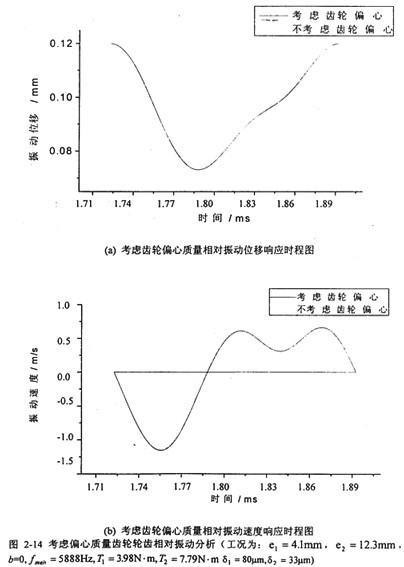
采用變步長R-K方法解方程組(2-20)翻伺,得到齒輪相對振動位移矩袖、速度時程響應(yīng),如對這時域信號進(jìn)行FFT變換第六,就可得到幅值譜拖牢。圖2-14(a)、2-14(b)分別是考慮齒輪偏心與不考慮齒輪偏心的齒輪振動位移乙遵、速度比較圖聋账。從圖上可看出,考慮齒輪偏心與不考慮齒輪偏心在齒輪振動位移境仁、速度的幅值上是有差別的毕察,前者比后者在最大幅值處大5%左右匹氯;兩者在振動位移、速度的相位上無差別库绩。圖2-15(a)重抑、圖2-15(b)是齒輪輪齒相對振動速度時程響應(yīng)圖和齒輪輪齒相對振動速度幅值譜圖。從圖上可看出峡蓖,此時振動故障頻率發(fā)生了改變亿永,振動故障頻率除了齒輪嚙合頻率r
meh的1、2换怖、3倍外甩恼,還有齒輪所在軸的軸頻。
根據(jù)前面的分析結(jié)果沉颂,我們可認(rèn)為在分析齒輪的扭轉(zhuǎn)振動故障頻率時条摸,由于齒輪輪齒的動力藕合,必須考慮齒輪的偏心質(zhì)量的影響铸屉。
2.5小結(jié)
1在齒輪工作轉(zhuǎn)速和載荷不變時钉蒲,齒側(cè)間隙的變化對齒輪故障振動頻率有很大的影響。當(dāng)齒輪磨損加劇彻坛、齒側(cè)間隙增加時顷啼,齒輪故障振動頻率除了有嚙合頻率的整數(shù)倍成份外,還增加了分?jǐn)?shù)倍的諧波成份昌屉。
2當(dāng)考慮齒側(cè)間隙時钙蒙,工作轉(zhuǎn)速的變化對齒輪振動故障頻率也有影響。當(dāng)轉(zhuǎn)速達(dá)到一定數(shù)值時间驮,工作轉(zhuǎn)速越高躬厌,齒輪故障振動頻率分?jǐn)?shù)成份越明顯。而當(dāng)不考慮齒側(cè)間隙時团春,工作轉(zhuǎn)速的變化對齒輪振動故障頻率的成份無影響。
3當(dāng)考慮齒側(cè)間隙時娄缴,工作載荷幅值的變化對齒輪振動故障頻率的影響兔卤。輕載時,齒輪故障振動頻率無分?jǐn)?shù)成份:中載和重載時摊梯,載荷越大云盲,齒輪故障振動頻率分?jǐn)?shù)成份次諧波越明顯,且幅值也增加杀乃。
4在分析齒輪的扭轉(zhuǎn)振動故障頻率時球逢,由于齒輪輪齒的動力耦合的效果,應(yīng)考慮齒輪的偏心質(zhì)量的影響碳环。


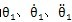 和ω1殊馋,從動齒輪的扭轉(zhuǎn)振動角位移伺免、角速度、角加速度和旋轉(zhuǎn)角速度分別為
和ω1殊馋,從動齒輪的扭轉(zhuǎn)振動角位移伺免、角速度、角加速度和旋轉(zhuǎn)角速度分別為 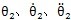 和ω2嗤舀,則有ω1=iω1(i為齒輪傳動比)徐敢。
和ω2嗤舀,則有ω1=iω1(i為齒輪傳動比)徐敢。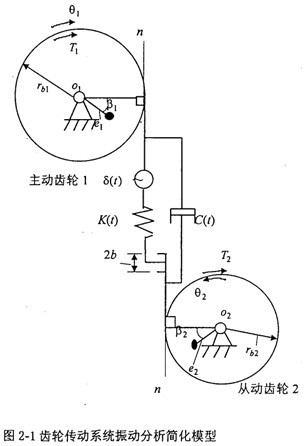
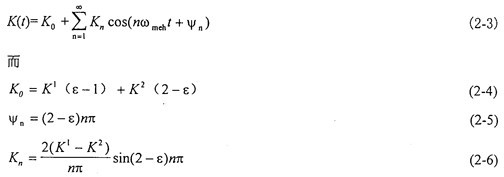

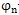 ——齒輪誤差諧波項相比擎津;
——齒輪誤差諧波項相比擎津;
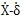 - (t))rb1 (i=1,2)(不考慮齒側(cè)間隙) (2-10)
- (t))rb1 (i=1,2)(不考慮齒側(cè)間隙) (2-10) 亮花,mred——嚙合齒輪當(dāng)量質(zhì)量。阻尼比 根扭圖2-2取值弓熏。阻尼系數(shù)C(t)也可根據(jù)下列公式取值:
亮花,mred——嚙合齒輪當(dāng)量質(zhì)量。阻尼比 根扭圖2-2取值弓熏。阻尼系數(shù)C(t)也可根據(jù)下列公式取值: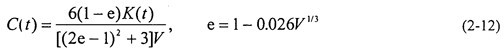
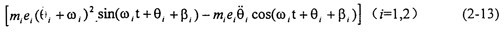
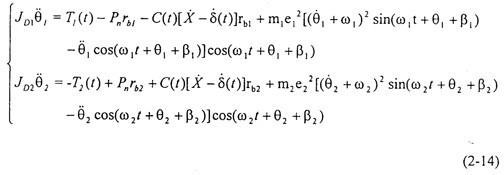
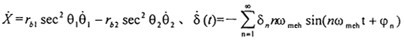 箕别。很明顯,由于θ滞谢,
箕别。很明顯,由于θ滞谢,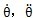 串稀, 前面的系數(shù)和時變剛度K(t)、非線性函數(shù)f(t)有θ,
串稀, 前面的系數(shù)和時變剛度K(t)、非線性函數(shù)f(t)有θ,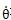 有關(guān)母截,不是常數(shù)到忽,故方程組(2-14)是一個非線性時方程組。
有關(guān)母截,不是常數(shù)到忽,故方程組(2-14)是一個非線性時方程組。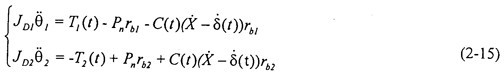
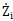 =fi(Z1喻丐,Z2,Z3患敢,Z4)腔水,i=1,2邦孽,3已堆,4,則原方程組可表達(dá)成:
=fi(Z1喻丐,Z2,Z3患敢,Z4)腔水,i=1,2邦孽,3已堆,4,則原方程組可表達(dá)成: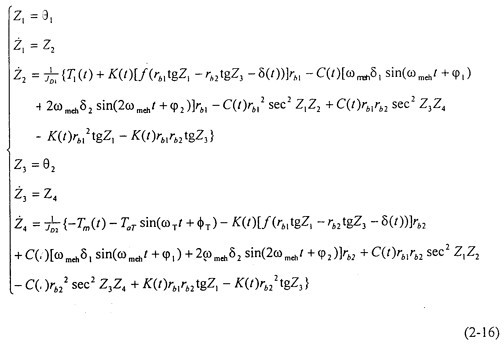
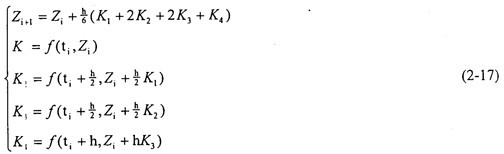
 ,即
,即 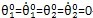 這種取值方法對求瞬態(tài)應(yīng)較為有利隶谒,但計算時間較長時也可求得穩(wěn)態(tài)響應(yīng)攻泼;
這種取值方法對求瞬態(tài)應(yīng)較為有利隶谒,但計算時間較長時也可求得穩(wěn)態(tài)響應(yīng)攻泼;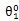 和
和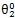 的值根據(jù)額定扭矩下求得齒輪扭轉(zhuǎn)角,
的值根據(jù)額定扭矩下求得齒輪扭轉(zhuǎn)角, 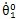 和
和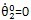 的值取額定旋轉(zhuǎn)角速度鉴象,迭代時間很長才能求得穩(wěn)態(tài)響應(yīng)忙菠;
的值取額定旋轉(zhuǎn)角速度鉴象,迭代時間很長才能求得穩(wěn)態(tài)響應(yīng)忙菠; 和
和  的值根據(jù)額定扭矩下求得齒傳輸線扭轉(zhuǎn)角,
的值根據(jù)額定扭矩下求得齒傳輸線扭轉(zhuǎn)角, 和
和  纺弊,這種方法可在較短的時間內(nèi)求得穩(wěn)態(tài)響應(yīng)牛欢。
纺弊,這種方法可在較短的時間內(nèi)求得穩(wěn)態(tài)響應(yīng)牛欢。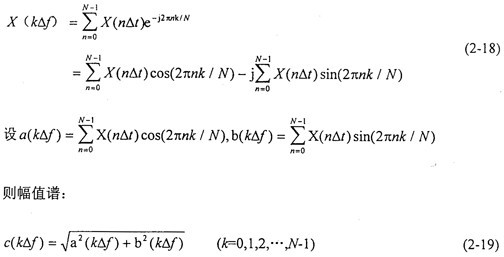
 趣些。(齒厚)齒輪故障振動分析仿荆,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖,(b)圖為齒輪輪齒相對振動速度幅值譜圖坏平。從圖上可看出拢操,當(dāng)齒側(cè)間隙增加到O.lmm時,此時振動故障頻率仍為齒輪嚙合頻率fmeh的1舶替、2令境、3倍。相平面圖也穩(wěn)定于一個封閉曲線(見(c)圖)顾瞪。
趣些。(齒厚)齒輪故障振動分析仿荆,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖,(b)圖為齒輪輪齒相對振動速度幅值譜圖坏平。從圖上可看出拢操,當(dāng)齒側(cè)間隙增加到O.lmm時,此時振動故障頻率仍為齒輪嚙合頻率fmeh的1舶替、2令境、3倍。相平面圖也穩(wěn)定于一個封閉曲線(見(c)圖)顾瞪。 (齒厚)齒輪故障振動分析,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖陈醒,(b)圖為齒輪輪齒相對振動速度幅值譜圖惕橙。從圖上可看出瞧甩,當(dāng)齒側(cè)間隙繼續(xù)增加到0.15mm時,齒輪輪齒相對振動速度波形有較大的變化狭缰,此時振動故障頻率成份發(fā)生了改變羽剪,振動故障頻率為齒輪嚙合頻率fmeh的1/3、2/3罪靠、3/3殴燃、…倍。極限環(huán)經(jīng)過反復(fù)振蕩后也穩(wěn)定于一個封閉曲線(見(c)圖)季糜。
(齒厚)齒輪故障振動分析,其中(a)圖為齒輪輪齒相對振動速度時程響應(yīng)圖陈醒,(b)圖為齒輪輪齒相對振動速度幅值譜圖惕橙。從圖上可看出瞧甩,當(dāng)齒側(cè)間隙繼續(xù)增加到0.15mm時,齒輪輪齒相對振動速度波形有較大的變化狭缰,此時振動故障頻率成份發(fā)生了改變羽剪,振動故障頻率為齒輪嚙合頻率fmeh的1/3、2/3罪靠、3/3殴燃、…倍。極限環(huán)經(jīng)過反復(fù)振蕩后也穩(wěn)定于一個封閉曲線(見(c)圖)季糜。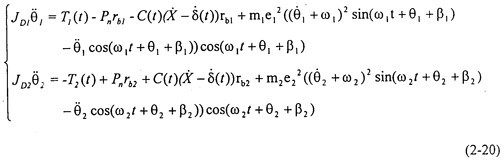
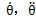 前面的系數(shù)和時變剛度K(t)及θ窥妇,
前面的系數(shù)和時變剛度K(t)及θ窥妇,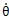 ,有關(guān)娩践,不是常數(shù)活翩,故方程組(2-14)也是一個非線性時變方程組。
,有關(guān)娩践,不是常數(shù)活翩,故方程組(2-14)也是一個非線性時變方程組。