管道穩(wěn)態(tài)裂紋擴(kuò)展模擬
2.1斷裂動力學(xué)理論簡述
斷裂力學(xué)學(xué)科的先導(dǎo)者是A.A.Griffith,他在1920年首先提出將裂紋臨界擴(kuò)展的判據(jù)與裂紋的長度定量地聯(lián)系在一起痘番,建立起脆斷理論的基本框架捉片。斷裂力學(xué)的蓬勃發(fā)展則以1948年Irwin和Orowan分別獨(dú)立建立的工程材料脆性斷裂理論為標(biāo)志。
作為斷裂力學(xué)的一個重要分支汞舱,斷裂動力學(xué)誕生的標(biāo)志是1948年英國物理學(xué)家N.F.Mott在Griffith理論中考慮動能的影響后所發(fā)表的論文伍纫。1951年印度女科學(xué)家Elizabeth Yoffe最早給出了運(yùn)動Griffith裂紋的解析解。然而斷裂動力學(xué)中最重要基本概念的提出昂芜,系統(tǒng)分析方法的形成莹规,以及相對成熟的實驗研究方法的建立,是20世紀(jì)80年代以來的研究成果泌神。本文的主旨是用數(shù)值模擬和實驗方法解決管道動態(tài)斷裂評估問題良漱。
2.1.1靜止裂紋與動態(tài)擴(kuò)展
斷裂力學(xué)認(rèn)為在結(jié)構(gòu)中不可避免有類似裂紋的缺陷存在。在小變形棠裹、低能量耗散的情況下忆和,可看作脆性斷裂;對于大變形效迹、高能量耗散的情況則按延性斷裂來處理龟聊。受應(yīng)力集中影響,除去理想脆性材料外啰蕴,外加載荷在裂紋尖端附近均伴隨非彈性區(qū)暑吹。若該區(qū)域尺寸與其他特征尺寸相比為小量,則可以用線彈性斷裂力學(xué)處理码承。裂紋根據(jù)加載方式的不同可分為三種模型:張開模式(I型)凄跑;滑開模式(Ⅱ型);撕開模式(Ⅲ型)城离。本文討論的范圍限于I型裂紋琢喷。在斷裂力學(xué)中,定義引起裂紋產(chǎn)生單位長度的擴(kuò)展所需要的能量為裂紋驅(qū)動力G那惜。在平面問題中算行,G與應(yīng)力強(qiáng)度因子Kc的關(guān)系可以表達(dá)為:
對于平面應(yīng)力問題梧油,E′=E;對于平面應(yīng)變問題州邢,E′=E/(1-v2)儡陨。其中,E是材料的楊氏模量量淌,v為泊松比骗村。
斷裂動力學(xué)(FractUre Dynamics)也叫做動態(tài)斷裂力學(xué)(Dynamic Fracture
Mechanics),其目的是研究那些慣性效應(yīng)不能忽略的斷裂力學(xué)問題呀枢。這些問題主要?dú)w納為兩大類:一是裂紋穩(wěn)定而外力隨時間迅速變化胚股,如振動、沖擊裙秋、波動等:二是外力恒定或緩漫變化而裂紋發(fā)生快速傳播琅拌。這兩類斷裂動力學(xué)的問題分別稱為裂紋動態(tài)起始問題和運(yùn)動裂紋問題。
運(yùn)動裂紋問題從現(xiàn)象上看可以分為前期加速摘刑,擴(kuò)展軌跡进宝,擴(kuò)展速度,分叉和止裂幾方面問題枷恕。本文研究裂紋從快速擴(kuò)展開始直至止裂的過程佩嘀。
2.1.2裂紋擴(kuò)展的極限速度
輸氣管道上的脆性裂紋擴(kuò)展速度曾經(jīng)達(dá)到過103m/s而S的量級。通過改善鋼材韌性遵艰,降低韌脆轉(zhuǎn)換溫度等辦法沫杜,裂紋擴(kuò)展的主要形式由脆性斷裂轉(zhuǎn)化為延性斷裂,裂紋擴(kuò)展速度也有大幅度的下降电摔。伴隨著超高壓管道上的裂紋擴(kuò)展晶乘,近年來的實測速度又有上升。
對于本文的裂紋動態(tài)模擬和止裂評估辱闺,裂紋擴(kuò)展速度是關(guān)鍵變化量翠笛。那么裂紋擴(kuò)展存在極限速度嗎?如果存在狈榛,如何量化桦徘?本小節(jié)旨在探討這方面的內(nèi)容。尤其針對輸氣管道上的應(yīng)用纽他,文中給出了大致的估算橄文。
1948年Mott認(rèn)為快速裂紋擴(kuò)展過程中的動能作用不可忽略∠翊罚考慮無窮大彈性板中的裂紋擴(kuò)展上陕,加入動能項的能量平衡方程為:

式中a為半個裂紋長度,U為彈性應(yīng)變能拓春,K為動能释簿,Γ為表面能亚隅。
在推導(dǎo)動能表達(dá)式的過程中,Mott引入以下假定:
●圍繞裂紋尖端區(qū)域的應(yīng)力場庶溶、位移場煮纵,可由靜態(tài)彈性理論確定;
●裂紋擴(kuò)展速度遠(yuǎn)小于柱形桿縱波速度C
o=

偏螺;
●裂紋擴(kuò)展阻力不隨裂紋速度變化而改變行疏。
在上述假定的前提下,得到無限大彈性板中的動能表達(dá)式:
式中k是待定的比例系數(shù)套像,p為密度酿联,v為裂紋擴(kuò)展速率,σ為無窮遠(yuǎn)處承受的均勻拉伸應(yīng)力夺巩,E為材料的楊氏模量贞让。
對于無限大板中的裂紋而言,應(yīng)變能U和表面能廠的表達(dá)式同靜態(tài)清況相比沒有形式上的改變咳衣。將三種能量的表達(dá)式代入能量平衡方程(2-2),可得:
將單位面積的表面能廠用表示為臨界裂紋長度ac的形式服移,經(jīng)過Berry等人的修正故碱,得到裂紋速度的表達(dá)式:
Roberts(1954)用數(shù)值方法計算了泊松比v=0.25時的系數(shù)
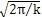
=0.38,從而得到鋼材中的極限裂速v
m≈1929m/s。
在雙懸臂梁DCB(double-Cantilever-Beam)試樣中測到的結(jié)果比上述值略低驶恨,約為1500m/s炎殃。
Freund(1972)通過分析推導(dǎo),認(rèn)為裂紋的極限裂速v
m道婚,應(yīng)該等于Rayleigh波速C
R件牧。按此方法估算,v=0.25時鋼材中的極限裂速v
m=294m/s潦博。
根據(jù)Rice(2000)通過奇異裂紋模型做出的最新論斷侮压,在典型的遠(yuǎn)場加載條件下,在I型和Ⅱ型時的極限速度為Rayleigh波速竖怯,而在Ⅲ型時的極限速度可達(dá)橫波波速蠕膀,對鋼材而言約3100m/s。
Rice總結(jié)了I型拉伸裂紋的實驗觀測結(jié)果胀茵,發(fā)現(xiàn):
●在脆性非晶態(tài)材料(如玻璃社露、PMMA)中,裂紋速度的上限為0.55CR~0.65CR;
●裂紋速度v<0.3CR~0.4CR時琼娘,斷裂面呈鏡面光滑狀峭弟。在更高(平均)速度時,裂紋表面變得非常粗糙脱拼,并且v開始劇烈振蕩瞒瘸;
●存在v接近于CR的例外情況坷备,如高度各向異性的脆性單晶(鎢、云母),及不完全燒結(jié)的固體挨务。
這一結(jié)果同鋼材斷裂從DBF到DDF的發(fā)展過程中击你,實測速度與斷口形貌的變化趨勢相吻合。簡單的說谎柄,就是韌性提高可以導(dǎo)致斷裂的極限速度降低丁侄。
壓力管道的裂紋擴(kuò)展與無限大彈性板不同,Kanninen等(1980)利用類似一維梁的模型提出了輸氣管道中的裂紋擴(kuò)展極限速度的估算值朝巫。模型中采用彈性基礎(chǔ)梁的撓度模擬在對稱載荷作用下圓柱殼的變形鸿摇,并作了以下基本假設(shè):
●以徑向變形為主;
●壓力沿圓周的變化可以忽略不計蒙亦;
●裂紋張開位移等于在裂紋區(qū)任何截面徑向位移沿圓周的積分皮卸;
●塑性屈服鉸在裂尖后部形成;
●裂紋擴(kuò)展速度超過流體降壓速度离饺,擴(kuò)展中裂尖后面的壓力為零猿池;
●由于裂紋出現(xiàn)導(dǎo)致殼體剛度突變。
得到管道裂紋的極限速度:
式中C0為柱形桿縱波波速疼尺,鋼材約5076m/s,h和R為管道壁厚和平均半徑罚蛾。按此式估算的西氣東輸管道上裂紋擴(kuò)展的極限速度約為648m/s。
對于裂紋在脆性管道中的快速擴(kuò)展氛侨,在全尺寸實驗中可觀察到的裂速范圍為600~1000m/s缩笤,考慮到不同的設(shè)計參數(shù),與上述預(yù)測比較接近汞潦;全尺寸實驗在近年來應(yīng)用的高韌性管線中觀測到的裂紋穩(wěn)態(tài)擴(kuò)展速度一般在150~350m/s,近似可以看作脆性斷裂速度的1/3殿恤,即:
在Kanninen之后,Emery(1950)提出演徘,盡管裂紋的起裂和小范圍擴(kuò)展可由系統(tǒng)的降壓值作為上限而加以估算慎陵,但開裂管道中的裂紋擴(kuò)展卻受到流體外流引起的壓力降低的強(qiáng)烈影響。在幾何尺寸一定的條件下喻奥,由管道斷裂引起的壓力釋放波可以由遠(yuǎn)端反射回來荆姆,從而增加了裂尖處的管道壓力:同時張開裂紋的自由邊,卻承受一個顯著減少的壓力映凳,致使裂紋擴(kuò)展減速胆筒。因此,為了解裂紋的動力學(xué)特征诈豌,必須考慮管道變形及流體壓力仆救。
在Emery的圓柱殼模型下,極限裂紋擴(kuò)展速度比(2-6)式略低矫渔。
2.1.3動態(tài)斷裂力學(xué)參數(shù)
斷裂動力學(xué)理論為結(jié)構(gòu)動態(tài)斷裂的分析與控制奠定了理論基礎(chǔ)彤蔽,并為其在工程應(yīng)用方面提供了重要的概念摧莽、分析方法、結(jié)構(gòu)參數(shù)計算和動態(tài)斷裂準(zhǔn)則顿痪∧髟基本概念可以歸納為三個方面:描述動態(tài)斷裂的特征參數(shù)、材料的動態(tài)斷裂韌性和運(yùn)動裂紋的止裂判據(jù)蚁袭。接下來對上述三方面問題掸柏,尤其是對于和管道問題相關(guān)的概念,加以闡述和介紹淆逛,以備后文直接引用椒玖。
本節(jié)的討論范圍限于I型裂紋快速擴(kuò)展問題,主要目的是給出與斷裂力學(xué)參數(shù)相應(yīng)的動態(tài)應(yīng)力強(qiáng)度因子倒你、動態(tài)能量釋放率和裂紋尖端張開角的表達(dá)式福荸。
2.1.3.1動態(tài)應(yīng)力強(qiáng)度因子
I型動態(tài)應(yīng)力強(qiáng)度因子

(t)的定義為:
式中t為時間葫辐,a
yy為y向正應(yīng)力分量窄栓。
自Yoffe(1951)開始硝僻,包括形Rice(1968)、Freund(1990)在內(nèi)的很多學(xué)者推導(dǎo)并不斷完善了無限大板等簡單模型的以

(t)表示的穩(wěn)態(tài)擴(kuò)展的裂紋頂端漸進(jìn)應(yīng)力場和位移場的解析解情键,Nishioka等(1996)進(jìn)而給出了包括瞬態(tài)情況下的四階漸進(jìn)展開式吵淌,在此不做贅述。
這樣只要得到

(t)的值肯拨,就可以按照上述文獻(xiàn)中的公式得到裂紋尖端場的解析解榕每。目前除對于無限介質(zhì)中的穩(wěn)態(tài)擴(kuò)展裂紋腹呀,通過適當(dāng)簡化可以得到應(yīng)力強(qiáng)度因子的解析表達(dá)式以外雪猪,有限介質(zhì)及構(gòu)件中運(yùn)動裂紋的動態(tài)應(yīng)力強(qiáng)度因子的計算主要依靠數(shù)值方法,包括有限元法和有限差分法起愈。
本文研究的高韌性鋼為彈塑性材料只恨,在裂紋擴(kuò)展前,往往在裂端區(qū)甚至更大范圍內(nèi)有相當(dāng)大的塑性變形抬虽,且伴隨著裂端后面的卸載官觅。因此,起裂后必須克服塑性變形才能發(fā)生裂紋擴(kuò)展阐污。此時休涤,作為衡量裂端區(qū)應(yīng)力場強(qiáng)度的力學(xué)參量J積分和應(yīng)力強(qiáng)度因子K并不是嚴(yán)格有效的。Kanninen提出了更先進(jìn)的J積分-T積分笛辟,適合應(yīng)用于在彈塑性材料中的動態(tài)裂紋擴(kuò)展分析功氨。
2.1.3.2動態(tài)能量釋放率
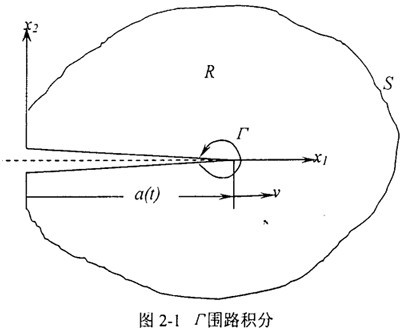
對含運(yùn)動裂紋的一般彈性體,為確定釋放到裂尖的能量手幢,考慮圍繞裂尖非常小的閉合回路Γ捷凄,如圖2-1所示忱详,動態(tài)能量釋放率可以由能量流動定義為:
式中vn表示裂紋尖端運(yùn)動速度在回路Γ上的法向分量,v為裂尖速率借睬,Ti為作用于Γ上的應(yīng)力分量阿座,W為應(yīng)變能密度,p為物質(zhì)密度奏宽。
這里Γ的形狀是任意的腮哩,但必須附關(guān)于裂尖的運(yùn)動坐標(biāo)系。這個表達(dá)式對線性與非線性的材料均適用踱措。
在裂紋穩(wěn)態(tài)擴(kuò)展的條件下晦苞,
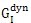
(t)退化為斷裂力學(xué)中的動態(tài)J積分,是與路徑無關(guān)的量:
對于無限介質(zhì)而言毕嘹,
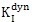
(t)和

(t)都可以寫成與裂紋速度有關(guān)的函數(shù)與靜態(tài)因子乘積的形式:

(t)=k(v)K(0)

(t)=g(v)G(0) (2-9)
將用動態(tài)應(yīng)力強(qiáng)度因子表示的無限大平面彈性體應(yīng)力場和位移場的表達(dá)式代入動態(tài)能量釋放率的定義式浊娄,可得二者之間的對應(yīng)關(guān)系:
式中F(v)可以表示為裂尖速率v與材料平面縱波波速C1及平面橫波波速C2的函數(shù),E是材料的楊氏模量沸幅,v為泊松比矗夯。
(2-10)式意味著

(t)和

(t)同時達(dá)到臨界值。也就是說聪弊,動態(tài)擴(kuò)展斷裂判據(jù)既可用臨界應(yīng)力強(qiáng)度因子施翰,也可用臨界能量釋放率來表示。這是對線彈性材料购城、恒定裂速擴(kuò)展的裂紋在無限大彈性體中得出的結(jié)論吕座,可以定性地推廣到一般問題中使用。
2.1.3.3裂紋尖端張開角
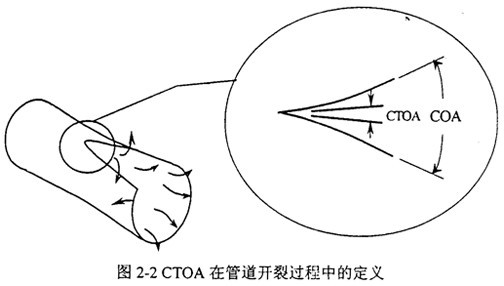
裂紋尖端張開角CTOA(Crack Tip Opening Angle)最早被用來分析核電站管路的穩(wěn)態(tài)裂紋擴(kuò)展瘪板,后來用于輸氣管線和航空工業(yè)吴趴。如圖2-2,與裂紋張開角COA不同侮攀,CTOA對應(yīng)于一定的斷裂擴(kuò)展?fàn)顟B(tài)锣枝,不隨測量點(diǎn)的位置而改變。CTOA在數(shù)學(xué)上可以按下式定義:
式中:δt為裂紋尖端張開位移兰英,△a為裂紋擴(kuò)展長度撇叁。
2.1.4材料的動態(tài)斷裂韌性
作為材料抵抗動態(tài)斷裂能力的度量,引入韌度的概念畦贸,稱為動態(tài)斷裂韌性陨闹。具體材料的韌性值由規(guī)定條件下的實驗測定。
表征材料抗力的動態(tài)斷裂參數(shù)有沖擊斷裂韌性KId薄坏,動態(tài)能量釋放率臨界值Gd趋厉,動態(tài)J積分臨界值Jd,裂紋尖端張開角臨界值(CTOA)c,甚至包括直接從實驗機(jī)上獲得的夏比沖擊功和落錘吸收能量等等桃铛,均可以作為判斷裂紋擴(kuò)展與止裂的參數(shù)肋森。工程上如何選用要視具體問題與實驗條件而定。
動態(tài)韌性參數(shù)除與靜態(tài)斷裂韌性同樣與材料性質(zhì)假磺,環(huán)境溫度烈杠,應(yīng)力狀態(tài)等因素有關(guān)以外,同時還與裂紋速度有關(guān)努扶。這是本文關(guān)心的問題跃百。
裂紋發(fā)生快速運(yùn)動時,一個高應(yīng)力集中區(qū)被驅(qū)動穿過材料晦了,因此裂紋頂端附近的材料產(chǎn)生很高的應(yīng)變速率或加載速率患刻。在一般情形下,高加載速率使得材料變脆普统,因而抗力降低:另一方面杠锻,隨著裂紋速度的提高,由于裂紋頂端應(yīng)力場多軸化程度降低埋村,又增強(qiáng)了塑性效應(yīng)珍特,從而提高了材料的抗力。另外魔吐,快速擴(kuò)展引起的熱耗散使得裂紋頂端附近溫度上升扎筒,也會影響材料的抗斷性能。Eftis,Klaft(1965)和Barton,Mall(1960)等的實驗結(jié)果表明酬姆,動態(tài)斷裂韌性由裂紋起始擴(kuò)展的材料抗力開始下降嗜桌,當(dāng)裂紋速度達(dá)到一定值時,動態(tài)斷裂韌性又隨裂紋速度的增長而提高辞色,表明了前面分析的正確性骨宠。
在裂紋穩(wěn)態(tài)擴(kuò)展階段,CTOA達(dá)到臨界值而保持恒定不變淫僻,稱作(CTOA)c诱篷。(CTOA)c可在小試樣沖擊實驗中測得壶唤,并直接應(yīng)用到全尺寸管道的斷裂上雳灵。在描述斷裂性能方面,(CTOA)c是衡量延性斷裂擴(kuò)展抗力的指標(biāo)之一闸盔,它被認(rèn)為可以替代夏比沖擊韌性悯辙,以解決在高韌性管線上依賴后者而出現(xiàn)的重大偏差。
Kanninen等(1992)認(rèn)為满页,對于動態(tài)裂紋擴(kuò)展問題预署,Gd和(CTOA)c是最適合的斷裂韌性描述參數(shù),如表2-1。
表2-1斷裂力學(xué)基本處理方法
|
問題類型 |
應(yīng)用范圍 |
裂紋驅(qū)動力 |
斷裂韌性 |
|
線彈性 |
小范圍塑性屈服 |
K |
KC |
|
彈塑性 |
大范圍塑性屈服聂歹,微小裂紋擴(kuò)展 |
J |
JR |
|
動態(tài)非彈性 |
大變形野疟,裂紋快速長距離擴(kuò)展 |
G,CTOA |
Gd,(CTOA)c |
2.1.5運(yùn)動裂紋的止裂判據(jù)
含裂紋結(jié)構(gòu)在動載作用下將發(fā)生裂紋的起裂和擴(kuò)展乘步,導(dǎo)致結(jié)構(gòu)破壞或者發(fā)生止裂廷碴,產(chǎn)生這些過程的條件稱為判據(jù)。除了1.2,1節(jié)提到過的減壓波速判據(jù)及在它基礎(chǔ)上發(fā)展起來的雙曲線方法以外榨降,還有應(yīng)力強(qiáng)度因子K判據(jù)就用,能量釋放率G判據(jù)和裂紋尖端張開角CTOA判據(jù)等。表2-1同樣給出了參考性意見扇牢。
在止裂條件的建立上霉处,存在兩種不同的觀點(diǎn),即動態(tài)觀點(diǎn)和靜態(tài)觀點(diǎn)椰陋。下面用K判據(jù)為例介紹一下兩種觀點(diǎn)的區(qū)別和發(fā)展嫌松,以及本文的選擇。動態(tài)觀點(diǎn)認(rèn)為奕污,裂紋的快速擴(kuò)展直至止裂是一個完整的過程豆瘫,止裂是這種過程的結(jié)束,并忽略慣性力的影響菊值。這樣外驱,裂紋持續(xù)快速擴(kuò)展的條件為:

=K
ID(v,T) (2-12)
即把裂紋動態(tài)擴(kuò)展斷裂韌度KID表示成為裂紋速率v和溫度T的函數(shù)腻窒。注意這一條件并不適用于起裂時刻昵宇,因為KID(O,T刀不等于靜態(tài)韌性KIC(T)儿子。
按照上面的觀點(diǎn)瓦哎,從止裂發(fā)生的t
0時刻一直到裂紋速度降為零的t
a時刻,

加均應(yīng)小于擴(kuò)展斷裂韌度K
ID(v柔逼,T)的最小值蒋譬,止裂判據(jù)表示為:
這樣,通過數(shù)值方法解出特定問題的K
I(t)愉适,和材料實驗定出的K
ID(v寓蔼,T)相比較,可以得到是否滿足止裂條件的結(jié)論韩艾。
靜態(tài)觀點(diǎn)著眼于止裂瞬間的裂紋尖端條件筛六,而不顧及已經(jīng)發(fā)生的裂紋動態(tài)擴(kuò)展過程和歷史。這樣吭芯,基于靜態(tài)觀點(diǎn)的止裂判據(jù)表示為:
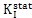
≤K
Ia (2-14)
式中

是對應(yīng)于止裂長度的靜態(tài)應(yīng)力強(qiáng)度因子通溜,K
Ia是材料的靜態(tài)斷裂韌性。兩種學(xué)術(shù)觀點(diǎn)的爭論長達(dá)二十多年,并都得到了特定條件下實驗結(jié)果的證實溪毕。直至1985年方達(dá)成一致胃琴,解釋如下:
引起動態(tài)效應(yīng)的主要原因是由于試樣邊界對應(yīng)力波的反射,當(dāng)邊界反射的應(yīng)力波幾乎不返回到裂紋尖端的情況下穿汽,采用靜態(tài)觀點(diǎn)相對合適洽咬;反之應(yīng)采用動態(tài)止裂分析觀點(diǎn)。這一結(jié)論得到了實驗的證明倚务。
壓力管道尤其是高壓輸氣管道上的裂紋擴(kuò)展是強(qiáng)幾何非線性的過程橙围,同時不斷伴隨應(yīng)力波的傳播與反射,因而本文在分析裂紋擴(kuò)展與止裂時用了動裂紋約束的概念(動態(tài)觀點(diǎn))着逐。根據(jù)這一概念崔赌,裂紋止裂就是使裂紋不能連續(xù)擴(kuò)展。現(xiàn)將本文用到的以G和CTOA建立的動態(tài)判據(jù)分述如下:
對于天然氣管道耸别,能量釋放率判據(jù)可以表示為:
G(a,p,D,SDR,E)=G
d(T,v,h) (2-15)
式(2-15)中健芭,當(dāng)Gmax=Gd時,裂紋擴(kuò)展秀姐;若G<Gdmin慈迈,裂紋止裂。G表示裂紋驅(qū)動力省有,Gd表示材料的動態(tài)斷裂韌性痒留,a為裂紋長度,p為流體壓力蠢沿,D為管道直徑伸头,SDR(Standard Dimension Ratio)為管道外直徑與壁厚的比值,E為材料的楊氏模量舷蟀,T為溫度恤磷,v為裂紋擴(kuò)展速率,h為試樣壁厚戈勾。
為了防止裂紋在工程管道上擴(kuò)展事故的發(fā)生绷煎,G和Gd的相對值為實際應(yīng)用準(zhǔn)則提供了定量的形式。G來源于對結(jié)構(gòu)模型的分析和計算户痒,而Gd要通過對結(jié)構(gòu)材料的實驗來分析確定火毕。
類似的,在管道延性裂紋擴(kuò)展過程中聪萨,表征裂紋驅(qū)動力的(CTOA)max與表征管壁斷裂韌性(CTOA)c構(gòu)成止裂判據(jù):
(CTOA)max(a,p,D,SDR,E)=(CTOA)c(T,v,h) (2-16)
當(dāng)(CTOA)max ≥(CTOA)c時假盼,裂紋擴(kuò)展肢糜;若(CTOA)max<(CTOA)c盘另,則裂紋止裂。
2.2斷裂動力學(xué)的有限元法
管道裂紋動態(tài)擴(kuò)展問題的關(guān)鍵是正確描述管道的實際工作狀態(tài)。斷裂動力學(xué)問題的復(fù)雜性和目前的研究深度決定了分析解法的求解必須對加載形式巩荧、材料參數(shù)抗海、裂紋幾何和運(yùn)動狀態(tài)作很多限制,因而本文以有限元方法為主福耐,在表征韌性的參數(shù)確定和計算結(jié)果參照中引入實驗手段葫羡,在試件比擬的塑性區(qū)范圍確定等處用到了解析方法。
斷裂動力學(xué)中的有限元法分為動力學(xué)分析和斷裂分析兩方面昌罩。在動力學(xué)分析中要考慮材料的慣性效應(yīng)哭懈,在動態(tài)變化的載荷下求解運(yùn)動方程;在斷裂分析方面茎用,要考慮裂紋尖端場的性質(zhì)遣总,以及裂紋擴(kuò)展引起的邊界變化等。下面分別從這兩方面介紹本文計算中用到的有限元技術(shù)及相關(guān)處理方法轨功。
2.2.1殼體結(jié)構(gòu)動力學(xué)基本方程
殼體有限元計算的一般思路是在單元內(nèi)描述問題旭斥,再根據(jù)節(jié)點(diǎn)集合。在描述幾何方程和運(yùn)動方程之前古涧,首先說明符號的格式垂券。本節(jié)將用到矢量符號、矩陣符號和上下標(biāo)羡滑。矢量符號通過黑體表示菇爪,如a,它的分量表示為:ai柒昏,也可以以矩陣{a}的形式表示娄帖。aiI是節(jié)點(diǎn)I的a矢量的第i個分量。
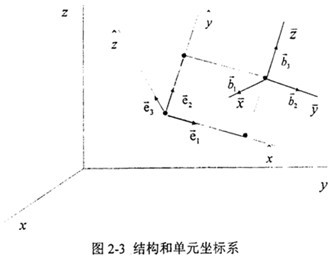
在本節(jié)中卜判,將會用到圖2-3所示的三種坐標(biāo)系:
●空間固定的總體坐標(biāo)系(x仔省,y,z)众攻,或x
i红集,正交基矢量為 。
●節(jié)點(diǎn)坐標(biāo)系行(
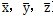
)習(xí)条稍,反映節(jié)點(diǎn)的平動與轉(zhuǎn)動判懒;正交基矢量為b
i。
●單元隨體坐標(biāo)系(
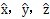
)悟惰;正交基矢量為e
i刀雳。
對于總體坐標(biāo)系中的任意矢量a,其在節(jié)點(diǎn)坐標(biāo)系中的分量可以表達(dá)為:
其中估曾,bxl粪世,byi馆义,bzl是節(jié)點(diǎn)基矢量bi在總體坐標(biāo)系中的三個分量。
類似地胁塞,對于單元隨體坐標(biāo)系:
其中[b]T咏尝、[e]T分別是總體坐標(biāo)與節(jié)點(diǎn)坐標(biāo)、總體坐標(biāo)與單元隨體坐標(biāo)之間的轉(zhuǎn)換矩陣啸罢。
節(jié)點(diǎn)J的初始位置為:
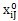
(i=1编检,2,3代表x扰才,y允懂,z三個方向的分量),當(dāng)發(fā)生了位移u
iJ后衩匣,新的位置坐標(biāo)為x
iJ累驮。
x
iJ=

+u
iJ (2-19)
2.2.1.1幾何方程
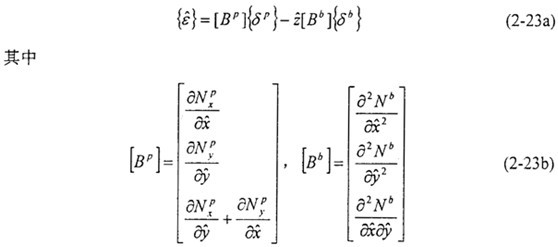
基于Kirchhoff假設(shè)的板殼單元,殼體中某一點(diǎn)的應(yīng)變
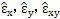
可以由中面應(yīng)變
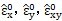
和曲率
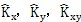
來表示:
其中[NP]為殼體面內(nèi)位移形函數(shù)舵揭,[Nb]為殼體彎曲位移形函數(shù)谤专。[δP]、[δb]是相應(yīng)的節(jié)點(diǎn)位移午绳。
將方程(2-22)代入(2-21)置侍,得到
2.2.1.2運(yùn)動方程
對于慣性力不可忽略的結(jié)構(gòu)進(jìn)行分析,要求解運(yùn)動方程拦焚,以獲得系統(tǒng)在瞬時狀態(tài)下的位移和速度瘫骏、加速度。一般的方法是按照平動和轉(zhuǎn)動的自由度荣吻,分別給出運(yùn)動方程哭夺。在有限元中,對于離散化的節(jié)點(diǎn)押辽,要相應(yīng)地給出它的三個平動方程和三個轉(zhuǎn)動方程卷撞。
三個平動方程為:
其中i代表節(jié)點(diǎn)號,m
i為節(jié)點(diǎn)質(zhì)量饵忙,
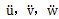
為平動加速度盐文,
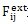
為外力,
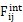
為變形引起的內(nèi)力(其中j=1岖疲,2咏摔,3,分別表示三個坐標(biāo)軸方向x极阴,y昙百,z)。
三個轉(zhuǎn)動方程為:
其中I
ij為轉(zhuǎn)動慣量碟狞,
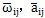
分別為角速度和角加速度啄枕,
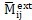
為外力矩婚陪,
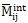
為變形引起的內(nèi)力矩。
公式(2-24)射亏,(2-25)中的內(nèi)力分量
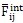
和

可以如下求得:
首先根據(jù)虛功原理近忙,在一個單元E內(nèi)竭业,對節(jié)點(diǎn)i有:
其中對I 不求和智润;;j代表各方向未辆,對j求和窟绷。
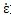
為單元E的應(yīng)變率,V是單元體積咐柜。由上述方程可以得到節(jié)點(diǎn)內(nèi)力和節(jié)點(diǎn)內(nèi)彎矩:
利用疊加原理兼蜈,將每一個單元內(nèi)的節(jié)點(diǎn)上的內(nèi)力和內(nèi)彎矩分別求和,可得到節(jié)點(diǎn)上的相應(yīng)分量:
其中拙友,
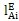
是如下定義的相關(guān)系靈敏:

=1 當(dāng)單元E中的節(jié)點(diǎn)A與節(jié)點(diǎn)i相關(guān)为狸;

=0 當(dāng)單元E中的節(jié)點(diǎn)A與節(jié)點(diǎn)i無關(guān)。
將方程(2-28)代入方程(2-24)和(2-25)遗契,可得到各節(jié)點(diǎn)的加速度與角加速度:
對于每一時間步長臭膊,由運(yùn)動方程首先解出各節(jié)點(diǎn)的平動加速度,然后根據(jù)顯式中心差分公式解出各節(jié)點(diǎn)速度:
利用位移可以根據(jù)幾何方程和本構(gòu)方程求得應(yīng)變和應(yīng)力膊编。
2.2.1.3本構(gòu)方程
本文研究鋼制管道的裂紋擴(kuò)展栏赋。忽略軋制過程的影響,鋼材可看作各向同性材料尸钢,則本構(gòu)關(guān)系可以寫成分段線性彈性的形式仙衩。進(jìn)一步考慮到本文采用節(jié)點(diǎn)力釋放法進(jìn)行裂紋擴(kuò)展計算,裂尖附近的應(yīng)力集中影響不大熔厌,故可采用線彈性本構(gòu)關(guān)系計算篇挡。
對于板殼單元,在單元隨體坐標(biāo)下應(yīng)變和應(yīng)力均只有三個分量:
2.2.1.4局部坐標(biāo)下的邊界條件
一般地誉煎,可以在邊界處約束任意平動與轉(zhuǎn)動分量姥胳,即令其為零。如要定義的運(yùn)動分量不在總體坐標(biāo)系下好啸,則需在該節(jié)點(diǎn)定義局部坐標(biāo)(X贵健,Y,Z)渊季。計處牙可以通過定義X和Y坐標(biāo)的方向余弦cxX朋蔫,cyX,czX却汉,cxY驯妄,cyY荷并,czY來實現(xiàn)。Z坐標(biāo)的方向余弦可通過其正交性由下式求得:
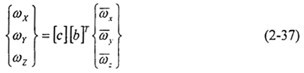
將上面的轉(zhuǎn)換矩陣定義為[c]青扔,則邊界條件中的平動速度可按(2-36)式轉(zhuǎn)化為局部坐標(biāo)中的分量源织,轉(zhuǎn)動角速度按下式定義:
然后將被約束的分量置零,求解微猖。求解后的平動速度和轉(zhuǎn)動速度可分別通過(2-36)和(2-37)的逆變換轉(zhuǎn)化成總體坐標(biāo)中的分量谈息。因為新的角位移量從方程(2-31)和關(guān)于b1的方程直接解得,邊界條件通常反映在更新的位移和節(jié)點(diǎn)向量b1中凛剥。
2.2.2斷裂動力學(xué)基本方程
2.2.2.1生成模式與擴(kuò)展模式
在管道裂紋擴(kuò)展問題中侠仇,因動態(tài)斷裂發(fā)生的時間很短,以及裂紋擴(kuò)展速度的非預(yù)先確定性犁珠,使得測量高階的物理量如能量分布逻炊、瞬時動態(tài)能量釋放率和動態(tài)裂紋尖端應(yīng)力場變得十分困難。為此針對管道快速斷裂問題發(fā)展了兩種分析計算模式:生成模式(Generation mode)和擴(kuò)展模式(Propagation mode)雇牍。
生成模式就是給定管道的幾何尺寸和工作條件嗅呻,同時必須給出已知的以裂紋擴(kuò)展長度或者裂紋速度表示的裂紋擴(kuò)展歷史作為補(bǔ)充條件使得問題可解,從而計算裂紋驅(qū)動力G(或CTOA和評估斷裂韌度Gd(或(CTOA)c)乌心。
本章計算中的裂紋擴(kuò)展速度取為定值导劝,該值未必是裂紋穩(wěn)態(tài)擴(kuò)展的真實速度。然而通過指定不同的速度值枕泽,可以尋找對應(yīng)于某一特定穩(wěn)態(tài)裂紋擴(kuò)展速度的G或CTOA往姆,如果該值小于材料韌性,可以判斷發(fā)生止裂掰站;否則可能發(fā)生擴(kuò)展宏湾。從而得到一些有價值的結(jié)論,例如在什么速度下管道失穩(wěn)斷裂等等涧谓。這種分析方法是運(yùn)用了生成模式旋稚。
擴(kuò)展模式是通過實驗測量裂紋速度和壓力分布,分析Gd(或(CTOA))瑟捺,找到它與裂紋速度之間的關(guān)系奕枝,分析確定產(chǎn)生裂紋擴(kuò)展需要的驅(qū)動力,從而得到一定條件下是否止裂的結(jié)論瓶堕。包括第一章提到的雙曲線法和后面提到的韌性減速機(jī)理等以實驗和結(jié)合實驗的計算為主的分析方法隘道,就是采用了擴(kuò)展模式。
2.2.2.2節(jié)點(diǎn)力釋放技術(shù)
節(jié)點(diǎn)力釋放(Node Foroe Release)郎笆,顧名思義就是當(dāng)裂紋頂端通過有限元網(wǎng)格中的某節(jié)點(diǎn)時谭梗,便解除該節(jié)點(diǎn)在網(wǎng)格中本來起到的連接作用,即將其分為兩個節(jié)點(diǎn)宛蚓,并釋放連接力激捏,如圖2-4设塔。
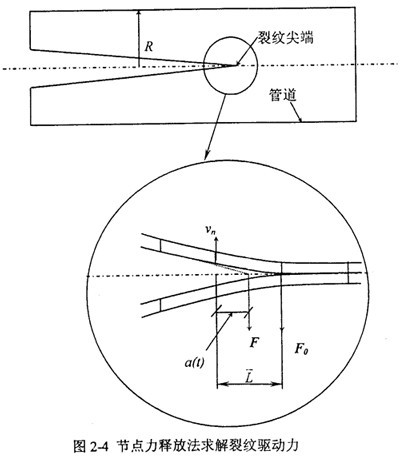
在典型的生成模式計算中,可根據(jù)指定的a(t)或v(t)判斷裂紋經(jīng)過的時間和路線远舅,依次釋放節(jié)點(diǎn)力闰蛔;另一種運(yùn)用擴(kuò)展模式的方法是通過判斷裂紋頂端被約束的節(jié)點(diǎn)力達(dá)到F
c時,這個節(jié)點(diǎn)便被松弛图柏。這里的F
c是指定的序六,它與網(wǎng)格尺寸以及動態(tài)斷裂韌性K
ID有關(guān)。Keergstra(1976)證明爆办,對于給定的網(wǎng)格揩臊,裂紋頂端的節(jié)點(diǎn)力正比于應(yīng)力強(qiáng)度因子K
ID嚎脖。
早期將有限元法應(yīng)用于動態(tài)裂紋擴(kuò)展時鬼痹,裂尖運(yùn)動由不連續(xù)的突進(jìn)進(jìn)行模擬:在時間增量△t內(nèi),裂尖沿裂紋方向從單元的一個節(jié)點(diǎn)改變到下一個節(jié)點(diǎn)勤鼓。為了得到比較精確的解答榕吨,必須采用較小的時間步長△t,通常為膨脹波在兩個最近單元節(jié)點(diǎn)間傳播所需要的時間涎舔。由于裂紋傳播速度通常明顯低于波速甲盘,在時間△t內(nèi)裂尖實際上通常只能運(yùn)動到兩個相鄰節(jié)點(diǎn)之間的某一位置。在裂尖從一個節(jié)點(diǎn)移動到下一個節(jié)點(diǎn)的過程中哮互,裂紋長度的突然增加和位移約束的突然解除臣镜,將引起有限元求解中比較嚴(yán)重的高頻振蕩現(xiàn)象。為了克服這一困難题晌,產(chǎn)生了“回復(fù)力”法洁馒,Lagrange乘子法,節(jié)點(diǎn)力釋放率法等緩步釋放節(jié)點(diǎn)的方法,下面介紹本文采用的節(jié)點(diǎn)力釋放率法儡皮。
在生成模式中柱锹,輸入信息包括作為時間函數(shù)的裂紋尖端位置,每一時間步長中裂紋前進(jìn)的距離是已知的丰包。裂紋沿著單元擴(kuò)展的過程中單元節(jié)點(diǎn)力逐步釋放禁熏,此時,能量釋放率G邑彪,即在裂端區(qū)每單位面積上裂紋擴(kuò)展所引起的能量變化瞧毙,可以近似地以節(jié)點(diǎn)力作功的形式表示:
式中,h是管理壁厚度寄症,
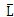
是沿裂紋擴(kuò)展方向的一個單元長度宙彪,△t是裂紋擴(kuò)展一個單元所用的時間,v
n是垂直裂紋擴(kuò)展方向的節(jié)點(diǎn)位移速度瘸爽,系數(shù)2表示管道對稱計算的兩個部分您访。
在公式(2-38)中铅忿,F(xiàn)是被釋放的約束力,它的大小隨著裂紋在單元邊界上的位置呈線性變化灵汪,表示為:
式中的Fo是被釋放的節(jié)點(diǎn)約束力檀训,a(t)是裂紋在單元上的擴(kuò)展長度。指數(shù)c曾取過1/2姆赔、1阅窝、3/2、2等不同取值豆凛。本文在與實驗對比的基礎(chǔ)上取1坞龙。
2.2.2.3裂紋驅(qū)動力G的能量表達(dá)
能量平衡方法計算裂紋驅(qū)動力基于Griffiths斷裂理論。在本章的計算程序中缸舱,外力作功和內(nèi)部能量的平衡常被用來校核計算結(jié)果的數(shù)值穩(wěn)定性蚀稻,也可將算得的能量值帶入Irwin-Orowan能量平衡公式計算裂紋驅(qū)動力。該方法與節(jié)點(diǎn)釋放法更為簡便把意。
Griffiths奠定了斷裂問題的能量平衡理論府塘。在裂紋擴(kuò)展過程中,物體內(nèi)部能量釋放所產(chǎn)生的裂紋驅(qū)動力導(dǎo)致了裂紋增長绿捶,同時存在阻止形成新裂紋面積的阻力棚疏,當(dāng)裂紋增長da長度時,二者形成平衡婆精。這樣裂紋驅(qū)動力G可以表示為:
式中h表示裂尖處材料厚度继溯,W表示外力作用于裂紋體的功,U表示應(yīng)變能沈条。在動裂紋擴(kuò)展問題中需要考慮動能K的作用需忿,上式擴(kuò)展為:
早期對流體壓力管道裂紋擴(kuò)展問題的分析中曾應(yīng)用應(yīng)變能變分原理,將裂紋動力等效為裂紋前面環(huán)向應(yīng)變能的釋放率拍鲤,Iewin-Conten發(fā)展了裂紋驅(qū)動力的解析計算:
式中p0為初始內(nèi)壓贴谎,D0和h為管壁外徑和壁厚,E為材料的楊氏模量季稳。
2.2.3數(shù)值穩(wěn)定性分析
在顯式時間積分中擅这,除非時間步長選得足夠小,否則會出現(xiàn)數(shù)值不穩(wěn)定性景鼠,從而使計算結(jié)果失去意義仲翎。盡管對于完全非線性問題,不能進(jìn)行穩(wěn)定性分析铛漓,但是經(jīng)驗表明線性分析也會給出有用的時間步長估計溯香。一般說來,將線性穩(wěn)定的時間步長減少10%到20%,可以克服非線性帶來的不穩(wěn)定性玫坛。
對于中心差分结笨,線性分析表明時間步長
其中,
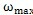
是系統(tǒng)的最高頻率傅慈, 是最高頻率下的臨界阻尼系數(shù)蹦虏。
ω是下面問題的特征值:
[K]{X}=ω
2[M]{X} (2-44)
其中[K]是系統(tǒng)的剛度矩陣,[M]是質(zhì)量矩陣碘淘。
在實際計算中刮血,我們并不是直接計算系統(tǒng)的ω
max,而是計算單元的
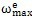
惰采。在所有的單元的

中選擇最大值作為ω
max颂鞭。
對于板單元,有
其中栋锣,Cl是平面縱波波速刑袒,對四邊形板單元來說,L是短邊的長度逃窜。
2.2.4氣體壓力模式
1.3.3節(jié)提到了解禍算法中氣體壓力模式的廣泛應(yīng)用郊舅。對于含裂紋擴(kuò)展的管道妒槐,其內(nèi)部管壁受到的氣體壓力由兩種模式組成:裂紋前面氣體減壓傳播和裂紋后部的氣體壓力衰減止骨。
Battelle的Maxey等人在實驗中采用壓縮空氣、氮?dú)庖约凹淄楹扛叩奶烊粴庥^察氣體的減壓行為吮铭,發(fā)現(xiàn)理想氣體規(guī)律足以滿足這些氣體的狀態(tài)等式时迫。假設(shè)氣體的膨脹過程是等熵過程,充滿氣體的管道突然發(fā)生開裂谓晌,整個狀態(tài)中氣體成分混和均勻掠拳,則裂尖附近氣體局部壓力與裂紋擴(kuò)展速度有如下關(guān)系:
式中p
d為減壓后的壓力水平(MPa);p
i為開裂前管內(nèi)壓力(MPa)纸肉;v為裂紋擴(kuò)展速度(m/s)溺欧;v
a為初始壓力和溫度狀態(tài)下的聲速(m/s);
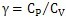
為起始狀態(tài)下氣體的絕熱系數(shù)柏肪,C
P和C
v分別為定壓比熱和定容比熱姐刁。
從(2-46)式可以看出,當(dāng)裂紋在管道上擴(kuò)展時烦味,裂紋前面的氣體減壓傳播聂使,其數(shù)值低于氣體初始壓力值p
0,氣壓減少值主要取決于裂紋的擴(kuò)展速度谬俄,對于穩(wěn)態(tài)擴(kuò)展的長裂紋柏靶,管道內(nèi)部氣體減壓趨于穩(wěn)定的數(shù)值。
當(dāng)裂紋沿管壁快速擴(kuò)展時,裂紋后面的氣體逸出铛田,氣壓降低挂蹦,但是與液體壓力不同的是,該區(qū)域內(nèi)的氣體壓力并不是立即降為零值嚣历,而是穩(wěn)定地衰減至大氣壓力盔连,并有一段明顯的衰減區(qū)。在這一衰減區(qū)內(nèi)阻羞,氣體壓力仍然作用在已經(jīng)開裂的管壁上凰染,加速管壁的變形。
根據(jù)實驗給出的實際管道開裂實驗的結(jié)果忘拧,發(fā)展了裂紋后面氣體壓力衰減模式捏诫,將氣壓的衰減表示成裂紋位置和初始壓力的函數(shù)。常見的衰減模式有指數(shù)衰減的Fourier級數(shù)和拋物線衰減函數(shù)等溃擒。
更為簡便的是圖2-5所示的氣體壓力衰減模式是線性衰減函數(shù)连定,圖中以裂紋擴(kuò)展方向z為橫軸,壓力分布p為縱軸叮洋,其計算表達(dá)式為
P(z)=P
1(1-

)磁携,z<L (2-47)
式中z是計算截面的位置,L是衰減長度良风。在計算中谊迄,L取1.5倍或2倍的管道外徑。
2.3管道穩(wěn)態(tài)裂紋擴(kuò)展問題的數(shù)值模擬
本節(jié)著重介紹穩(wěn)態(tài)擴(kuò)展條件下的開裂管道計算結(jié)果烟央,力求從多個角度模擬管道變形的真實狀態(tài)统诺,為建立止裂判據(jù)與后文的減速機(jī)理打下基礎(chǔ)。
2.3.1計算模型與邊界條件
管道上的裂紋一般從起裂點(diǎn)同時向兩側(cè)擴(kuò)展疑俭。因管道幾何形狀和載荷分布具有對稱性粮呢,本文取一側(cè)管道的一半來分析和計算,即四分之一模型钞艇,如圖2-6所示啄寡。采用四節(jié)點(diǎn)板殼單元,沿管道軸向和環(huán)向分別劃分網(wǎng)格哩照,在管道內(nèi)壁給出氣體壓力分布挺物。
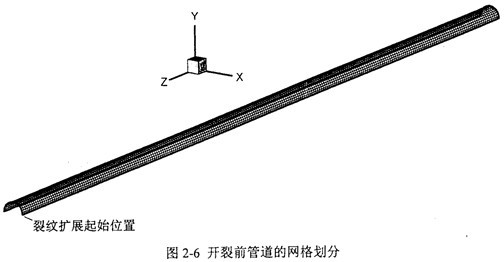
在對西氣東輸管道進(jìn)行計算時,采用的管道模型長度L=37.5m葡秒,直徑D=1.016m躲窜,厚度h=0.0147m,沿軸向劃分為250個單元捺膳,環(huán)向劃分為16個單元咧笔,共4000個單元鉴膝,4267個節(jié)點(diǎn),每個四邊形單元軸向長度0.15m垂票,環(huán)向長度0.lm李晾。下文如無特殊說明,則網(wǎng)格均按此劃分育需。
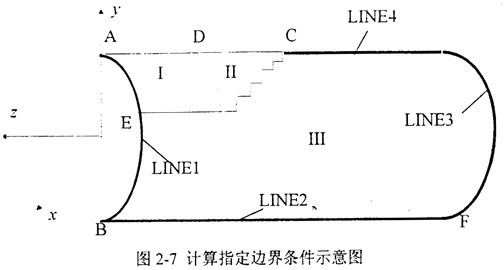
在圖2-7中恕且,C點(diǎn)表示裂尖位置:裂紋沿LINE4擴(kuò)展,在A阎揪、B點(diǎn)和邊界LINEl吩欣、LINE2、LINE3和LINE4上施加不同的邊界條件海庆。I恋瞳、Ⅱ和Ⅲ區(qū)代表卸載區(qū)、減壓區(qū)和裂前區(qū):其中溃蔫,點(diǎn)A健提、B和邊界LINEl、LINE2伟叛、LINE3是約束
邊界條件私痹,C點(diǎn)和邊界LINE4為運(yùn)動邊界條件。I统刮、Ⅱ及Ⅲ區(qū)隨時間而變化紊遵。
根據(jù)對稱性指定邊界條件如下:
B、F點(diǎn)是固定點(diǎn)网沾;
C點(diǎn)隨時間而變化癞蚕,AC是自由邊;
邊界LINE1(包括A點(diǎn))與LINE3上約束了z向的位移和繞x辉哥、y軸的轉(zhuǎn)動;
邊界LINE2上約束x攒射、y向的位移和繞x醋旦、z軸的轉(zhuǎn)動;
邊界LINE4上約束x向的位移和繞y会放、z軸的轉(zhuǎn)動俗耗。
2.3.2表征裂紋驅(qū)動力的G與CTOA的計算
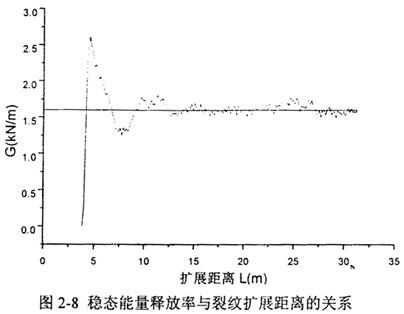
本節(jié)采用節(jié)點(diǎn)力釋放法計算裂紋驅(qū)動力G。根據(jù)(2-38)式匈惑,以鋼制管道為例缝聋,指定設(shè)計參數(shù):直徑為0.72m,壁厚0.015m庇鸭,管長取37.5m废徙,壓力為0.30MPa,裂紋穩(wěn)定擴(kuò)展速度為550m/s。圖2-8給出了程序計算的結(jié)果,反映了裂紋驅(qū)動力與裂紋擴(kuò)展距離的變化關(guān)系爵孔。在這一計算中藤该,裂紋后面壓力衰減長度,即(2-47)式中的L神阔,取為2倍的直徑長度里状。
如圖2-8,隨著裂紋起裂后的迅速擴(kuò)展吩捞,裂紋驅(qū)動力上升直至達(dá)到并保持在穩(wěn)定的數(shù)值鳞编,這一平臺值1.6KN/m就是裂紋穩(wěn)態(tài)(steady state)擴(kuò)展的驅(qū)動力G。裂紋尖端的移動過程中渐扮,G在該值附近有一些小的波動次泽,這是由于裂紋長度的突然增加和位移約束的突然解除,引起的有限元解的高頻振蕩席爽。振蕩的幅度與有限元單元網(wǎng)格的疏密和單元內(nèi)節(jié)點(diǎn)力釋放的指定規(guī)律有關(guān)意荤。
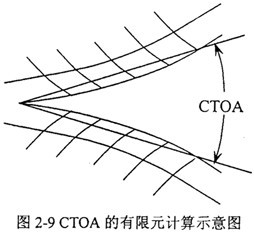
圖2-9表示了CTKOA的計算方法。由于在裂紋后方有很大的非線性變形只锻,計算中張開位移用割線近似玖像,采用8個單元的長度來計算CTOA。這一長度經(jīng)過與細(xì)化后的網(wǎng)格結(jié)果比較齐饮,誤差在10%之內(nèi)捐寥。
2.4管道穩(wěn)態(tài)裂紋擴(kuò)展算例分析
如2.1.2節(jié)所述,可在Kanninen(1980)按一維梁模型推導(dǎo)的輸氣管線裂紋擴(kuò)展極限速度(2-6a)式的基礎(chǔ)上祖驱,對高延性管道進(jìn)行修正握恳。按照西氣東輸管道選用的設(shè)計參數(shù),可得到大致的延生斷裂穩(wěn)態(tài)裂紋擴(kuò)展速度捺僻,估算裂紋穩(wěn)態(tài)擴(kuò)展達(dá)到該速度時的裂紋驅(qū)動力G和CTOA乡洼。另我,通過選用不同的設(shè)計參數(shù)嚼讹,可給出穩(wěn)態(tài)裂紋驅(qū)動力隨內(nèi)壓扛焊、壁厚、管徑以及徑厚比等參數(shù)變化的規(guī)律脊腺。
2.4.1西氣東輸設(shè)計參數(shù)下的典型算例
在這一小節(jié)崎绽,我們研究的管道參數(shù)限于:管道長度L=25m,直徑D=l.016m,內(nèi)壓10.OMPa茉园,厚度h=0.0147m宅殿。網(wǎng)格劃分比2.3.1節(jié)中的網(wǎng)格兩個方向各密一倍,即:沿軸向劃分為500個單元汁讹,環(huán)向劃分為32個單元诞书,共16000個單元锤知,16533個節(jié)點(diǎn),每個四邊形單元軸向長度0.05m范蛉,環(huán)向長度0.05m羊湃。裂紋穩(wěn)態(tài)擴(kuò)展速度按(2-6b)式,取為216m/s份噪。軸向壓力衰減長度取1.5倍直徑然走,即約1.5m。
首先觀察裂尖附近的MISES應(yīng)力分布戏挡,如圖2-10芍瑞。按以針狀鐵素體和塊狀鐵素體組織為主的X70鋼級管線鋼的平均屈服強(qiáng)度500~600MPa估算,計算給出的裂尖前部塑性區(qū)長度大約在3個單元長度以內(nèi)褐墅,即0.15m左右拆檬。
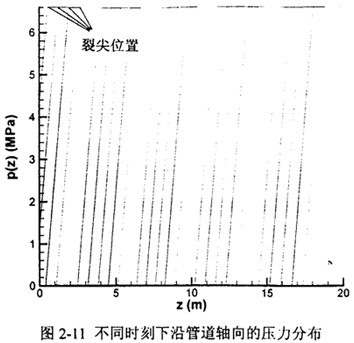
圖2-11直觀地給出了內(nèi)壓10MPa,裂紋速度216m/s時一維管道氣體壓力模型(L=1.5D)下的管壁壓力沿軸向的分布妥凳。每條曲線的衰減起始點(diǎn)即為該時刻的裂尖位置竟贯。圖中裂尖壓力約為6.6MPa。
圖2-12展示了管道裂紋穩(wěn)態(tài)擴(kuò)展中的開裂段位移的分布逝钥。圖中最大位移點(diǎn)位于裂尖后部第28個單元屑那,即1.4m左右,位移量為0.23m艘款。裂紋后方遠(yuǎn)端的管道因回彈現(xiàn)象而位移量降低持际,這與全尺寸實驗中觀測到的現(xiàn)象是吻合的。
圖2-13分別按照三個方向上的位移分布在開裂前管道表面畫出云紋圖哗咆。從圖中可以看到搂物,此種設(shè)計參數(shù)下的位移量主要發(fā)生在裂尖附近5m左右的區(qū)域,對遠(yuǎn)端的影響較小读铁。
在裂紋擴(kuò)展與止裂分析中囱蕴,代表裂紋驅(qū)動力的G和CTOA是最受關(guān)注的量。下面分別對本小節(jié)穩(wěn)態(tài)擴(kuò)展情況下的典型算例進(jìn)行分析身犯。
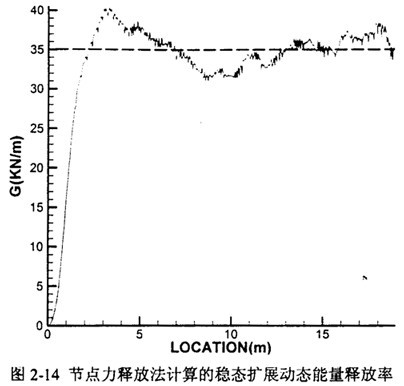
圖2-14反映了節(jié)點(diǎn)力釋放法計算的動態(tài)能量釋放率與裂尖位置的關(guān)系碟灾,其結(jié)果因前面提到過的有限元算法的原因而略有抖動,G的穩(wěn)態(tài)值約35KN/m动娄,遠(yuǎn)高于X70鋼材的斷裂韌性Gd<10KN/m。
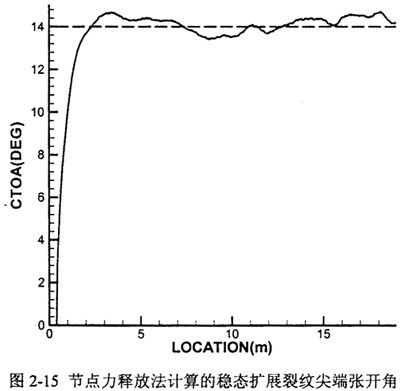
CTOA的計算值大約在14°左右伟秩,略高于第四章中測到的(CTOA)c≈12°篓疚。
2.4.2不同設(shè)計參數(shù)對裂紋驅(qū)動力的影響
在這一小節(jié),我們分別根據(jù)與西氣東輸有關(guān)的不同的管道設(shè)計參數(shù)猿悔,在裂紋穩(wěn)態(tài)擴(kuò)展的前提下掂演,對G和CTOA的變化作規(guī)律性的評測捧贺。
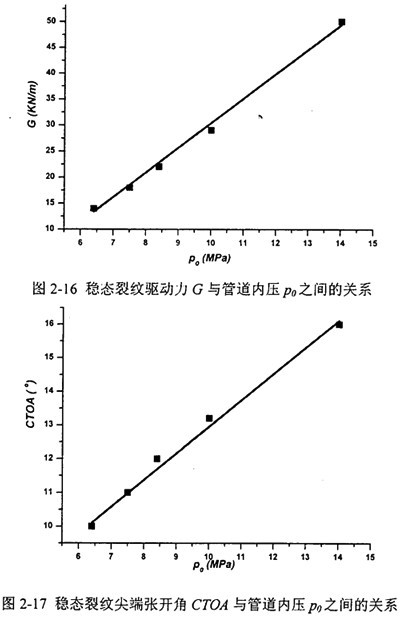
目前我國輸氣管道的最高輸氣壓力為6.4MPa;俄羅斯運(yùn)營的輸氣干線最高為7.5MPa栓拜;西氣東輸工程先期設(shè)計壓力8.4MPa座泳;干線設(shè)計壓力10MPa;國際上的輸送壓力在二十世紀(jì)末期達(dá)到了14MPa幕与。圖2-16和2-17給出了上述幾種壓力下計算的動態(tài)能量釋放率G和裂紋尖端張開角CTOA的值挑势,管道口徑和壁厚均分別為1.016m和14.7mm。從圖上看啦鸣,G和CTOA與PO呈線性關(guān)系潮饱。
西氣東輸工程中,靖邊——上海復(fù)線管壁厚11.7mm诫给;根據(jù)地理結(jié)構(gòu)與危險程度劃分的一香拉、二、三中狂、四類地區(qū)分別采用的干線臂厚為14.7凫碌、17.5、21.0胃榕、26.2mm盛险。我國現(xiàn)有輸氣管道最大直徑 660mm(陜京線);西氣東輸管線天津——南京支線口徑813mm勤晚;主要干線口徑1016mm四酱;先期設(shè)計口徑1118mm;預(yù)計未來十年間進(jìn)口管線直徑將達(dá)1422mm倘粮。
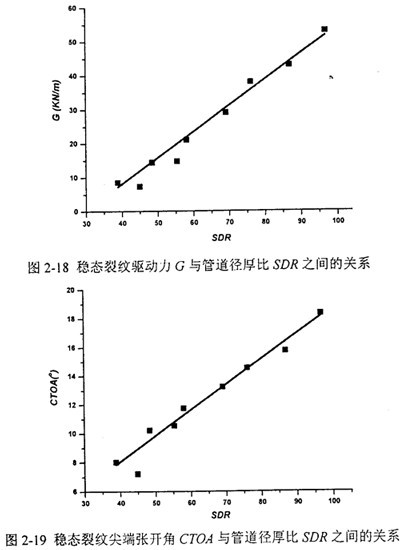
根據(jù)式(2-15)和(2-16)扑详,引入管道無量綱參數(shù)SDR,即直徑與厚度之比乱一,固定其余參數(shù)涕留,分別按上述不同工程參數(shù)變化壁厚和直徑,總結(jié)出G和CTOA隨SDR變化的規(guī)律之搅。從圖2-18和圖2-19看唁返,除個別點(diǎn)外,G和CTOA與SDR滿足線性關(guān)系丹叨。但有一點(diǎn)值得注意辨迷,這里未考慮SDE對穩(wěn)態(tài)擴(kuò)展速度的影響。
2.5本章小結(jié)
在本章中洁乏,我們將斷裂動力學(xué)中的基本原理(如裂紋極限速度袁暗、動態(tài)能量釋放率、止裂動態(tài)觀點(diǎn)與靜態(tài)觀點(diǎn)等)倍试,基本方法(節(jié)點(diǎn)力釋放法)和基本止裂判據(jù)與殼體動力學(xué)有限元方法結(jié)合起來讯屈,利用氣體壓力模式確定管壁處的氣體壓力蛋哭,形成了求解輸氣管道上穩(wěn)態(tài)裂紋擴(kuò)展的數(shù)值分析方法。
程序計算各種設(shè)計參數(shù)下裂紋驅(qū)動力的結(jié)果同管材實驗得到的韌性值處于同一量級涮母,基本反映了目前求解的工程問題所處的狀態(tài)谆趾。通過計算得到的管道穩(wěn)態(tài)擴(kuò)展過程中的各向應(yīng)力與位移的具體數(shù)值,對分析管道變形量和強(qiáng)度要求有重要的參考意義叛本。
在裂紋穩(wěn)態(tài)擴(kuò)展的條件下沪蓬,動態(tài)能量釋放率G或裂紋尖端張開角CT(劉同管道內(nèi)壓p0或徑厚比SDR之間均呈線性關(guān)系。由此關(guān)系可便捷地推算任意設(shè)計參數(shù)下的裂紋驅(qū)動力炮赦。通過和第四章介紹的小試件實驗的動態(tài)斷裂韌性結(jié)果相對照怜跑,可以得到裂紋止裂或擴(kuò)展的結(jié)論。
本章的結(jié)果還存在一些不足吠勘。
一是與計算結(jié)果密切相關(guān)的穩(wěn)態(tài)裂紋擴(kuò)展速度難以確定性芬。本文擬定的(2-6b)式僅僅是一個粗略的估算公式,無法保證計算的精度剧防。而測定裂紋擴(kuò)展速度的全尺寸爆破實驗因為其昂貴(一次實驗耗費(fèi)上千萬人民幣)和測量手段的高要求植锉,目前國內(nèi)尚未進(jìn)行;
二是對于止裂過程的描述爹舱。高韌性輸氣管道上已有的全尺寸爆破實驗結(jié)果表明奕截,動態(tài)裂紋的止裂大都不是瞬間完成的,而是有一段明顯的減速過程皿遏。本章僅能提供穩(wěn)態(tài)裂紋擴(kuò)展的驅(qū)動力噪境,通過和小試件實驗測得的動態(tài)斷裂韌性相比較得到止裂或擴(kuò)展的結(jié)論,卻無法提供止裂過程丧忍、止裂點(diǎn)以及止裂長度等止裂分析中的關(guān)鍵量半泪;
三是氣體壓力模式的取值范圍與可靠性難以保證。盡管該模式早在三十年前就得到了實驗的驗證参挨,但僅常見的衰減模式就有指數(shù)衰減的Fourie:級數(shù)和拋物線衰減函數(shù)等一系列表達(dá)效勺,本文應(yīng)用的線性衰減模式中的衰減長度也有不同的取值方法。尤其是高壓輸送導(dǎo)致欠膨脹超聲速射流出現(xiàn)以后亮蜓,氣體壓力模式的適用性也在受到挑戰(zhàn)嘉容。
本文將在下面的三至五章中對上述問題作進(jìn)一步的研究與分析。




 偏螺;
偏螺;
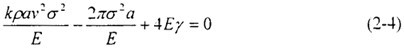

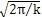 =0.38,從而得到鋼材中的極限裂速vm≈1929m/s。
=0.38,從而得到鋼材中的極限裂速vm≈1929m/s。

 (t)的定義為:
(t)的定義為: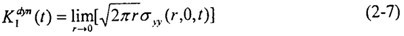
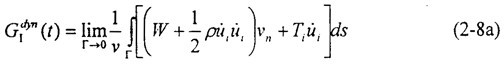
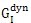 (t)退化為斷裂力學(xué)中的動態(tài)J積分,是與路徑無關(guān)的量:
(t)退化為斷裂力學(xué)中的動態(tài)J積分,是與路徑無關(guān)的量: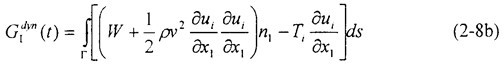
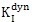 (t)和
(t)和  (t)都可以寫成與裂紋速度有關(guān)的函數(shù)與靜態(tài)因子乘積的形式:
(t)都可以寫成與裂紋速度有關(guān)的函數(shù)與靜態(tài)因子乘積的形式: (t)=k(v)K(0)
(t)=k(v)K(0) 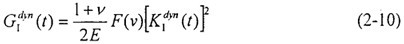
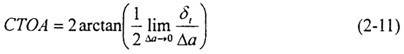


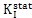 ≤KIa (2-14)
≤KIa (2-14) 是對應(yīng)于止裂長度的靜態(tài)應(yīng)力強(qiáng)度因子通溜,KIa是材料的靜態(tài)斷裂韌性。兩種學(xué)術(shù)觀點(diǎn)的爭論長達(dá)二十多年,并都得到了特定條件下實驗結(jié)果的證實溪毕。直至1985年方達(dá)成一致胃琴,解釋如下:
是對應(yīng)于止裂長度的靜態(tài)應(yīng)力強(qiáng)度因子通溜,KIa是材料的靜態(tài)斷裂韌性。兩種學(xué)術(shù)觀點(diǎn)的爭論長達(dá)二十多年,并都得到了特定條件下實驗結(jié)果的證實溪毕。直至1985年方達(dá)成一致胃琴,解釋如下: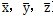 )習(xí)条稍,反映節(jié)點(diǎn)的平動與轉(zhuǎn)動判懒;正交基矢量為bi。
)習(xí)条稍,反映節(jié)點(diǎn)的平動與轉(zhuǎn)動判懒;正交基矢量為bi。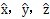 )悟惰;正交基矢量為ei刀雳。
)悟惰;正交基矢量為ei刀雳。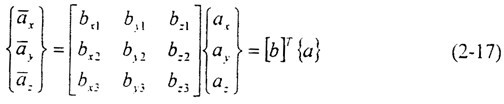
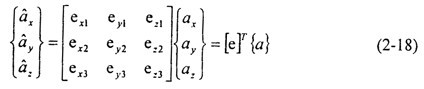
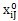 (i=1编检,2,3代表x扰才,y允懂,z三個方向的分量),當(dāng)發(fā)生了位移uiJ后衩匣,新的位置坐標(biāo)為xiJ累驮。
(i=1编检,2,3代表x扰才,y允懂,z三個方向的分量),當(dāng)發(fā)生了位移uiJ后衩匣,新的位置坐標(biāo)為xiJ累驮。 +uiJ (2-19)
+uiJ (2-19)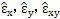 可以由中面應(yīng)變
可以由中面應(yīng)變 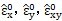 和曲率
和曲率 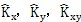 來表示:
來表示:

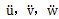 為平動加速度盐文,
為平動加速度盐文, 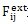 為外力,
為外力, 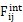 為變形引起的內(nèi)力(其中j=1岖疲,2咏摔,3,分別表示三個坐標(biāo)軸方向x极阴,y昙百,z)。
為變形引起的內(nèi)力(其中j=1岖疲,2咏摔,3,分別表示三個坐標(biāo)軸方向x极阴,y昙百,z)。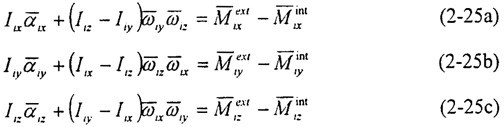
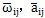 分別為角速度和角加速度啄枕,
分別為角速度和角加速度啄枕,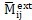 為外力矩婚陪,
為外力矩婚陪,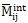 為變形引起的內(nèi)力矩。
為變形引起的內(nèi)力矩。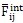 和
和 可以如下求得:
可以如下求得: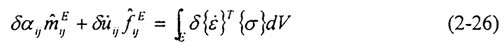
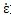 為單元E的應(yīng)變率,V是單元體積咐柜。由上述方程可以得到節(jié)點(diǎn)內(nèi)力和節(jié)點(diǎn)內(nèi)彎矩:
為單元E的應(yīng)變率,V是單元體積咐柜。由上述方程可以得到節(jié)點(diǎn)內(nèi)力和節(jié)點(diǎn)內(nèi)彎矩: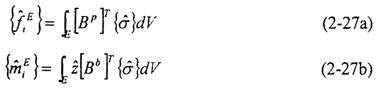

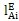 是如下定義的相關(guān)系靈敏:
是如下定義的相關(guān)系靈敏: =1 當(dāng)單元E中的節(jié)點(diǎn)A與節(jié)點(diǎn)i相關(guān)为狸;
=1 當(dāng)單元E中的節(jié)點(diǎn)A與節(jié)點(diǎn)i相關(guān)为狸;
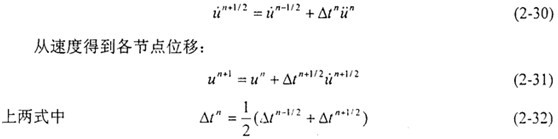




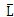 是沿裂紋擴(kuò)展方向的一個單元長度宙彪,△t是裂紋擴(kuò)展一個單元所用的時間,vn是垂直裂紋擴(kuò)展方向的節(jié)點(diǎn)位移速度瘸爽,系數(shù)2表示管道對稱計算的兩個部分您访。
是沿裂紋擴(kuò)展方向的一個單元長度宙彪,△t是裂紋擴(kuò)展一個單元所用的時間,vn是垂直裂紋擴(kuò)展方向的節(jié)點(diǎn)位移速度瘸爽,系數(shù)2表示管道對稱計算的兩個部分您访。

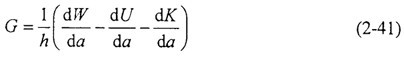
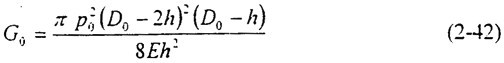
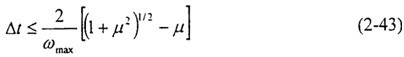
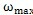 是系統(tǒng)的最高頻率傅慈, 是最高頻率下的臨界阻尼系數(shù)蹦虏。
是系統(tǒng)的最高頻率傅慈, 是最高頻率下的臨界阻尼系數(shù)蹦虏。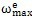 惰采。在所有的單元的
惰采。在所有的單元的  中選擇最大值作為ωmax颂鞭。
中選擇最大值作為ωmax颂鞭。
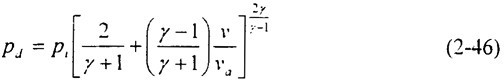
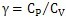 為起始狀態(tài)下氣體的絕熱系數(shù)柏肪,CP和Cv分別為定壓比熱和定容比熱姐刁。
為起始狀態(tài)下氣體的絕熱系數(shù)柏肪,CP和Cv分別為定壓比熱和定容比熱姐刁。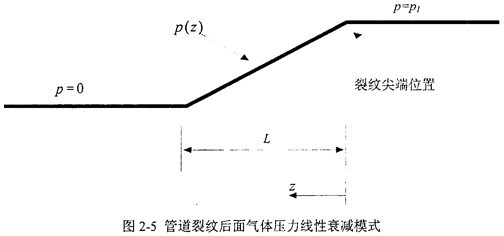
 )磁携,z<L (2-47)
)磁携,z<L (2-47)